solução da primeira prova - Instituto de Física / UFRJ

Tópicos de Física Básica
2006/1 – prof. Marta
SEMANA 8 – PRIMEIRA PROVA - SOLUÇÃO
NOME: _____________________________________________________________________
TÓPICOS DE FÍSICA BÁSICA – 2006/1 – Turma IFA
PRIMEIRA PROVA – SOLUÇÃO
QUESTÃO 1 (valor: 1,5 pontos)
Numa experiência, foram determinados os valores da velocidade de um corpo que se move sobre
uma linha reta em função do tempo. O gráfico abaixo indica os resultados obtidos.
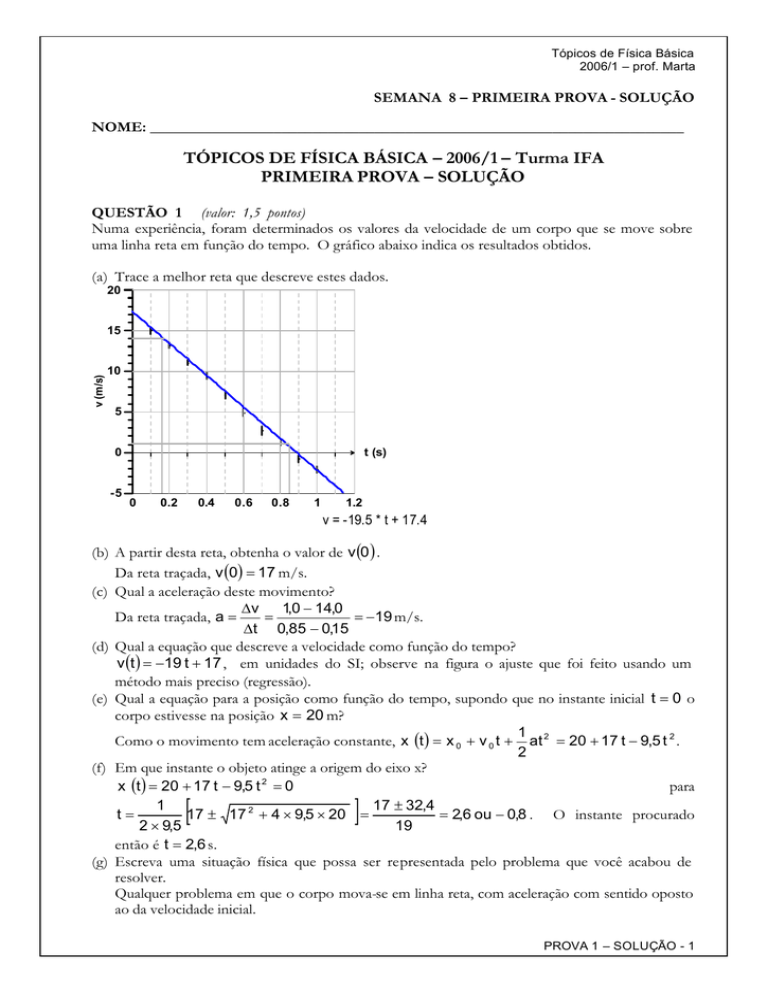
(a) Trace a melhor reta que descreve estes dados.
20
v (m/s)
15
10
5
0
-5
t (s)
0
0.2
0.4
0.6
0.8
1
1.2
v = -19.5 * t + 17.4
(b) A partir desta reta, obtenha o valor de v (0 ) .
Da reta traçada, v (0) = 17 m/s.
(c) Qual a aceleração deste movimento?
∆v
1,0 − 14,0
Da reta traçada, a =
=
= −19 m/s.
∆t 0,85 − 0,15
(d) Qual a equação que descreve a velocidade como função do tempo?
v (t) = −19 t + 17 , em unidades do SI; observe na figura o ajuste que foi feito usando um
método mais preciso (regressão).
(e) Qual a equação para a posição como função do tempo, supondo que no instante inicial t = 0 o
corpo estivesse na posição x = 20 m?
1
Como o movimento tem aceleração constante, x (t ) = x 0 + v 0 t + at 2 = 20 + 17 t − 9,5 t 2 .
2
(f) Em que instante o objeto atinge a origem do eixo x?
x (t ) = 20 + 17 t − 9,5 t 2 = 0
para
1
17 ± 32,4
t=
17 ± 17 2 + 4 × 9,5 × 20 =
= 2,6 ou − 0,8 . O instante procurado
2 × 9,5
19
então é t = 2,6 s.
(g) Escreva uma situação física que possa ser representada pelo problema que você acabou de
resolver.
Qualquer problema em que o corpo mova-se em linha reta, com aceleração com sentido oposto
ao da velocidade inicial.
[
]
PROVA 1 – SOLUÇÃO - 1
Tópicos de Física Básica
2006/1 – prof. Marta
QUESTÃO 2 (valor: 1,5 pontos)
Um jogador de basquete quer encestar a bola lançando-a de uma altura de 2 m do chão com
velocidade inicial de 7 m/s. A distância da bola à vertical que passa pelo centro do cesto é de 3 m, e
o aro do cesto está a 3,05 m de altura do chão.
(a) Desenhe a situação descrita.
y
r
v0
θ
H
h
x
D
(b) Escolha um sistema de coordenadas cartesianas para resolver o problema, desenhe-o na figura e
escreva as coordenadas cartesianas que descrevem a posição da bola como função do tempo
supondo que a bola é lançada com uma velocidade que faz um ângulo θ com a horizontal.
O sistema de coordenadas está desenhado na figura; o movimento da bola (partícula) é
descrito por:
x( t ) = v ο cos θ t ;
v x ( t ) = v ο cos θ ; a x ( t ) = 0
1
y( t ) = h + v ο senθ t − g t 2 ;
v y ( t ) = v ο senθ − g t ; a y ( t ) = − g
2
v ο cos θ
(c) Obtenha o valor do ângulo de lançamento.
Para que a bola atinja a cesta, é necessário que y( x = D ) = H . Podemos escrever a equação
x
da trajetória substituindo t =
na expressão para y(t ) :
v ο cos θ
y( t ) = h + v ο senθ
g
x
1
x2
− g 2
= h + tg θ x −
sec 2 θ x 2
2
2
v ο cos θ 2 v ο cos θ
2v ο
Lembrando que sec 2 θ = 1 + tg 2 θ e considerando o ponto em que a bola atinge a cesta,
g
H = h + tg θ D −
1 + tg 2 θ D 2 ou a equação de segundo grau para tg θ :
2
2v ο
(
g D2
2v
2
ο
)

g D2 

=0
tg θ − D tg θ +  H − h +
2 
2
v

ο 
2
ou
0,9 tg 2 θ − 3 tg θ + (1,05 + 0,9 ) = 0
Então
3 ± 9 − 4 × 0,9 × 1,95 3 ± 2
=
= 2,8 ou 0,6
2 × 0,9
1,8
e θ = arctg 2,8 = 70° ou θ = arctg 0,6 = 31° . Para o primeiro ângulo ( 70° ) é mais
certo que a bola entre na cesta (sem ficar no aro).
tg θ =
PROVA 1 – SOLUÇÃO - 2
Tópicos de Física Básica
2006/1 – prof. Marta
QUESTÃO 3 (valor: 1,5 pontos)
Um livro de massa m é pressionado contra uma parede vertical com uma força horizontal de
módulo F igual ao peso de uma massa de 0,3 kg. São determinados experimentalmente os melhores
valores para os coeficientes de atrito estático µ E = 0,4 e cinético µ C = 0,3 entre as superfícies do
livro e da parede. (a) Faça um desenho da situação descrita. (b) Faça o diagrama das forças que atua
sobre o livro. (c) Se a massa do corpo for m = 0,2 kg, o que acontece – o livro fica parado ou
desliza? Se desliza, com que aceleração? Por quê? (d) Se a massa do corpo for m = 0,8 kg, o que
acontece – o livro fica parado ou desliza? Se desliza, com que aceleração? Por quê? (e) Qual o
maior valor da massa do livro para que a pressão consiga impedir que ele deslize pela parede e caia?
(a)
(b)
r
F
r
F
r
N
r
fa
r
P
r
As forças que atuam sobre o corpo são a força F (de módulo igual a F = 3 N ) , a força peso
r
r
r
P = m g , resultante da interação gravitacional com a Terra, e as duas componentes normal N e
r
atrito f a da força de contato entre a superfície do bloco e a da parede. Aplicando a segunda lei de
r
r r r
r
Newton ao livro, escrevemos F + m g + N + f a = m a .
Como na horizontal (perpendicular à parede) não há movimento, podemos escrever
F = N = 3 N.
(c) Na vertical, considerando o sentido positivo para baixo, temos mg − f a = ma .
Se a massa do corpo for m = 0,2 kg, seu peso é P = 2 N.
Se o atrito for estático, sabemos (fenomenologicamente) que
f EST ≤ µ E N = 0,4 × 3 = 1,2 N.
Logo, o atrito estático máximo é menor que o peso do objeto, e portanto ele desliza. Como há
deslizamento, o atrito é cinético,
f CIN ≤ µ CN = 0,3 × 3 = 0,9 e aceleração do livro é
a = (2,0 − 0,9) 0,2 = 5,5 m / s 2 para baixo.
(d) Se a massa do corpo for m = 0,8 kg, o peso é de 8N e o corpo desliza para baixo com aceleração
a = (8,0 − 0,3 × 3 ) 0,8 = 8,9 m / s 2 .
(e) Para que o livro não deslize, é necessário que m g ≤ µ E N ; no caso,
m ≤ (µ E N) g = (µ E F) g = (0,4 × 3) 10 = 0,12 kg.
PROVA 1 – SOLUÇÃO - 3
Tópicos de Física Básica
2006/1 – prof. Marta
QUESTÃO 4 (valor: 1,5 pontos)
Queremos descobrir quanto vale a força resultante que age sobre um objeto de massa m que
descreve um movimento circular uniforme de raio R e período T . Apresentamos a seguir uma
argumentação escrita, e você deve transformá-la em linguagem matemática. Deve tam-bém justificar
as passagens feitas; se eventualmente houver algum espaço vazio, você deve preenchê-lo.
O corpo descreve um círculo de raio R . Num intervalo de tempo ∆t pequeno, ele percorre
r
um ângulo ∆θ . O seu deslocamento corresponde ao vetor ∆ r da figura (desenhe-o). Se o
ângulo for pequeno, o arco de circunferência se confunde com o segmento de reta
representado pelo vetor.
r
∆r
ω
∆θ
ω
∆θ
r
∆s ≅ ∆ r
Podemos escrever que a velocidade, em módulo, é igual ao deslocamento dividido pelo tempo,
no limite em que o intervalo de tempo vai a zero (ou a taxa de variação da posição com o
tempo, ou a derivada da posição em relação ao tempo).
r
r
∆r
r
dr
v = lim
=
∆t →0 ∆t
dt
O módulo do deslocamento tem o tamanho do arco de circunferência: vale o ângulo
r
r
∆ r ≅ ∆s = r ∆θ = R ∆θ
∆θ
vezes
R , quando ∆θ é pequeno.
Chamando ω a velocidade angular (ângulo percorrido por intervalo de tempo) podemos
o raio
escrever que o módulo da velocidade vale
r
∆r
r
R ∆θ
∆θ
dθ
v = lim
= lim
= R lim
=R
= ωR ⇒ v = ωR
∆ t → 0 ∆t
∆ t → 0 ∆t
∆t → 0 ∆t
dt
e que a velocidade tem a direção perpendicular ao raio.
Usando coordenadas polares planas e os unitários da figura e o resultado anterior podemos
escrever que
θ̂
r
v = ω R θˆ .
r̂
r
r
d θˆ
= − ω r̂ (ou seja, que o vetor unitário θ̂ está girando a
dt
r
uma taxa bem determinada), podemos calcular a aceleração a do corpo no caso em que o
Lembrando que
movimento circular é uniforme de maneira simples.
r
r dv d
d θˆ
a=
=
ω R θˆ = ω R
= − ω 2 R r̂
dt dt
dt
(
Calcule-a.
)
A seguir, trace uma figura do movimento e desenhe o vetor força
Qual o valor da velocidade angular (em função dos dados do problema, R e T ).
r
v
r
FR
resultante.
ω
ω = ∆θ ∆t = 2 π T
PROVA 1 – SOLUÇÃO - 4
Tópicos de Física Básica
2006/1 – prof. Marta
QUESTÃO 5
(valor: 1,5 pontos)
B
r
u
C
A
Considere um rio cujas águas têm velocidade de módulo u como mostrado na figura. A distância
entre os pontos A e C é D , e a distância entre os pontos A e B também é D . Você rema com
velocidade de módulo v em relação à água.
(a) Você vai remando do ponto A até o ponto C e retorna ao ponto A. Calcule, no caminho, a
velocidade do barco em relação a um observador fixo à Terra tanto na ida quanto na volta.
Calcule o tempo de percurso.
(b) Você rema do ponto A até o ponto B. Calcule (e desenhe) a velocidade do barco em relação à
Terra no caminho de ida e no caminho de volta. Obtenha o tempo de percurso.
r
r r
(a) Visto da Terra, VB = v + u . As situações da ida e volta estão representadas abaixo.
B
B
r
v
r
VB
A
ida
r
VB
r
v
r
u
C
t AC =
A
volta
VB = v + u
ida:
volta:
D
D
=
Vb v + u
r
u
C
VB = v − u
t CA =
D
D
=
Vb v − u
2 vD
D
D
+
= 2
v + u v − u v − u2
(b) As situações da ida e da volta estão representadas nas figuras abaixo.
TACA = t AC + t CA =
B
r
VB
A
B
r
v
r
VB
r
u
r
v
A
C
Na ida e na volta, v 2 = VB 2 + u 2
t AB = t BA =
r
u
D
=
Vb
D
v 2 − u2
C
⇒
VB = v 2 − u 2
e
TABA =
2D
v 2 − u2
PROVA 1 – SOLUÇÃO - 5
Tópicos de Física Básica
2006/1 – prof. Marta
QUESTÃO 6 (valor: 1,0 pontos)
Um objeto de massa m – um pêndulo simples – está preso por um fio de comprimento L ao teto de
uma sala.
(a) Faça um diagrama das forças que atuam sobre o objeto num instante qualquer de sua trajetória.
(b) Por que você pode usar a conservação da energia entre dois pontos quaisquer da trajetória do
corpo?
(c) Se o corpo é lançado com o fio fazendo um ângulo de 60° com a vertical, qual a maior
velocidade do corpo?
(a)
r
T
r
P
(b) A força peso é conservativa, e a tração não realiza trabalho (está sempre na direção do fio).
Logo, a energia é conservada.
(c) Se a energia se conserva, a energia cinética somada à potencial é constante. O menor valor da
energia potencial ocorre no ponto mais baixo da trajetória (fio na vertical). No instante inicial,
2
E = m g h = mg (L − L cos θ) = m g L / 2 , e no ponto mais baixo da trajetória, E = m v MAX
/2.
Portanto,
m g L / 2 = m v 2MAX / 2 ⇒ v MAX = g L
QUESTÃO 7 (valor: 0,5 pontos)
Escreva as três leis de Newton.
Procure no livro texto de Física 1.
PROVA 1 – SOLUÇÃO - 6