Exercícios Teórico-Práticas - Moodle

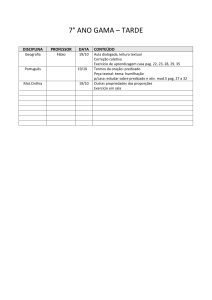
Teoria da Computação
2013/2014
Exercícios
1
Máquinas de Registos Ilimitados
1. Construa programas URM sem módulos que calculem as seguintes funções
(a)
(b)
(c)
(d)
(e)
(f )
(g)
(h)
(i)
(j)
quatro(x) = 4
sg(x) retorna 0 se x > 0, 1 no caso contrário
halfd(x) devolve metade de x se x for par, diverge se x for ímpar
max(x, y) devolve o máximo dos dois argumentos
qt(x, y) devolve o quociente da divisão inteira de x por y
raiz(x) devolve a raiz quadrada de x se x é um quadrado perfeito, diverge caso contrário
A função característica do predicado x é igual a 2 A função característica do predicado x é maior que y A função característica do predicado o resto da divisão de x por 3 é 1 A função característica do predicado x é quadrado perfeito 2. Construa programas URM para calcular as funções com assinatura
(a)
f (x) = −x
(b)
f (x) = −2x
(c) A função característica de x
< 0
(d) A função característica de x
é ímpar Z←Z
3. Utilizando os programas que fez como módulos, construa programas URM que calculem as
seguintes funções
(a)
f (x, y, z) = x + y + z
(b)
f (x, y, z) = max(x, y) + z
(c) Função característica do predicado
x é primo
(d) Função característica do predicado
x é cubo perfeito
(e)
p(x)
devolve o
x-ésimo
primo
4. Faça a expansão dos seguintes programas com módulos
(a) Considere que o programa tem dois argumentos.

J(1, 2, 4)
Soma[1, 2 → 1]


 J(1, 1, 5) 
Dois[→ 1]

(b) Considere que o programa tem dois argumentos.

J(1, 2, 4)
Xyz =  Foo[→ 1] 
Abc[1, 2 → 1]


S(1)
Foo = S(1)
S(1)


Z(2)
 S(3) 

Abc = 
J(1, 3, 1)
T(2, 1)

5. Codique os seguintes programas URM. Seguem algumas funções úteis. Codicação de
Π:
Inversas de
N2 :
N2
→ N
(m, n) 7→ 2n (2m + 1) − 1
Π:
Π1 : N
x
→
7→
expoente do número 2 na factorização prima de
Π2 : N
x
N
(x + 1)1
x.
→ N
1 x+1
(
− 1)
7→
2 2Π1 (x)
(a)
Soma = [J(3, 2, 5), S(1), S(3), J(1, 1, 1)]
(b)
Eq = [J(1, 2, 4), Z(1), J(1, 1, 6), Z(1), S(1)]
6. Encontre os programas que estão associados aos números
(a)
dec(64)
(b)
dec(256)
(c)
dec(225)
(d)
dec(523)
7. O modelo URM pode ser denido unicamente à custa das instruções
(a) Como programaria a instrução
T(n, m)
Z(n), S(n) e J(n, m, q).
usando as três instruções anteriores?
(b) Como caria a codicação de programas URM restritos a estas três instruções?
Soma = [J(3, 2, 5), S(1), S(3), J(1, 1, 1)]. Apresente 3 conjuntos de
N. Sugestão: considere suxos ao programa
unicamente por instruções Z(n), S(n) e T(n, m).
8. Considere o programa
programas de cardinalidade igual ao conjunto
Soma
compostos
Page 2
2
Funções Parciais Recursivas
1. Considere as seguintes funções
f : N2 → N g : N3 → N h : N4 → N
Diga para cada uma das expressões seguintes se estão correctas e se sim qual a aridade
(número de argumentos) da expressão resultante.
(a)
C[g; P12 , P22 , P12 ]
(b)
C[f ; P12 , P22 , P12 ]
(c)
C[h; P14 , P13 , P12 ]
(d)
R[f ; h]
(e)
R[2; f ]
(f )
R[g; P35 ]
(g)
(h)
(i)
R[P12 ; g]
P
z<y f (x, y)
P
z<y f (x, y)
2. Prove por via axiomática, a computabilidade das seguintes funções:
(a)
quatro(x) = 4
(b)
dobro(x) = 2x
(c)
triplo(x) = 3x
(d)
exp2(x) = x2
(e)
exp(x, y) = xy
(f )
max(x, y)
(g)
sg(x)
(h)
halfd(x)
devolve o máximo dos dois argumentos
retorna 0 se
x > 0,
1 no caso contrário
devolve metade de
x
se
x
for par, diverge se
x
for ímpar
(i)
qt(x, y)
(j)
raiz(x) devolve a raiz quadrada de x se x é um quadrado perfeito, diverge caso contrário
devolve o quociente da divisão inteira de
(k) A função característica do predicado
(l)
(x)1
x
por
y
x é quadrado perfeito
retorna o valor do primeiro expoente da expansão prima de
x.
de um número é igual ao produto de potências de números primos:
(m)
(n)
D(x),
devolve o número de divisores de
primo(x),
x.
função característica do predicado
(o) A função característica do predicado
x > y.
(p) A função característica do predicado
x|y ,
x é número primo.
ou seja
3. Para cada uma das funções seguintes obtenha o
Page 3
x
é divisor de
y.
A expansão prima
2x 3y 5z · · · .
3
Indecibilidade
1. Considere um alfabeto
A = {a1 , a2 , . . . , an }.
(a) Apresente uma função computável que codique
A? .
(b) Apresente uma função computável que descodique
2. Sejam
LA
e
LB
A? .
linguagens recursivas. Prove as seguintes armações:
(a)
LA
(b)
LA ∪ LB
é uma linguagem recursiva
(c)
LA ∩ LB
é uma linguagem recursiva
(d)
LA \ LB
é uma linguagem recursiva
é uma linguagem recursiva
3. Prove que as seguintes linguagens são decidíveis:
(a)
LA AF D = {hM, ui|M
é um AFD e aceita
u}
(b)
LV
AF D
= {hM i|M
é um AFD
∧ L(M ) = ∅}
4. Prove a indecibilidade das seguintes linguagens:
(a) Linguagem da aceitação
LA = {hM, ui|M
aceita
u}
(b) Linguagem da paragem
LH = {hM, ui|M termina
comu}
(c) Conjunto das linguagens que reconhecem linguagens regulares.
LR = hM i|M
gera uma linguagem regular
(d) Conjunto das linguagens que reconhecem linguagens independentes de contexto.
LIC = hM i|M
gera uma linguagem independente de contexto
(e) Conjunto das linguagens que reconhecem uma palavra e a sua inversa.
LP 1 = hM i|w ∈ L(M ) ⇔ wR ∈ L(M )
wR
representa a palavra
w
invertida.
5. Considere o problema em que as instâncias representam triplos
programa URM,
u
um argumento do argumento e
i
tâncias positivas são os triplos em que o programa executa a
considera-se que a computação
P (u)
u
em que
i-ésima
P
P.
instrução. Se
é um
As ins-
i > |P |
termina. Mostre que este problema é indecidível.
6. Considere o problema em que as instâncias representam tuplos
programa URM,
(P, u, i)
um índice de instrução de
um argumento do argumento,
r
(P, u, r, v)
em que
um índice de registo e
v
P
é um
um número
natural. As instâncias positivas são os triplos em que durante a computação do programa
ou após o seu término o registo
r
tem o valor
v.
Page 4
Mostre que este problema é indecidível.
7. Considere o modelo de computação R1 URM que representa uma restrição do modelo URM
em que os registos só têm
k -bits.
(a) Mostre que a linguagem da aceitação restrita a este modelo é decidível.
LA R1 U RM = hP, ui|P
é um R1 URM
∧ P (u) ↓ 1
(b) Mostre que a linguagem vazio restrita a este modelo é decidível.
LV
R1 U RM
= {hP i|L(P ) = ∅}
8. Mostre que o problema da Correspondência de Post restrito ao alfabeto
4
{0}
é decidível.
Complexidade
1. Dê uma denição para a relação ser
(a)
2
1/2n − 3n
3
é
6n
(c)
(n + a)b
(d)
n2 − 100000n
(e)
200n2 + n
é
de e mostre que
O(n )
O(n2 )
(b)
não é
O
2
O(nb )
é
não é
O(n)
O(n2 )
2. De um modo geral, para podermos tratar computacionalmente um problema temos que converter instâncias de um problema em números naturais. É preciso uma função que codique
instâncias em números naturais
f : I 7→ N
(a) Apresente uma função que codique instâncias do problema
3SAT .
Uma instância
representa conjuntos nitos de cláusulas com três literais.
(b) Apresente uma função que codique instâncias do problema
CF C .
Uma instância re-
SAT .
Uma instância re-
presenta conjuntos nitos de cláusulas.
(c) Apresente uma função que codique instâncias do problema
presenta uma fórmula conjuntiva.
(d) Apresente uma função que codique instâncias do problema
um par
(G, k)
em que
G
é um grafo e
k
COBV .
Uma instância é
um número natural.
3. Para cada um dos seguintes problemas mostre que pertencem à classe
NP.
(a) Uma clique é um grafo não direccionado em que todos os vértices estão ligados a todos
os outros. Um grafo pode conter um sub-grafo que forma uma clique. Uma
é um grafo clique com exactamente
k
k -clique
vértices. O problema clique é determinar se um
grafo contém uma clique de um determinado tamanho.
LCLIQU E = hG, ki|G
é um grafo não direccionado e contém uma
(b) Dado um conjunto de números
existe um subconjunto de
X
X = {x1 , x2 , . . . , xn }
e um valor
tal que a soma dos números é
t
k -clique
queremos saber se
t.
X
LSU BSET −SU M = hX, ti|X = {x1 , x2 , . . . , xn } ∧ {y1 , y2 , . . . , yl } ⊆ X ∧
yi = t
i
Page 5
4. O que caracteriza as linguagens da classe de complexidade temporal
P?
E as da classe
NP?
Considere as frases seguintes; diga, JUSTIFICANDO, se são verdadeiras, falsas, ou se nada
pode concluir acerca da sua veracidade:
(a)
P 6= NP
(b)
P ⊆ NP
(c)
NP ⊆ P
5. Explique de forma clara e concisa o que tem que fazer se quiser provar que uma dada
linguagem L é
NP-completa.
Que outra forma tem de provar que uma linguagem é
NP-
completa?
6. Para além do tempo e do espaço existem outros recursos que são usados para classicar as
linguagens. Um desses recursos é o acesso a números aleatórios. Um
algoritmo probabilístico
utiliza o resultado de um processo aleatório. Que acrescentos são necessários fazer ao modelo
BURM para podermos estudar este tipo de algoritmos e classes de complexidade?
7. No contexto do Teorema de Cook, apresente as fórmulas conjuntivas que descrevem o transição das instruções BURM.
8. Mostre que a linguagem
COBV
é
NP-completa.
Page 6