Metodo de Pontos Interiores Aplicado a um Problema de

Propaganda

Universidade Federal da Bahia
Instituto de Matemática
Curso de Pós-graduação em Matemática
Dissertação de Mestrado
Método de Pontos Interiores Aplicado a um
Problema de Seqüenciamento Job-Shop
Alexander dos Santos Dutra
Salvador-Bahia
Novembro/ 2004
Método de Pontos Interiores Aplicado a um
Problema de Seqüenciamento Job-Shop
Dissertação apresentada ao colegiado do curso de Pós-Graduação em Matemática da
Universidade Federal da Bahia, como requisito parcial para obtenção do Tı́tulo de
Mestre em Matemática Pura.
Banca examinadora
Prof. Dr. Isamara Carvalho Alves (Orientador).
Prof. Dr. Akebo Yamakami
Prof. Dr. Carlos Eduardo Trabuco Dórea
Dutra, A.
“Método de Pontos Interiores Aplicado a um Problema
de Seqüênciamento Job-Shop. ” / Alexander dos Santos Dutra.
Salvador-Ba, 2004.
Orientador: Isamara de Carvalho Alves (Universidade Federal da
Bahia).
Dissertação de Mestrado apresentada ao curso de Pós-graduacão em
Matemática da UFBA, 99 páginas.
Palavras-Chave:Programação Não-Linear, Método de Pontos Interiores, Lagrangeano Aumentado, Problemas de Seqüenciamento Job-Shop.
A Deus, á minha amada e
aos meus pais.
“Não há nada a temer a menos que
me esqueça de como Deus me conduziu até aqui. ”
Ellen White.
Agradecimentos
A Deus, pelos sinais e maravilhas operadas na vida de minha famı́lia durante
este perı́odo de estudos. O Senhor tornou realidade aquilo que todos julgávamos impossı́vel. A Deus todo louvor por mais esta vitória.
A Suzy, Alexander Junio e Adrielle. Suzy, minha esposa amada, sou grato por
acreditar em mim mesmo nos momentos que nem eu pude acreditar, seu amor faz de
mim o que sou. Meus filhos, Alexander Junio e Adrielle, não foi fácil ter papai tanto
tempo perto dos olhos e com a mente tão distante, obrigado por me fazerem sorrir.
A todos os colegas de mestrado agradeço pelo companheirismo e amizade.
Aos grandes matemáticos e amigos Andrade, Augusto, Fábio e Gustavo obrigado pela
contribuição sempre iluminada nos estudos. José Luı́s, obrigado pelo incentivo e apresentação a esta linha de pesquisa que tanto me fascina. Ernesto, meu companheiro de
pesquisa saiba que tem sido ”massa”trabalhar contigo.
Aos professores que contribuı́ram para que este momento fosse possı́vel. Em
particular sou grato aos professores José Fernandes, Elinalva Vergasta e Marco Antônio
pelo incentivo e apoio para que pudesse enfrentar esta etapa de estudos.
Um agradecimento especial a professora Isamara Alves pela orientação e disponibilidade constante.
Resumo
O problema de seqüenciamento do tipo job-shop é um problema que desperta
o interesse de pesquisadores por sua caracterı́stica computacional na categoria de um
problema NP - difı́cil . Além disto, como um problema de programação matemática, o
job-shop constitui um particular desafio por possuir um espaço de busca não convexo.
Tratamos neste trabalho de um problema de job-shop estático, determinı́stico
e com máquinas especializadas, para o qual adotamos uma modelagem matemática
contı́nua e não linear. É verdade que modelos de programação não linear são muitas
vezes evitados em função da dificuldade encontrada em garantir a convergência para
um mı́nimo global. Contudo, essa dificuldade pode ser superada com o uso do Método
de Pontos Interiores (MPI) o qual tem sido aplicado com sucesso na resolução de
problemas dessa natureza. Este trabalho realiza, portanto, uma análise matemática a
fim de viabilizar o uso de MPI na resolução de um problema de job-shop especı́fico.
Propomos o uso de MPI associado com o Lagrangeano Aumentado que foi
usado para guiar o algoritmo por um caminho decrescente para a função objetivo.
Para tal, foi preciso alterar algumas das informações de segunda ordem a fim de encontrar direções primais que garantam esse decrescimento. Mostramos que as mudanças
efetuadas não alteram a convergência do problema primal, porém a convergência do
problema dual é influenciada. Em função disso, adotamos uma variação na direção
dual ajustando-a à função de penalidade usada e determinamos as condições favoráveis
à convergência para um ponto que minimize a função objetivo do problema tratado.
Palavras Chave: Programação Não-Linear, Método de Pontos Interiores,
Lagrangeano Aumentado, Problemas de Seqüenciamento Job-Shop.
Abstract
The job-shop-type scheduling problem is an issue that has called the attention
of researchers because of its computational characteristic in the category of an NPhard problem. Besides, as a mathematical programming problem, job-shop poses a
particular challenge because it comprises a non-convex search environment.
We deal, here, with a specific job-shop problem for which we adopt a continuous, non-linear mathematical model. Non-linear programming models are often
avoided viz-à-viz the difficulty we meet when we try to ensure the convergence to a
global minimum. However, this difficulty can be overcome with the use of the Interior
Point Method (IPM), which has been successfully applied when we try to solve problems of this kind . This thesis proposes, therefore, a mathematical analysis in order to
make possible the use of IPM in the resolution of a specific type of job-shop problem.
We propose the use of IPM together with a Augmented Lagrangean so as
to lead the algorithm in a decreasing way towards the objective function. For that
reason, we needed to alter a few items of second-order information so that we could find
primal directions to ensure that reduction. We shall demonstrate that the accomplished
changes did not significantly alter the convergence of the primal problem. Nevertheless,
the convergence of the dual problem is affected. On account of that, we have resorted
to a variation in the dual direction, fine-tuning it to the penalty utilized. By that
means we are able to determine the conditions that are favorable to a convergence to
a point which minimizes the objective function of the problem we are dealing with.
KEY-WORDS: Non-Linear Program, Interior Point Method, Lagrangean
Augmented, Job-Shop Scheduling Problems.
Sumário
Lista de Figuras
xii
Lista de Tabelas
xiii
Introduçao Geral
1
1 O Problema de Seqüenciamento Job-Shop
3
1.1
Problemas de Fábrica . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4
1.2
O Problema de Seqüenciamento Job-Shop . . . . . . . . . . . . . . . .
5
1.2.1
Modelagem por grafos disjuntivos . . . . . . . . . . . . . . . . .
7
1.2.2
Representação de soluções pelo diagrama de Gantt . . . . . . .
8
Formulação Matemática para o Job-Shop . . . . . . . . . . . . . . . . .
10
1.3.1
Critérios de otimização
. . . . . . . . . . . . . . . . . . . . . .
10
1.3.2
Modelo de programação linear com variáveis binárias . . . . . .
11
1.3.3
Modelo de programação não-linear . . . . . . . . . . . . . . . .
12
Métodos de Resolução para o Job-Shop . . . . . . . . . . . . . . . . . .
13
1.4.1
Métodos exatos . . . . . . . . . . . . . . . . . . . . . . . . . . .
13
1.4.2
Métodos heurı́sticos . . . . . . . . . . . . . . . . . . . . . . . . .
14
1.4.3
Métodos de decomposição . . . . . . . . . . . . . . . . . . . . .
15
Conclusão . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
16
1.3
1.4
2 Método de Pontos Interiores
2.1
18
O Método de Pontos Interiores: Ontem e Hoje . . . . . . . . . . . . . .
19
2.1.1
Breve histórico . . . . . . . . . . . . . . . . . . . . . . . . . . .
19
2.1.2
Aplicações do método de pontos interiores . . . . . . . . . . . .
20
2.1.3
O método de pontos interiores versus método simplex . . . . . .
21
2.1.4
Métodos de decomposição e método de pontos interiores . . . .
22
x
2.2
O Método de Pontos Interiores para Programação Linear . . . . . . . .
23
2.2.1
Método primal-dual . . . . . . . . . . . . . . . . . . . . . . . . .
25
2.2.2
O passo central . . . . . . . . . . . . . . . . . . . . . . . . . . .
26
2.2.3
Métodos primais . . . . . . . . . . . . . . . . . . . . . . . . . .
29
Método de Pontos Interiores Aplicado a Programação Não Linear . . .
30
2.3.1
Um método primal-dual barreira-logarı́tmica (PDBL) . . . . . .
31
2.3.1.1
Função de mérito . . . . . . . . . . . . . . . . . . . . .
33
2.3.1.2
Aplicando o Método de Newton . . . . . . . . . . . . .
34
2.3.1.3
Seleção do parâmetros β e µ . . . . . . . . . . . . . . .
36
Um método primal-dual (PD) . . . . . . . . . . . . . . . . . . .
39
Conclusão . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
42
2.3
2.3.2
3 Método de Pontos Interiores Aplicado ao Problema Job-Shop
3.1
3.2
44
Análise do Modelo de Seqüenciamento Job-Shop Adotado . . . . . . . .
45
3.1.1
Análise do Espaço de Busca . . . . . . . . . . . . . . . . . . . .
46
3.1.2
Análise da Hessiana do Lagrangeano . . . . . . . . . . . . . . .
49
Método de Pontos Interiores e o Seqüenciamento Job-Shop . . . . . . .
53
3.2.1
Definições iniciais e funções de mérito . . . . . . . . . . . . . .
54
3.2.2
Mudança da matriz normal N (t, s, y) . . . . . . . . . . . . . . .
56
3.2.3
Um algoritmo de pontos interiores aplicado ao seqüenciamento
job-shop . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
62
3.2.3.1
Ponto de partida e parâmetros iniciais . . . . . . . . .
63
3.2.3.2
Encontrando as direções de busca . . . . . . . . . . . .
66
3.2.3.3
Definindo o tamanho de passo . . . . . . . . . . . . . .
66
Análise de Convergência . . . . . . . . . . . . . . . . . . . . . . . . . .
69
3.3.1
Condições para a convergência global do problema de job-shop .
69
3.3.2
Prova de Convergência . . . . . . . . . . . . . . . . . . . . . . .
70
Conclusão . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
81
3.3
Conclusão Geral
82
Referências Bibliográficas
85
A Tópicos de Programação Não-Linear
91
xi
A.1 Tipos de Funções . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
91
A.2 Condições de Otimalidade para Problemas com Restrições . . . . . . .
92
A.3 Regra de Armijo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
95
A.4 Função de mérito . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
95
B Algoritmos Sugestivos
97
B.1 Algoritmo para ajuste da matriz Normal Nβ . . . . . . . . . . . . . . .
97
B.2 Algoritmo sugestivo de MPI . . . . . . . . . . . . . . . . . . . . . . . .
98
Lista de Figuras
1.1
Grafo potencial-tarefa representando problema-exemplo 1 de job-shop. .
1.2
A representação de uma seleção completa acı́clica para o problema-exemplo
de job-shop. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.3
3.2
9
A representação de duas soluções para o problema exemplo 1 no diagrama de Gantt . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.1
8
9
Gráfico que representa a região de busca referente a uma restrição disjuntiva . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
47
Gráfico da função que representa uma restrição disjuntiva
47
. . . . . . .
Lista de Tabelas
1.1
Dados do problema-exemplo 1 de job-shop. . . . . . . . . . . . . . . . .
7
3.1
Dados do problema-exemplo 2 de job-shop. . . . . . . . . . . . . . . . .
48
3.2
Dados do problema-exemplo 3 de job-shop. . . . . . . . . . . . . . . . .
50
3.3
Dados do problema-exemplo 2 de job-shop. . . . . . . . . . . . . . . . .
63
3.4
Análise ponto inicial . . . . . . . . . . . . . . . . . . . . . . . . . . . .
64
3.5
Análise dos parâmetros para definição das variáveis de excesso e variáveis
3.6
duais . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
65
Exemplo de Aplicação do MPI ao problema de Job-Shop
68
. . . . . . . .
Introdução Geral
O mercado atual possui uma tendência a consumir uma variedade grande de
produtos, com uma vida útil reduzida e com custo o mais baixo possı́vel Jain e Meeran
[29]. Atender a estas necessidades requer processos mais complexos. É preciso buscar
maneiras de economizar em cada detalhe com a finalidade de obter custos competitivos.
Neste contexto, o problema do seqüenciamento de tarefas é freqüente em indústrias e
empresas de um modo geral, que buscam reduzir seu custo operacional e alcançando
uma maior produtividade.
Os problemas de seqüenciamento são essencialmente de otimização restritos
que, num contexto de produção, envolvem descobrir uma seqüência para alocação de
recursos limitados com a finalidade de atender determinado objetivo. Trataremos neste
trabalho de um tipo particular de seqüenciamento em fábrica conhecido por problema
de job-shop.
Apesar da grande relevância prática de problemas de job-shop, há caracterı́sticas teóricas particularmente importantes a serem consideradas. A primeira, diz
respeito a sua complexidade computacional, sendo classificado como um problema NPdifı́cil (Lenstra e Rinnoy Kan [35], Johnson [30]). A segunda, refere-se a seu espaço
de busca de soluções não conexo, despertando assim, o interesse como problema de
programação matemática dada a maior dificuldade na busca de solução por um caminho contı́nuo para este tipo de problema. Estas duas caracterı́sticas agregadas fazem
do problema de job-shop um particular desafio tanto do ponto de vista computacional
como do ponto de vista de análise matemática.
Estamos interessados numa modelagem matemática que possa tratar de forma
Introdução Geral
2
direta a não convexidade do problema em questão. Para tanto, tomamos um problema
de job-shop com caracterı́sticas especı́ficas e adotaremos uma modelagem matemática
contı́nua de programação não linear conforme proposta de E. Pinson [42]. Com esta
modelagem estamos diante de um modelo matemático de programação não linear e não
convexo. Este modelo possui ainda caracterı́sticas particulares que o tornarão ainda
mais desafiador. Diante desses desafios, encontramos no Método de Pontos Interiores
(MPI) um aliado poderoso na busca de solução para o problema de job-shop em questão.
O MPI tem sido utilizado com sucesso na resolução de problemas de programação não linear e não convexos, conforme inúmeras pesquisas encontradas dentre
os quais citamos os trabalhos de El Bakry et al [17], Granville [27] e Vanderbei e
Shanno [56]. Isto nos levou a buscar uma análise mais acurada das caracterı́sticas matemáticas do problema de job-shop buscando garantias de convergência para soluções
que minimizem o tempo de seqüenciamento desejado.
Nosso trabalho está organizado da seguinte forma:
No primeiro capı́tulo apresentamos uma visão geral do problema de job-shop
descrevendo suas principais caracterı́sticas e ressaltando aquelas adotadas em nossa
análise. Também, descrevemos duas formas particulares de modelagem matemática,
além de discutir métodos usados na resolução desse problema.
O MPI é o objeto de nossa atenção no segundo capı́tulo. Partimos de uma
breve visão histórica e seguimos apresentando algumas dentre as inúmeras possibilidades de aplicação deste método que tanto tem despertado o interesse de pesquisadores.
Concluı́mos esta exposição apresentando o método de pontos interiores aplicável a
modelos de programação linear e não-linear.
Os capı́tulos anteriores fornecem subsı́dios para as análises realizadas no terceiro capı́tulo onde verificamos com detalhes o modelo matemático adotado para o
job-shop em questão. Finalizamos este capı́tulo com uma análise de convergência para
o método proposto para a resolução do problema de job-shop.
Capı́tulo 1
O Problema de Seqüenciamento
Job-Shop
O problema de seqüenciamento do tipo job-shop é o mais geral dos problemas de seqüenciamento clássico conforme Jain e Meeran [29]. Este possui um espaço
de busca irregular e caracterı́sticas computacionais capazes de fornecer idéias e informações na busca de algoritmos referentes a outras aplicações práticas. Além disto,
o job-shop é um problema combinatório de complexidade computacional classificado
como NP-difı́cil (Johnson [30], Zwaneveld et al. [59], Strusevich [52]) e sendo considerado um dos mais complexos membros desta classe (Yamada e Nakano [58]).
Uma indicação da complexidade envolvida na busca de solução de um problema
de job-shop pode dado por um problema proposto em 1963 por Muth e Thompson
[40] que consiste no planejamento de 10 tarefas em 10 máquinas, cuja solução ótima
foi provada somente em 1987, por Carlier e Pinson [12].
O objetivo num problema de seqüenciamento job-shop é a realização de determinadas tarefas que podem ser interligadas por restrições de sucessão ou restrições
de localização no tempo. Para execução destas tarefas são necessários certos recursos
(máquinas, mão de obra), os quais introduzem restrições disjuntivas no problema. Os
recursos disjuntivos acrescentam restrições não lineares, formando um espaço de busca
não-convexo.
Problemas de Fábrica
4
Apresentamos, neste capı́tulo, as caracterı́sticas básicas referente ao seqüenciamento job-shop já restrito às caracterı́sticas a que nos propomos estudar. Analisamos,
em seguida, alguns modelos matemáticos e métodos de resolução comumente usados.
1.1
Problemas de Fábrica
Problemas de fábrica são problemas onde se pretende seqüenciar a execução
das operações necessárias à confecção de determinados produtos que passam por máquinas distintas ou não (Alves [3]) com o objetivo de minimizar o tempo de produção.
Neste caso, as máquinas constituem os recursos a serem compartilhados e os serviços
(jobs) são as operações realizadas na produção de cada item.
Uma máquina pode realizar apenas uma operação de cada vez. Desta forma,
a execução de operações nas máquinas devem ser planejadas a fim de evitar a sobreposição numa mesma máquina num dado instante. O seqüenciamento dos problemas
de fábrica resulta geralmente na procura de seqüências de operações sobre as máquinas.
Podemos considerar problemas de fábrica em que as operações podem ser
realizadas em qualquer máquina (fábrica com máquinas paralelas), casos onde todas
as operações são realizadas numa única máquina, ou ainda, os casos em que uma
operação só pode ser realizada numa determinada máquina (fábrica com máquinas
especializadas). Dentre os problemas de fábrica com máquinas especializadas podemos
distinguir os seguintes casos principais:
• problema de open-shop - quando as operações elementares são independentes, ou
seja, a ordem de execução das operações de um mesmo trabalho é indiferente.
• problema de flow-shop - quando as operações elementares dos trabalhos são ligadas por uma mesma ordem total, ou seja, todos os produtos seguem um percurso
unidirecional.
• problema de job-shop - quando as operações de um trabalho são ligadas por uma
ordem total, não necessariamente idêntica para todos os trabalhos.
O Problema de Seqüenciamento Job-Shop
5
Na prática pode ser que nem todos os produtos estejam disponı́veis para serem
processados no instante inicial. Neste caso, os produtos possuem tempos de partida que
definem a sua data de chegada ao chão da fábrica. Os tempos de partida dos produtos
são eventos que não podem ser previstos, portanto seus requisitos de processamento
também não podem ser conhecidos com antecedência. Neste caso o seqüenciamento de
tarefas torna-se um problema não determinı́stico que deve ser realizado em um perı́odo
de tempo totalmente aberto, sendo definido como um problema dinâmico.
Podemos considerar também o caso em que, uma vez iniciado o processo de
produção, os recursos utilizados por cada atividade não podem mais ser alterados até
que todos os produtos estejam concluı́dos. Nesse sistema ideal, todos os recursos estão
sempre disponı́veis no inı́cio do perı́odo de seqüenciamento, e não existe a possibilidade de interrupção do processo ora iniciado. Problemas com estas caracterı́sticas são
conhecidos como problemas estáticos, e, apesar de serem pouco prováveis em situações
reais, o seu estudo é de fundamental importância para o desenvolvimento de técnicas
eficazes para a solução de problemas dinâmicos.
1.2
O Problema de Seqüenciamento Job-Shop
Neste trabalho trataremos o problema de job-shop de um ponto de vista
industrial. Teremos como recurso básico a utilização de máquinas capazes de executar
apenas uma tarefa de cada vez, sendo por este motivo, consideradas como recursos
disjuntivos. Geralmente, chama-se a confecção de certo produto, de trabalho (job). As
operações de um mesmo trabalho são organizadas em seqüências conhecidas por gama
operatória.
Podemos classificar o problema a que nos propomos lidar como um problema
de job-shop estático e determinı́stico com máquinas especializadas, pois estaremos supondo que todos as informações sejam conhecidas antecipadamente (estático) e os dados
perfeitamente determinados (determinı́stico). As máquinas são consideradas especializadas pois cada produto possui uma lista de operações com uma seqüência pré-definida.
Estaremos admitindo que as máquinas são independentes umas das outras,
O Problema de Seqüenciamento Job-Shop
6
estando disponı́veis todo o perı́odo de atividade, mas não podendo executar mais de
uma tarefa ao mesmo tempo. Consideraremos também que não existe prioridade na
execução de determinada tarefa; assim não será possı́vel interromper a execução de
uma operação para realização de outra.
Quanto aos produtos, consideraremos produtos independentes sem prioridades
na execução de suas operações. Cada produto deverá ser processado em dada máquina
uma única vez e eles deverão respeitar uma ordem de execução dentro da gama operatória. Além disto, consideraremos que os produtos chegam na unidade produtiva
num mesmo instante.
Estudaremos casos de unidades fabris contendo m
e máquinas distintas e p produtos. Cada produto Pi é constituı́do de pi operações elementares. Desta forma, numa
p
X
fábrica serão executadas p0 =
pi operações, cada uma delas sendo realizada em
uma máquina diferente Mk .
i=1
O número total de operações que é executada em uma máquina Mk será denotado por m
e k . A duração de execução de uma operação Oj em Mk será chamada de
tempo operatório e denotada por dj . Durante este tempo, a máquina estará ocupada e
todas as outras operações nesta máquina terão que aguardar para serem processadas.
Assim, toda operação em uma máquina terá seu tempo de inı́cio de processamento
denotado por tj que depende do instante de finalização da operação precedente nesta
máquina. O instante de término de execução de uma operação Oj será denotado por
Cj , sendo Cj = tj + dj .
Os problemas de seqüenciamento job-shop, que denotaremos por Πj são constituı́dos por:
• P = {Pi |i = 1, ..., p} - o conjunto de p produtos (ou trabalhos) Pi .
• M = {Mk |k = 1, ..., m}
e - o conjunto de m
e máquinas Mk .
• O = {Oj |j = 1, ..., p0 } - o conjunto de todas as operações Oj .
Para tornar mais claras as definições aqui vistas, apresentaremos um exemplo
de um problema de job-shop (problema-exemplo 1) onde os dados estão na tabela 1.1.
O Problema de Seqüenciamento Job-Shop
p=4
e
p1 = p2 = p3 = 3,
7
m
e =3
p0 = 11
p4 = 2
m
e1 = m
e 2 = 3,
produto
operação
duração
máquina
1
1
3
2
1
2
3
3
1
3
1
1
2
4
3
3
2
5
2
2
2
6
3
1
3
7
1
2
3
8
4
1
3
9
4
3
4
10
4
1
4
11
3
2
m
e3 = 2
Tabela 1.1: Dados do problema-exemplo 1 de job-shop.
1.2.1
Modelagem por grafos disjuntivos
Os problemas de job-shop também podem ser descritos através de uma mode-
lagem por grafos conforme proposto por Balas et al. [1]. Consideremos então o grafo
disjuntivo G = (V, C ∪ D), onde:
• V é um conjunto de nós que representam as operações Oj de cada produto unido
a duas operações fictı́cias , fonte (O0 ) e sorvedouro (Of im ).
• C é o conjunto de arcos conjuntivos que representa a seqüência tecnológica das
operações dentro de um mesmo produto, ou seja, a ordem em que as operações
Oj de um mesmo produto pi devem ser processadas. Cada arco é ponderado de
acordo com o tempo de execução da operação que o origina (Oj ).
• D é o conjunto dos arcos disjuntivos que representam as restrições de capacidade
das máquinas, cada arco é ponderado com o tempo de execução de sua operção
respectiva, existem portanto pares de arcos ((Ou → Ov ), (Ov → Ou )) que devem
ser realizadas na mesma máquina Mk .
Desta forma os problemas de seqüenciamento job-shop podem ser vistos como
de definição da ordem entre todas as operações que devem ser processadas na mesma
O Problema de Seqüenciamento Job-Shop
8
máquina, isto é, determinar a precedência entre estas operações. No modelo de grafo
disjuntivo isto é realizado definindo direções para todos os arcos disjuntivos. Assim,
temos que uma seleção é um conjunto de arcos direcionados selecionados de arcos
disjuntivos. Por definição, uma seleção é completa se todas as disjunções forem selecionadas e esta seleção será consistente se o grafo direcionado resultante for acı́clico.
3
3
1
O1
O2
O3
3
2
3
O4
O5
O6
0
O0
0
1
4
4
O7
O8
O9
3
4
2
O11
O10
MAQUINA
1
´
MAQUINA
´
2
Ofin
O12
MAQUINA
´
3
Figura 1.1: Grafo potencial-tarefa representando problema-exemplo 1 de job-shop.
Na figura 1.1 apresentamos o grafo para o problema-exemplo 1. Nele é possı́vel
ver o conjunto de arcos conjuntivos C representados pelas flechas contı́nuas e o conjunto
de arcos disjuntivos D representados pelas flechas pontilhadas. Cada operação é representada por um nó e os arcos que partem de cada nó são ponderados pelo duração da
operação correspondente. Neste exemplo todos os produtos são lançados no instante
0. Uma seleção completa com a definição de todas as direções no arcos disjuntivos é
representada pela figura 1.2
1.2.2
Representação de soluções pelo diagrama de Gantt
Uma forma útil para visualizar uma solução encontrada para um problema de
seqüenciamento job-shop é o diagrama de Gantt. Este diagrama representa a ocupação
das máquinas em função do tempo. A construção deste diagrama é feita associando
a cada máquina Mk uma barra horizontal onde as operações são representadas por
O Problema de Seqüenciamento Job-Shop
9
3
3
1
O1
O2
O3
3
2
3
O4
O5
O6
0
0
O0
1
4
4
O7
O8
O9
3
4
2
O11
O10
MAQUINA
´
2
´
MAQUINA
1
Ofin
O12
MAQUINA
´
3
Figura 1.2: A representação de uma seleção completa acı́clica para o problema-exemplo de job-shop.
retângulos localizados nesta barra. Os retângulos possuem o comprimento proporcional
à duração da operação que representa e a posição que ocupa na barra é definida pelo
instante de inı́cio da respectiva operação. A figura 1.3 apresenta o diagrama de Gantt
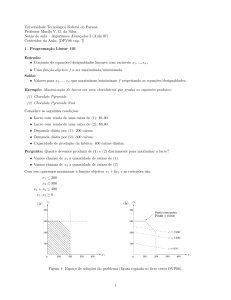
para o problema-exemplo 1 de job-shop onde é possı́vel constatar a superioridade da
segunda solução (S2 ) com tempo total de produção igual a 13 unidades de tempo em
relação à primeira (S1 ) com tempo total de produção igual a 33 unidades de tempo.
M1
P1
P2
M2
P3
M3
P4
0
~ S :
Solucao
1
´
C
= 33
max1
33
tempo
M1
P1
P2
M2
P3
P4
M3
0
13
~ S :
Solucao
2
´
tempo
C
= 13
max2
Figura 1.3: A representação de duas soluções para o problema exemplo 1 no diagrama de Gantt
Formulação Matemática para o Job-Shop
1.3
10
Formulação Matemática para o Job-Shop
As restrições disjuntivas introduzem um espaço de busca não convexo para
seqüenciamento job-shop. A linearização destas restrições pode ser feita acrescentandose variáveis binárias na formulação do problema, obtendo-se um modelo inteiro-misto.
O mesmo problema também pode ser modelado de forma contı́nua como um problema
de programação não linear. Apresentaremos a descrição de uma proposta de formulação
matemática de cada tipo além de critérios de otimização que podem ser considerados.
1.3.1
Critérios de otimização
O objetivo a ser alcançado num problema de seqüenciamento job-shop aplicado
ao chão de fábrica é otimizar o tempo total de produção. Há vários critérios que podem
ser utilizados na otimização de tais problemas (Ramos [44]). Um critério de otimização
comumente usado é a minimização da duração total do seqüenciamento denominado
makespan e denotado por Cmax , sendo:
Cmax = max {Ci }
1≤j≤p
onde Ci é o momento de término de execução de um produto Pi , ou seja, Ci é momento
do término de execução da última operação referente a esse produto.
Uma outra forma igualmente útil de avaliar o tempo de produção total é pela
soma de todos os tempos de inı́cio de todas as n0 operações tj . Esta forma apresenta
como critério de otimização uma função linear definida por:
f (t) =
p0
X
tj
(1.1)
j=1
Existe ainda uma diversidade grande de critérios empregados na otimização
de um problema de job-shop. Uma descrição destes critérios pode ser encontrada
no trabalho de Ramos [44]. Neste trabalho estaremos utilizando como critério de
otimização a soma dos tempos de inı́cio das operações conforme função (1.1) pela
facilidade que ela oferece à análise geral do problema de job-shop.
Formulação Matemática para o Job-Shop
1.3.2
11
Modelo de programação linear com variáveis binárias
Uma forma comumente encontrada para tratar as restrições disjuntivas é o uso
de variáveis binárias. Uma das propostas de modelagem desta natureza é a feita por
Manne e citado por Thompson, et al [55] que define uma nova variável binária para
cada par ordenado de operações utilizando a mesma máquina. Esta variável em 0-1 é
denotada por yuv , tal que:
yuv

 1,
=
 0,
se Ov precede Ou sobre Mk
se Ou precede Ov sobre Mk .
Este modelo também utiliza um limite superior B para duração total do
seqüenciamento. Este limite pode ser, por exemplo, a soma de todos os tempos operatórios das operações do problema:
B=
p0
X
dj .
(1.2)
j=1;
As restrições do problema podem ser expressas pelas equações:
h
tj+1 ≥ tj + dj ,
(1.3)
∀j ∈ C
h
h
∀(u, v) ∈ D
(1.4)
tu ≥ tv + dv − B(1 − yuv ), ∀(v, u) ∈ D
(1.5)
tv ≥ tu + du − B(yuv ),
As restrições (1.3) representam as restrições da gama operatória. As restrições
(1.4) e (1.5) representam as restrições disjuntivas. Neste modelo, para cada escolha de
um par de arcos disjuntivos, somente uma das restrições (1.4) e (1.5) é ativada. Assim,
quando se escolher fazer Ou antes de Ov (yuv vale 0) a restrição (1.5) é então inativa
p0
X
já que tu ≥ tv + dv − B, e da forma em que B foi definida (como
dj ) o segundo
j=1
termo desta inequação será sempre negativo e, como consideramos todos os tempos de
inı́cio sendo positivos, esta restrição fica inutilizada. Por outro lado, a restrição (1.4) é
ativada já que torna-se
tv ≥ tu + du .
(1.6)
Formulação Matemática para o Job-Shop
12
Neste caso o makespan pode facilmente ser obtido acrescentando-se uma nova
variável (tf im ) para representar o momento de término de toda a produção e o seguinte
conjunto de restrições:
h
tf im ≥ tj + dj ,
∀j ∈ O
Dessa forma um problema de seqüenciamento job-shop Πj pode ser escrito como:
M in.
f (t) = tf im
S.a.
tj + dj − tj+1 ≤ 0 ∀(j, j + 1) ∈ C
tu + du − B(yuv ) ≤ tv ∀(u, v) ∈ D
tv + dv − B(1 − yuv ) ≤ tu ∀(v, u) ∈ D
tj + dj ≤ tf im ∀j ∈ O
tj ≥ 0 ∀j ∈ O
Obtemos assim um problema de programação inteira-mista. A principal dificuldade na resolução desse modelo refere-se às variáveis inteiras (binárias). Uma forma
comum na resolução desse modelo consiste na junção de um método de Branch-andBound com o método simplex.
1.3.3
Modelo de programação não-linear
O modelo proposto por Pinson [42] agrupa em uma única equação quadrática
as duas equações disjuntivas para cada par de operação numa mesma máquina Mk . As
restrições deste modelo são representadas pelas equações:
tj + dj
≤ tj+1 ,
∀j ∈ C
(tv − tu + dv )(tu − tv + du ) ≤ 0, ∀(u, v) ∈ D
(1.7)
(1.8)
As restrições (1.7) representam as restrições da gama operatória. As restrições
(1.8) representam as restrições disjuntivas das máquinas. Essas restrições disjuntivas
introduzem um espaço de busca contı́nuo mas não conexo.
Acrescentando a este conjunto de restrições o critério de otimalidade expresso
pela função (1.1) obtemos o seguinte problema de programação não-linear para um
problema de seqüenciamento job-shop
Métodos de Resolução para o Job-Shop
M in.
13
n0
X
f (t) =
tj
j=1
S.a.
tj + dj − tj+1 ≤ 0 ∀j ∈ C
(1.9)
(tv − tu + dv )(tu − tv + du ) ≤ 0 ∀(u, v) ∈ D
tj ≥ 0 ∀j ∈ O
Modelos de programação não linear e não convexo têm sido evitados em função
das dificuldades encontradas na busca de solução por métodos tradicionais [57]. O
método de pontos interiores é uma ferramenta capaz de superar este problema conforme
apresentado na seção 2.3.
1.4
Métodos de Resolução para o Job-Shop
A solução de um problema de seqüenciamento job-shop pode ser obtida por
métodos exatos, mas devido a sua complexidade (NP-difı́cil) em muitos casos só é
viável o uso de métodos que buscam soluções aproximadas para a obtenção de boas
soluções em tempo útil para fundamentar as decisões a tomar no dia-a-dia na indústria.
Métodos de decomposição são também aplicáveis a problemas de job-shop na medida
em que reduzem a dimensão do problema a ser resolvido.
1.4.1
Métodos exatos
Métodos de solução exatos são aqueles que pretendem obter a solução ótima
para um problema no menor tempo possı́vel.
Entre os métodos de solução exata aplicáveis a problemas de otimização combinatória o mais usado é o método de partição e avaliação sucessivas (Branch and
Bound). Encontramos diversos trabalhos nesta direção dentre os quais podemos destacar os trabalhos de Carlier e Pinson ([12], [13]).
As técnicas de programação matemáticas também são métodos exatos, mas
que possuem como desvantagem principal o alto custo computational inviabilizando o
Métodos de Resolução para o Job-Shop
14
seu uso sistemático em casos como o do seqüenciamento job-shop devido a sua complexidade (Np-Difı́cil). Nesta direção, temos os trabalhos de Schall et al ([51], [48], [49],
[50]) que utilizam técnicas de programação matemática de forma hı́brida com métodos
heurı́sticos aplicáveis ao seqüenciamento job-shop modelado de forma linear com o
uso de variáveis binárias. Particularmente, usa técnicas de programação matemática
tendo o método de pontos interiores (MPI) como principal ferramenta de resolução.
As heurı́sticas utilizadas de forma hı́brida com o (MPI) nestes trabalhos são: simulated
annealing e algoritmos genéticos. Tais algoritmos são descritos brevemente na seção
seguinte.
1.4.2
Métodos heurı́sticos
Os métodos de solução aproximada (heurı́sticas) permitem obter planos opera-
cionais aceitáveis em tempo útil, mas não garantem a obtenção de uma solução ótima.
Dentre os diversos métodos aplicáveis ao job-shop, os mais utilizados são os
métodos de lista devido a sua simplicidade. Estes métodos são baseados em regras de
despacho prioritário ou algoritmos de lista (Blazewicz et al.[10], Blazewicz [11]) onde o
plano operacional é construı́do através de uma seqüência de decisões baseadas no que
localmente parece ser ótimo. Alguns algoritmos conhecidos são:
• SPT(Shortest Processing Time) - Seleciona a operação com menor tempo de
processamento.
• EDD (Earliest Due-Date) - Seleciona a operação que pertence à tarefa cuja data
de entrega é a mais próxima.
• FIFO (First In First Out) - Seleciona a operação na ordem crescente de chegada
nas máquinas.
• MWKR (Most WorK Remaining) - Seleciona a operação que pertence ao produto
que tem o tempo de processamento restante maior.
• MOPNR (Most Operations Remaining) - Seleciona a operação que pertence ao
produto que possui o maior número de operações ainda por processar.
Métodos de Resolução para o Job-Shop
15
O método heurı́stico conhecido por Simulated Annealing faz uma analogia
entre a otimização combinatória e a evolução do equilı́brio térmico dos sólidos. No
caso particular do job-shop, busca-se um procedimento iterativo, onde a solução do
problema desempenha o papel do estado energético do sólido. Como mencionado na
seção anterior Schall et al ([50], [51]) propõem uma hibridação do simulated annealing
juntamente com método de pontos interiores para a resolução de problemas de job-shop.
Um outro método heurı́stico utilizado é denominado como Shifting Bottleneck
e foi desenvolvido por Adams et al [1] e consiste em um método iterativo baseado no
grafo disjuntivo. Em cada iteração é resolvido um problema relaxado de planejamento
em uma única máquina com datas de disponibilidade e de entrega, de modo a seqüenciar
as máquinas que formam o problema de job-shop. Assim as máquinas são seqüenciadas
uma de cada vez, seqüencialmente.
Além destes métodos aqui mencionados, vale ressaltar trabalhos realizados com
métodos de busca adaptativos como os algoritmos genéticos (AG) . Estes algoritmos
têm sido aplicados com sucesso a problemas combinatórios. Seu modelo é constituı́do
por uma população de indivı́duos que são soluções potenciais. Os AG combinam o
intercâmbio de informações e a sobrevivência dos melhores indivı́duos, representados
por cadeias estruturadas. Dentre os diversos trabalhos nesta área podemos citar os
trabalhos de Goldberg [25], Yamada e Nakano [58] que são aplicados a problemas de
seqüenciamento job-shop.
1.4.3
Métodos de decomposição
O princı́pio geral destes métodos é o de substituir a resolução de um problema
inicial complexo pela resolução de vários subproblemas cuja resolução seja mais fácil.
A conseqüente redução da dimensão é particularmente importante quando o problema
tem uma complexidade elevada como o caso do job-shop.
Dentre os métodos de decomposição aplicados ao job-shop temos os trabalhos
de Fischer ([19], [20]) que utiliza os multiplicadores de Lagrange para formar o dual
das restrições de máquina. Neste caso, os subproblemas eram constituı́dos pelas res-
Conclusão
16
trições de produto (precedência), e o problema mestre fica encarregado das restrições
de máquina obtendo os multiplicadores de Lagrange de modo a manter a factibilidade.
Num outro trabalho, Fischer [21] propõe uma metodologia que realiza um procedimento
próximo da Relaxação Lagrangeana clássica.
Métodos de decomposição espacial são aplicados a problemas de job-shop de
grande dimensão reagrupando máquinas em células de produção e os produtos em
famı́lias de forma que produtos de uma mesma famı́lia sejam executados por máquinas
de uma célula principal e, excepcionalmente, sejam executados em máquinas de outras
células. Estas operações que são executadas em outras células são conhecidas como
elementos residuais. Esta filosofia é conhecida como tecnologia de grupos (Kusiak
[33]).
Recentemente temos a proposta de Alves [3] que utiliza a tecnologia de grupos
para particionar o problema de job-shop e, em seguida, utiliza a técnica da relaxação lagrangeana para resolver os subproblemas coordenados por um problema mestre. Neste
caso os subproblemas se aproximam do problema original já que as restrições a serem relaxadas são apenas as referentes ao elementos residuais. Assim, a factibilidade
das soluções locais é garantida de forma mais eficiente. Com o objetivo de tornar
a convergência nesta metodologia mais rápida, Ramos [44] propõe ajustes de alguns
parâmetros no método do subgradiente quando utilizado para resolver o problema mestre.
Ainda há que ressaltar o trabalho de Santana [46] que propõe a decomposição
de um problema de job-shop usando o método de Dantzig-Wolfe.
Conclusão
Neste capı́tulo apresentamos um importante problema de fábrica conhecido
como problema de seqüenciamento job-shop. Verificamos algumas caracterı́sticas especı́ficas do problema de job-shop a que nos propomos a trabalhar (§1.2), seguido de
breve análise de duas particulares formulações matemáticas (§1.3).
Conclusão
17
Neste trabalho estaremos adotando um modelo contı́nuo (§1.3.3) devido à boa
performance apresentada pelo método de pontos interiores na resolução de problemas
de programação não linear, como é o caso. Vamos nos deter agora a uma análise deste
método e suas principais aplicações. A seguir, no capı́tulo 3, veremos que o problema
de job-shop, se constitui num interessante desafio para análise matemática.
Capı́tulo 2
Método de Pontos Interiores
O método de pontos interiores (MPI) tem sido em programação matemática
uma das mais interessantes áreas de pesquisa em otimização desde o desenvolvimento
do método simplex conforme Freund e Mizuno[22]. Diversas formulações de MPI foram
propostas inicialmente tendo em mente problemas de programação linear (Karmarkar
[31], Mehrotra [38], Renegar [45], Wright [57]). Motivados pelo sucesso do MPI para
programação linear tiveram inı́cio as investigações de possı́veis extensões para problemas de programação não linear (Akrotirianakis e Rustem [4],El Bakry, et al. [17],
Granville [27], Vanderbei e Shanno [56]).
Neste capı́tulo fazemos uma breve descrição da relevância do método de pontos
interiores no âmbito da busca de solução de problemas de otimização. Apresentamos
inicialmente uma breve visão histórica do MPI acompanhado de diversas possibilidades
de aplicação às mais variadas áreas. Seguimos apresentando uma descrição sucinta do
MPI aplicado a problemas de programação linear. Finalmente, concluı́mos com a
apresentação de duas versões do MPI aplicado a problemas gerais de programação não
linear.
Método de Pontos Interiores
2.1
2.1.1
19
O Método de Pontos Interiores: Ontem e Hoje
Breve histórico
No ano de 1984 N. Karmarkar [31] apresentou à comunidade cientı́fica um novo
algoritmo para resolver problemas de programação linear em tempo polinomial. Uma
caracterı́stica de tal algoritmo é o fato de chegar a uma solução ótima para o problema
caminhando através de pontos interiores da região viável ao contrário do algoritmo
simplex, que a atinge gerando uma seqüência de pontos extremos adjacentes. O artigo
de Karmarkar [31], e trabalhos anteriores reconhecidos posteriormente, deram inı́cio a
um novo campo chamado de método de pontos interiores.
Nos primeiros anos após o artigo inicial de Karmarkar, os trabalhos em programação linear usando pontos interiores centravam suas atenções em algoritmos que
lidavam com o problema primal, possuindo uma implementação mais amena que o
método original e tendo melhores limites de complexidade. Neste perı́odo é notável a
contribuição do algoritmo de Renegar [45], que usou um limite superior para a função
objetivo obtendo sucessivamente subconjuntos do conjunto factı́vel, cada um contendo
uma solução, e usando o método de Newton para analisar o centro deste subconjunto
primal ótimo. Uma nova era foi inaugurada com o artigo de Megiddo [37], que descreve
uma estrutura para um algoritmo primal-dual. O ponto de vista primal-dual mostrou
ser extremamente produtivo. Isto levou a novos algoritmos com interessantes propostas
teóricas, formando uma base para algoritmos melhores, e extensões para programação
convexa e complementariedade linear. Em 1989, Mehrotra [38] descreve um algoritmo
prático para programação linear que se tornou a base para a maioria dos softwares
existentes; seu trabalho é publicado em 1992.
Os trabalhos em torno do método de pontos interiores tiveram um maior
ı́mpeto após o reconhecimento de soluções de problemas NP-difı́cil obtidas em tempo
polinomial. Os métodos que têm sido propostos possuem vários ingredientes, incluindo
passos do primal-dual, funções com barreira e escalonamento de regiões de confiança.
Método de Pontos Interiores
2.1.2
20
Aplicações do método de pontos interiores
Do ponto de vista teórico várias pesquisas têm sido conduzidas quanto a melho-
ria da eficiência computacional para programação linear (LP), programações quadrática
(QP), problemas de complementaridade lineares (LCP) e algumas classes de problemas
de programações convexos. Outros trabalhos envolvendo método de pontos interiores
(MPI) estão sendo desenvolvidos para programações semi-definidas, os quais possuem
uma grande variedade de aplicações em áreas de controle e otimização estrutural. Programação semi-definida, também tem se mostrado ser uma área de grande impacto
(Potra e Wright [43]).
É possı́vel provar a convergência super-linear de algoritmos primal-dual assumindo a independência linear das restrições ativas nas soluções (Potra e Wright [43]).
Esta observação incitou pesquisas na melhoria das propriedades de convergência de
outros algoritmos, notavelmente programação quadrática. Aplicações à programação
quadrática apresentam-se como uma área promissora devido a habilidade superior que
a aproximação por pontos interiores possui ao explorar a estrutura deste problema.
Como exemplo tem-se, dentre outros, o trabalho de Castro [15] que propõe o MPI
para resolução de problemas de multifluxo de produtos (MFP) com uma formulação
quadrática e verifica um melhor desempenho que o mesmo método aplicado à modelagem linear do mesmo problema.
O MPI tem permitido obter resultados eficientes para problemas de programação não linear, o que tem levado muitos pesquisadores a se dedicarem a esta área
(Akrotirianakis e Rustem [4], El Bakry et al. [17], Granville [27], Vanderbei e Shanno
[56]). Em particular, existe um grande número de trabalhos que aplicam o MPI na
resolução de problemas de fluxo de potência que é um problema de programação não
linear, não convexo e de grande porte. Dentre estes, temos os de Sousa e Costa que,
num primeiro trabalho, apresentam um problema de fluxo de potência ótima resolvido
via MPI primal-dual com barreira logarı́tmica (Sousa e Costa [53]) e, em outro trabalho
(Sousa e Costa [54]), é proposta a determinação das barras para alocações de reativos
a partir de uma análise dos multiplicadores de Lagrange associados às restrições de
igualdade de potência reativa, resultantes de um programa de fluxo de potência ótimo
Método de Pontos Interiores
21
resolvido pelo método apresentado no artigo anterior. Castronuovo et al [16] apresenta
um método baseado na centralização da trajetória da solução ótima onde a distância
entre a solução corrente e o passo central é monitorada.
Problemas de programação inteira também podem ser resolvidos com o auxı́lio
de MPI. Nesta linha temos uma série de trabalhos de Schall et al ([51], [47], [48], [49],
[50]) que estuda a resolução de problemas lineares inteiros fazendo uma hibridização de
métodos exatos (MPI) com outras heurı́sticas tais como: algoritmo genético , simulated
annealing e scatter search. Em particular, em trabalho publicado em 1999 (Schall et
al [51]) é apresentada uma comparação dos métodos discutidos nos artigos anteriores
bem como uma proposta de aplicação a problemas de seqüenciamento job-shop.
Outra aplicação freqüente é o uso de MPI na resolução de problemas de fluxos
em redes de multi-produtos (MFP). Os fluxos em redes de multi-produtos podem ser
usados em diversos campos, como telecomunicações, transportes e logı́stica. Neste
tipo de problema diversos produtos devem ser transportados de um conjunto de nós
de produção para um conjunto de nós de consumo compartilhando a mesma rede de
transporte. Este tipo de problema normalmente tem um grande número de variáveis.
Um trabalho interessante de Azevedo et al [5] propõe a resolução de uma modelagem
por grafos explorando os diferentes graus de esparsidade do problema com o uso de
MPI . Nesta mesma linha há outros trabalhos como o de Castro [14].
O MPI permanece uma área ativa e frutı́fera de pesquisa. Sobretudo, é possı́vel
notar a grande diversidade das aplicações deste método de resolução.
2.1.3
O método de pontos interiores versus método simplex
Diversos autores tentaram comparar implementações de algoritmos de pontos
interiores com o método simplex, mas não obtiveram tempo de solução competitivo.
Com a implementação do método primal apresentado por Karmarkar apresenta-se a
primeira evidência computacional de que MPI pode ser comparado em velocidade com
o método simplex.
A partir daı́, várias implementações de MPI para programação linear foram
Método de Pontos Interiores
22
realizadas com resultado superior ao do método simplex, não necessariamente para
cada problema individual, mas para um conjunto de problemas. De forma prática, para
problemas pequenos o método simplex tem rendimento satisfatório. O MPI justifica-se
particularmente em problemas com grande número de variáveis e maior complexidade
computacional (Wright [57]).
Um exemplo prático onde o MPI possui considerável superioridade sobre o
método simplex é no planejamento do tratamento de câncer por radioterapia onde são
usados modelos de programação linear. Conforme Barbosa [7] neste caso o desafio
matemático consiste em programar a emissão de uma alta dosagem de radiação no
tumor, e simultaneamente, minimizar a radiação nas regiões vizinhas compostas por
tecido saudável. Na presença de múltiplas soluções o MPI convergirá para aquelas
soluções distanciadas dos vértices o que não ocorre com o método simplex. Para este
modelo uma solução próxima do vértice pode não ser a mais adequada do ponto de
vista médico pelo fato das variáveis de folga estarem no seu limite, significando que em
determinadas partes tecido saudável receberá uma dosagem grande de radiação.
Uma vantagem adicional do MPI é a possibilidade de trabalhar com pontos
infactı́veis durante o processo de otimização, facilitando a identificação de modelos mal
formulados (Wright [57]).
2.1.4
Métodos de decomposição e método de pontos interiores
Usar a aproximação por ponto interior nos métodos de decomposição parece
ser promissor, ainda que não estejam sendo feitos estudos comparativos rigorosos nesta
área (Potra e Wright [43]).
Nos métodos de decomposição para problemas lineares e convexos de grande
porte, como a decomposição de Dantzig-Wolfe, método de pontos interiores tem sido
usado para descobrir uma solução para o problema master, ou para obter uma solução
aproximada para os subproblemas gerando pontos de teste. Zhao [60] mostra que
o algoritmo de pontos interiores com a decomposição Dantzing-Wolfe é globalmente
convergente e tem complexidade polinomial. Por sua vez, Gondzio [26] discute os
Método de Pontos Interiores
23
resultados quando o método de pontos interiores é usado como meio de resolução de
um problema master na aproximação por decomposição e aplica sua metodologia a um
problema de multifluxo de produtos de grande porte (5.000 arcos e 10.000 produtos).
2.2
O Método de Pontos Interiores para Programação
Linear
Apesar de boa parte dos modelos matemáticos atuais serem não lineares, for-
mulações de modelos lineares são vantajosas tendo em vista a qualidade dos softwares
à disposição e a garantia da convergência para um mı́nimo global. Portanto, entender o
método de pontos interiores aplicado a problemas de programação linear permite uma
boa visão geral deste método.
Consideremos um problema de programação linear formulado na forma padrão:
Minimizar cT x
Sujeito a
A·x = b
x
(2.1)
≥ 0
onde c e x são vetores do Rn , b é um vetor do Rm e A é uma matriz m×n. Aqui
vale ressaltar que estamos considerando pontos interiores aqueles pontos que atendam
estritamente as restrições do problema (2.1), ou seja, pontos em que x > 0.
Associado com cada problema de programação linear primal existe uma outra
programação linear chamada de dual. O dual para (2.1):
Maximizar bT λ
Sujeito a
At · λ + s = c
s
(2.2)
≥ 0
onde λ é um vetor de Rm e s é um vetor Rn . Nós chamamos as componentes
de λ de variáveis do dual enquanto s é o vetor das variáveis de folga.
O dual e o primal são relacionados por um importante teorema.
Método de Pontos Interiores
24
Teorema 2.1. Considere o vetor x de (2.1) e (λ, s) de (2.2) , então temos que:
bT λ ≤ cT x
Em outras palavras, o valor da função objetivo do dual é limitado inferiormente
pelo valor da função objetivo do primal e o valor da função objetivo do primal é limitado
superiormente pelo valor da função objetivo dual. As duas funções objetivo podem ter
o mesmo valor, de forma que
bλ∗ = cx∗
quando x∗ é solução de (2.1) e (λ∗ , s∗ ) é solução de (2.2).
Teorema 2.2. Pelas condições de otimalidade (kkt) sabe-se que o vetor x∗ ∈ Rn é
solução de (2.1) se e somente se existem vetores s∗ ∈ Rn e λ∗ ∈ Rm que atendem as
seguintes condições
(i)
At λ + s = c
(ii)
Ax
= b
(iii) xi si
= 0 i = 1, 2, ..., n,
(iv) (x, s)
≥ 0
(2.3)
considerando (x, λ, s) = (x∗ , λ∗ , s∗ ).
Os vetores λ e s são geralmente chamados de multiplicadores de Lagrange para
as restrições Ax = b e x ≥ 0, respectivamente. A condição (iii) implica que para cada
ı́ndice i = 1, 2...n uma das componentes xi ou si é nula. Esta condição é conhecida
como condição de complementaridade.
Examinando as condições (2.3) do ponto de vista do primal e do dual, concluı́mos que:
Corolário 2.1. o vetor (x∗ , λ∗ , s∗ ) é solução do sistema (2.3) se e somente se x∗ é
solução de (2.1) e (λ∗ , s∗ ) é solução de (2.2). O vetor (x∗ , λ∗ , s∗ ) é chamado de solução
primal-dual.
Método de Pontos Interiores
2.2.1
25
Método primal-dual
Este método encontra a solução primal-dual (x∗ , λ∗ , s∗ ) aplicando uma variação
do método de Newton nas três equações das condições de (2.3) e modificando a busca de
direções e comprimentos tais que as inequações (x, s) ≥ 0 sejam estritamente satisfeitas
em cada iteração.
Vamos reapresentar as condições de otimalidade (2.3) de uma forma diferente,
considere a função F : R2n+m → R2n+m definida por:

At λ + s − c


F (x, λ, s) =  Ax − b

XSe



=0

(2.4)
(x, s) ≥ 0
X = diag(x1 , x2 , ..., xn )
onde: S = diag(s1 , s2 , ..., sn )
e = (1, 1, ..., 1)t
Note que F é linear nos dois primeiros termos (At λ + s − c, Ax − b) e o único
termo não linear desta função é o termo XSe.
Todos os métodos primal-dual geram em cada iteração pontos (xk , λk , sk ) que
satisfazem estritamente os limites de (2.4), ou seja, xk > 0 e sk > 0. Esta propriedade
é a origem do termo ponto-interior. Respeitando estes limites o método evita soluções
falsas dadas por pontos que satisfazem F (x, λ, s) = 0 mas não (x, s) ≥ 0. Soluções
falsas não fornecem nenhuma informação quanto à solução do primal (2.1) ou do dual
(2.2), por isto é preferı́vel excluı́-las completamente da região de busca. A maior
parte dos métodos de ponto interior requerem que em cada iteração (xk , λk , sk ) seja
estritamente factı́vel, ou seja,(xk , λk , sk ) ∈ F 0 , onde:
F 0 = {(x, λ, s)|Ax = b, At λ + s = c, (x, s) > 0}
Como mencionado, o procedimento para obter uma direção de busca tem sua
Método de Pontos Interiores
26
origem no método de Newton que forma um modelo linear para F em torno do ponto
corrente e obtém a direção de busca (∆x, ∆λ, ∆s) para a solução do seguinte sistema
de equações lineares:


∆x




J(x0 , λ0 , s0 )  ∆λ  = −F (x0 , λ0 , s0 )


∆s
sendo J o Jacobiano de F . Se o ponto corrente é estritamente factı́vel, o passo de
Newton torna-se:


O A


 A 0

S 0
t


0
∆x
 

 

0   ∆λ  =  0
 

−XSe
∆s
X
I





(2.5)
Um passo completo nesta direção é usualmente não permitido, já que poderia
violar o limite de não negatividade (x, s) ≥ 0. Para evitar esta dificuldade, caminha-se
ao longo da direção de Newton (2.5), só que a nova iteração é dada por:
(x, λ, s) + α(∆x, ∆λ, ∆s) onde α ∈ (0, 1]
Infelizmente quando o ponto corrente está próximo ao limites do espaço de
busca só podemos tomar pequenos passos (α << 1) sem violar a condição de (x, s) > 0,
por este motivo o método de Newton oferece pouco progresso na busca da solução. É
necessário, portanto, fazer algumas mudanças no método de Newton original.
2.2.2
O passo central
O passo central C pode ser definido como sendo o arco de pontos (xτ , λτ , sτ ) ∈
F 0 parametrizado por um escalar positivo τ . Cada ponto de C satisfaz as condições
abaixo:
(i)
At λ + s = c
(ii)
Ax
= b
(iii) xi si
= τ i = 1, 2, ..., n,
(iv) (x, s)
> 0
(2.6)
Método de Pontos Interiores
27
Essas condições diferem das condições KKT (2.3) unicamente pelo termo τ na
terceira condição . Esta é a chave para os pontos do arco C, pois cada produto xi si
tem o mesmo valor. O passo central, portanto, equilibra o algoritmo primal-dual por
prover uma rota que pode ser seguida dentro do conjunto solução.
Uma outra forma de definir C é usando a notação de (2.4) e escrever


0




F (xτ , λτ , sτ ) =  0  , (xτ , sτ ) > 0


τe
(2.7)
A equação (2.7) se aproxima de (2.4) quando τ tende a zero. Se C converge
sempre que τ → 0, esta converge para a solução primal-dual da programação linear.
O passo central deste modo guia a solução ao longo de uma rota que evita soluções
indesejadas fixando todo produto xi si estritamente positivo e decrescendo até zero com
alguma taxa.
Boa parte dos algoritmos primal-dual fazem passos de Newton em torno de
pontos de C para τ > 0 ao invés de um passo de Newton puro para F . Para descrever a
inclinação da direção de procura, usa-se um parâmetro central σ ∈ [0, 1] e uma medida
de dualidade µ definidos por:
n
1X
xT s
µ=
xi s i =
n i=1
n
que mensuram um valor médio para o produto xi si . A equação genérica para distância
torna-se:


O A


 A 0

S 0
t


0
∆x
 

 

0   ∆λ  =  0
 

−XSe + σµe
∆s
X
I





(2.8)
A distância (∆x, ∆λ, ∆s) é um passo de Newton para o ponto (xσµ , λσµ , sσµ ) ∈
C, onde todo os produtos (xi si ) são iguais a σµ.
Se σ = 1, a equação (2.8) define uma direção central, ou seja, um passo de
Newton na direção do ponto (xµ , λµ , sµ ) ∈ C, em que todos os pares de produtos xi si
Método de Pontos Interiores
28
são iguais a µ. No outro extremo, o valor de σ = 0 refere-se ao passo de Newton
original (2.5). Muitos algoritmos usam valores intermediários de σ no intervalo (0, 1)
com a dupla finalidade de reduzir µ e melhorar a centralidade.
É possı́vel provar que se F 0 6= ∅ então (2.6) tem solução (xτ , λτ , sτ ) para
cada τ > 0. Mais ainda, as componentes x e s desta solução são únicas. Para tanto,
considere H0 como a projeção de F 0 no espaço reduzido de vetores (x, s), definido por:
H0 = {(x, s)|(x, λ, s) ∈ F 0 para algum λ ∈ <m }
e então identifique (xτ , sτ ) como o menor valor de H0 da função barreira definida por
j=1
fτ (x, s) =
X
1 T
x s−
log(xj sj )
τ
n
as componentes x e s são definidas unicamente se a matriz A tem posto completo. A
função fτ (x, s) aproxima-se do infinito sempre que (x, s) se aproxima da fronteira de
H0 , ou seja, sempre que algum par primal-dual xj sj se aproxima de zero. Acerca de
fτ também pode se afirmar (Wright [57]) que:
• fτ é estritamente convexa em H0
• fτ é limitada por H0
• Dado τ > 0, e algum número K, todos os pontos (x, s) no plano do conjunto
{(x, s) ∈ H0 |fτ (x, s) ≤ K} satisfazem
xi ∈ [Ml , Mu ], si ∈ [Ml , Mu ], i = 1, 2, ..., n
sendo Ml , Mu números positivos.
temos os seguinte teorema apresentado por (Wright [57]):
Teorema 2.3. Suponha que F 0 6= ∅, e tome um número positivo τ . Então fτ tem um
único mı́nimo local em H0 e as condições para o passo central (2.6) têm solução.
O passo central também pode ser definido como uma seqüência de valores
mı́nimos de uma função de barreira logarı́tmica para o dual ou para o primal. Na
próxima seção ver-se-á o caso de uma função de barreira para o problema primal.
Método de Pontos Interiores
2.2.3
29
Métodos primais
Algoritmos primais também têm sido incorporados a algoritmos para pro-
gramação não linear da mesma forma que algoritmos primal-dual.
Um elemento importante na maioria dos algoritmos primais é a aproximação
com o uso da função barreira logarı́tmica para (2.1), que é definida como:
i=1
X
min T
c x−τ
logxi sujeito a Ax = b, x > 0
x
n
(2.9)
onde τ > 0 é um parâmetro positivo. Note que o domı́nio desta função é
o conjunto de pontos estritamente factı́veis para o problema 2.1. Para atender as
condições de otimalidade a solução xτ de (2.9) satisfaz as seguintes condições:
(i)
τ X −1 e + At λ = c
(ii)
Ax
(iv) (x, s)
= b
(2.10)
> 0
para λ ∈ Rm . Podemos definir o vetor s por
si =
τ
, i = 1, 2, ..., n
xi
estas condições são transformadas nas condições do passo central (2.3). Portanto, o valor mı́nimo xτ do subproblema com barreira logarı́tmica (2.10) é simplesmente a componente x do vetor de passo central (xτ , λτ , sτ ) ∈ C.
Quando τ decresce até zero, xτ aproxima-se da solução x∗ do problema de
programação linear (2.1). Soluções do problema (2.9) para cada valor de τ pode ser
formada, por exemplo, pelo uso do método de Newton.
Algoritmos baseados em funções de barreira logarı́tmica não se tornaram populares tanto em programação linear quanto em programação não linear, devido a
dificuldade crescente de tornar o parâmetro de barreira τ tender a zero. O interesse
neste algoritmo foi reavivado em 1985 quando se notou a relação entre o algoritmo de
Karmarkar e algoritmos de barreira logarı́tmica.
Método de Pontos Interiores Aplicado a Programação Não Linear
30
Algoritmos de Karmarkar avaliam o progresso na direção ótima através da
média de uma função potencial logarı́tmica. Uma variante da função deste algoritmo é
T
(n + 1)log(c x − Z) −
n
X
logxi
i=1
onde Z é um limite inferior para o valor objetivo de (2.1), que pode ser obtido
durante as iterações pelo uso de informações do problema dual. Logo após Karmarkar,
Renegar [45] desenvolveu um algoritmo que usa o método de Newton em conjunto com
uma função logarı́tmica, definida por:
T
minx − nlog(Z − c x) −
n
X
xi
i=1
(2.11)
T
sujeito a Ax = b, x > 0, c x < Z
onde Z é um limite superior para o valor ótimo Z ∗ do objetivo cT x para (2.1).
De fato cada solução de (2.11) é um passo primal central. O algoritmo de Renegar
seguiu este passo usando o método de Newton para obter soluções aproximadas de
(2.11) numa seqüência de valores decrescentes de Z. Ele alcançou um melhor limite de
√
complexidade do que o método de Karmarkar [31], requerendo O( nlog1/²) iterações
para identificar o ponto primal factı́vel x tal que cT x esteja a uma distância ² do valor
objetivo ótimo Z ∗ , para dado ² > 0. Não se tem identificado outro método de pontos
interiores com complexidade melhor do que o apresentado por Renegar.
Apesar do algoritmo de Karmarkar ter se tornado sinônimo de método de
pontos interiores a maior parte dos algoritmos práticos levam em conta a estrutura
primal-dual (Wright [57]).
2.3
Método de Pontos Interiores Aplicado a Programação Não Linear
O método de pontos interiores tem sido muito utilizado tanto em programação
linear quanto em programação não linear ( El-Bakry et al [17], Castronuovo et al [16],
Um método primal-dual barreira-logarı́tmica (PDBL)
31
Granville [27], Sousa e Costa [53][54]). Nesta seção apresentamos uma breve descrição
de uma versão do método primal-dual barreira-logarı́tmica proposto por Vanderbei
e Shanno [56] que é uma versão do método de pontos interiores bastante utilizada
em programação não linear. Em seguida veremos uma versão de método de pontos
interiores primal-dual apresentada por Akrotirianakis e Rustem [4] também útil.
2.3.1
Um método primal-dual barreira-logarı́tmica (PDBL)
O método primal-dual barreira-logarı́tmica (PDBL) aqui apresentado tem como
base o trabalho de Vanderbei e Shanno [56], que permite uma boa visão do método
tanto em casos convexos como em casos não convexos.
Suponha o problema geral de programação não linear representado por:
M in. f (t)
S.a.
g(t) ≥ 0
(2.12)
Consideremos t ∈ Rn e as funções f (t) e g(t) sendo duplamente diferenciáveis.
A resolução do problema (2.12) pelo método PDBL requer que as restrições de desigualdade se transformem em restrições de igualdade, o que pode ser feito pela adição
de variáveis de excesso estritamente positivas (s > 0). É incorporada à função objetivo
uma função barreira-logarı́tmica que garante a não negatividade das variáveis de folga.
Assim o problema (2.12) pode ser reescrito assim:
M in. f (t) − µ ln s
S.a.
g(t) − s = 0
(2.13)
Agora temos para µ > 0, a seguinte função objetivo:
fµ (t, s, µ) = f (t) − µ ln s
(2.14)
A função lagrangeana correspondente ao problema (2.13) é:
L(t, s, y; µ) = f (t) − µln s − y T (g(t) − s)
(2.15)
Um método primal-dual barreira-logarı́tmica (PDBL)
32
As condições de otimalidade de primeira ordem (KKT) para a equação (2.15) são:
∇t L(t, s, y) = ∇f (t) − (A(t))T y = 0
(2.16)
∇s L(t, s, y) = −µe + SY e = 0
∇y L(x, s, y) = (g(t) − s) = 0
onde
A(t) =
∂g(t)
∂t
que é a matriz Jacobiana de g(t)
S é uma matriz diagonal contendo as variáveis de folga sr ;
Y é uma matriz contendo na diagonal os elementos yr ;
e = (1, ..., 1);
∇t f (t) = (1, ..., 1).
Observação 2.1. Note que da segunda equação de 2.16 decorre que y ≥ 0, sendo
consistente com fato de y ser o vetor dos multiplicadores de Lagrange associado com
as inequações relativas ao problema original (2.12).
De forma semelhante ao que foi feito para programação linear podemos reescrever as condições de KKT para equação (2.16) como:
F : R2m+n → R2m+n definida por:

∇f (t) − (A(t))T y


F (t, y, s) =  −µe + SY e

(g(t) − s)



=0

(2.17)
(t, s) ≥ 0
O método de Newton (MN) será usado para encontrar as raı́zes para a função
F (t, y, s). Antes de verificar isto, buscaremos encontrar uma função de mérito que seja
compatı́vel com direção de busca encontrada. A função de mérito será definida com a
única finalidade de guiar e medir o progresso do algoritmo. O objetivo é que ela seja
minimizada com a solução do problema original e, dentro de circunstâncias adequadas
ela servirá como uma função de descida para o algoritmo, decrescendo o seu valor a
cada passo.
Um método primal-dual barreira-logarı́tmica (PDBL)
2.3.1.1
33
Função de mérito
Observando as condições necessárias à otimalidade dada pelas equações (2.16),
é natural pensar na utilização da função
ψ(t, s, y) = ||∇f (t) − A(t)T y||2 + ||SY e||2 + ||g(t) − s||2
(2.18)
como uma forma de mensurar quão próximo o ponto (t, s, y) está da solução.
No trabalho de El-Bakry et al [17] eles utilizam esta função ψ juntamente com
o método de pontos interiores aplicado a problemas de programação não linear. Desde
que a matriz Jacobiana do sistema (2.16) seja não-singular, é mostrado em seu trabalho
que para mudanças adequadas de µ existe uma seqüência de tamanhos de passo {αk }
tais que ψ decresce monotonicamene e as iterações convergem para um ponto em que
ψ = 0 . O sucesso, portanto, do algoritmo baseado nesta função de penalidade está
ligado à não singularidade do Jacobiano.
Outra possibilidade para a função de mérito é uma função de penalidade diferenciável para problemas de programação não-linear estudada por Fiacco e McCormick
[18] e também apresentada por Luenberger [34]. A função proposta é definida por:
Ψ(t, β) = f (t) +
β
||g(t) − s||2
2
(2.19)
A desvantagem teórica desta função é a necessidade de se fazer β → ∞ para
assegurar a convergência para pontos factı́veis que garantam um valor mı́nimo para
o problema original. Entretanto, é utilizada com sucesso (Vanderbei e Shanno [56],
Akrotirianakis e Rustem [4]) de forma conjunta com o método de pontos interiores
aplicado a problemas gerais de programação não linear.
Aplicando esta função de mérito ao problema 2.13 obtemos:
Ψβ,µ (t, s) = f (t) − µ ln s +
β
||g(t) − s||2
2
(2.20)
Esta função de mérito será usada na definição do tamanho do passo obtido
pelo método de Newton para garantir que o algoritmo esteja convergindo para um
ponto onde tenhamos o menor valor para a função objetivo.
Um método primal-dual barreira-logarı́tmica (PDBL)
2.3.1.2
34
Aplicando o Método de Newton
Vamos agora, aplicar o método de Newton à equação 2.17, onde obtemos:
 





T
H(t, y)
0
−A(t)
0
Y
S
A(t)
−I
0




onde H(t, y) = ∇2 f (t) −



T
4t
−∇f (t) + A(t) y








 4s  = 

µe − SY e




4y
−g(t) + s
P
r
(2.21)
yr ∇2t gr (t) e representa a matriz Hessiana do
Lagrangeano.
O sistema (2.21) não é simétrico, mas pode ser facilmente simetrizado, bastando para isto multiplicar a primeira equação por (−1) e a segunda equação por
(−S −1 ), assim temos:

−H(t, y)
0



0
−S −1 Y

A(t)
−I
 
T
A(t)
−I
0






4t
σ






 4s  =  γ



4y
ρ





(2.22)
onde:
• σ = ∇f (t) − A(t)T y
• γ = µS −1 e − y
• ρ = −g(t) + s
Conforme Vanderbei e Shanno [56], neste contexto ρ apresenta uma medida
de infactibilidade para o problema primal (2.13). E, por analogia com programação
linear, é possı́vel referir a σ como uma medida de infactibilidade para o problema dual.
Veja que a segunda equação pode facilmente ser usada para eliminar 4s, neste
caso temos:
4s = SY −1 (γ − 4y)
e o sistema (2.22) pode ser reescrito como:



 

σ
4t
−H(t, y) A(t)T

 = 
 

−1
−1
ρ + SY γ
4y
A(t)
SY
(2.23)
(2.24)
Um método primal-dual barreira-logarı́tmica (PDBL)
35
Verificaremos na seqüencia as condições necessárias para a solução do sistema (2.24)
e procuraremos explicitar fórmulas para as direções de busca. Para tal definamos a
seguinte matriz:
N (t, y, s) = H(t, y) + (A(t))T S −1 Y A(t)
(2.25)
Teorema 2.4. Se N é uma matriz não singular, então (2.21) tem solução única e,
particularmente temos:
4t = −N −1 ∇f + µN −1 AT S −1 e + N −1 AT S −1 Y ρ
4s = −AN −1 ∇f + µAN −1 AT S −1 e − (I − AN −1 AT S −1 Y )ρ
(2.26)
4y = Y S −1 (ρ − AN −1 (−σ + AT (Y S −1 ρ + Y )) + γ
A demonstração deste teorema é simples e é apresentada por Vanderbei e
Shanno [56]. Uma vez que a direção de busca tenha sido definida, o algoritmo processa
interativamente determinando novas estimativas para a solução ótima ao calcular:
tk+1 = tk + αpk 4tk
(2.27)
sk+1 = sk + αpk 4sk
y k+1 = y k + αdk 4y k
A definição do tamanho de passo nos trabalhos [53] e [54] é feita tomando:
h
αp = ςmin
h
αd = ςmin
sj
min
,
4sj <0 |4sj |
yj
min
,
4yj <0 |4yj |
i
(2.28)
1.0
i
1.0
(2.29)
onde ς ∈ (0, 1) é uma constante escolhida para garantir que os vetores contendo
as variáveis s e y não assumam valores exatamente iguais a zero. O valor de ς é
determinado empiricamente; Granville [27] sugere o valor de 0,9995.
Em um de seus trabalhos Vanderbei [56] considera αpk = αdk = como um
tamanho de passo único tanto para as variáveis do primal (tk , sk ), como para a variável
do dual (y k ). Além disso, para controlar o tamanho do passo αk , o algoritmo proposto
Um método primal-dual barreira-logarı́tmica (PDBL)
36
em [56] assegura que para um valor fixo de µ, move-se de uma iteração a outra buscando
minimizar a função
Ψβ,µ (t, s) = f (t) − µ ln s +
β
||ρ(t, s)||2
2
Esta função Ψβ,µ foi definida anteriormente pela equação (2.20) e para que
seja minimizada é necessário que se faça uma seleção adequada do parâmetro β. Na
seção seguinte mostraremos uma critério para seleção de β e αk . Também mostraremos
uma forma para seleção de µ a fim de buscar a solução ótima para o problema original
(2.12), através da redução de µ, tal que µ → 0.
2.3.1.3
Seleção do parâmetros β e µ
Um de nossos objetivos básicos é buscar pontos que atendam as condições de
otimalidade apresentadas na equação (2.16), e isto, pelas condições da equação (2.22)
significa que σ → 0, ρ → 0 e sT y → 0. Vamos, portanto, analisar a convergência
deste método verificando o que acontece com σ, ρ, sT y ao longo das iterações. Os dois
teoremas seguintes são propostos por Vanderbei e Shanno [56].
Teorema 2.5. Denotemos (t, y, s) = (tk , y k , sk ) como sendo o valor das variáveis na
iteração k e por (t, y, s) = (tk+1 , y k+1 , sk+1 ) o valor após o incremento de um passo
α = αk nas direções de Newton já determinadas pela equação (2.26). Assim temos:
t = t + α4t, y = y + α4y, s = s + α4s,
ρ = ρ(t, s),
σ = σ(t, y).
Então:
ρ = (1 − α)ρ + o(α),
σ = (1 − α)σ + o(α),
sT y = (1 − α(1 − δ))sT y + o(α)
onde δ =
mµ
sT y
Um método primal-dual barreira-logarı́tmica (PDBL)
37
Prova Primeiro consideremos ρ:
ρ = s − g(t)
= s + α4s − g(t + α4t)
= s + α4s − g(t) − αA(t)4t + o(α)
= s − g(t) + α(4s − A(t)4t) + o(α)
= (1 − α)ρ + o(α)
A segunda passagem resulta das definições de cálculo, onde temos que o(α) denota
um termo que vai para zero mais rápido que α, ou seja, | o(α)
|→0
α
quando α → 0.
Além disto, observe que a última equação decorre do terceiro bloco de equações do
sistema (2.22). Para σ, a análise é semelhante, sendo que usaremos o primeiro bloco
de equações do sistema (2.22):
σ = ∇f (t) − AT (t)y
= ∇f (t + α4t) − AT (t + α4t)(y + α4y)
= ∇f (t) + α∇2 f (t)4t − AT (t)y − α∇x (y T A(t))T 4t − αAT (t)4y + o(α)
= ∇f (t) − AT (t)y + α(H(t, y)4t − AT (t)4y) + o(α)
= (1 − α)σ + o(α).
Finalmente, analisemos sT y:
sT y = (s + α4s)T (y + α4y)
= sT y + α(sT 4y + 4sT y) + o(α)
(2.30)
Podemos reescrever o termo linear em relação a α assim:
sT 4y + 4sT y = eT (S4y + Y 4s)
= eT (µe − SY e)
= mµ − sT y
(2.31)
= −(1 − δ)sT y.
Substituindo (2.31) em (2.30) nós obtemos o resultado desejado.
¤
Um método primal-dual barreira-logarı́tmica (PDBL)
38
A análise deste teorema permite que percebamos a convergência natural de
ρ, σ para zero ao longo das iterações. Entretanto, a redução de sT y está condicionada
ao fato de δ ∈ (0, 1), ou seja é preciso alterar µ a fim de garantir isto. Para tanto,
seguindo o proposto em [17], é possı́vel tomar µ tal que:
µ=δ
st y
m
onde δ ∈ (0, 1). Desta forma, o valor do produto sT y decrescerá ao longo das iterações.
Por outro lado, a seleção do parâmetro β é fundamental para que as direções
de busca definidas por (2.21) sejam direções de descida para Ψβ,µ . Veremos, a partir
do próximo teorema, as condições a serem buscadas em β para que seja garantido tal
decrescimento desejável.
Teorema 2.6. Suponha que a matriz N definida em (2.25) seja positiva definida.
Então as direções de busca expressas pela equação (2.26) possuem as seguintes propriedades:
(i) Se ρ = 0, então


 
∇t f µ
∇s fµ
 

4t
 ≤0
(2.32)
4s
(ii) Existe βmin ≥ 0 tal que para cada β ≥ βmin ,

 

∇t Ψβ,µ
4t

 
 ≤0
∇s Ψβ,µ
4s
(2.33)
Onde:
βmin =
−(∇f − µAT S −1 e)T N −1 (∇f − µAT W −1 e) + µS −1 ρ + (∇f − µAT S −1 e)T N −1 AT S −1 Y ρ
||ρ||2
Em ambos os casos, a igualdade ocorre se e somente se (t, s) satisfaz (2.21) para algum
y.
Como mencionado anteriormente a prova desse teorema pode ser encontrada
no trabalho de Vanderbei e Shanno [56], onde é proposta a inicialização do algoritmo
Um método primal-dual
39
com β = 0 e este é mantido assim enquanto (4t, 4s) for uma direção de descida
para Ψβ,µ . Quando (4t, 4s) falhar como direção de busca, então β é calculado usando
β = 10βmin a fim de garantir a convergência para um valor mı́nimo da função de mérito
Ψβ,µ .
Logo após a definição do parâmetro de penalidade da função de mérito o passo
αmax será escolhido a partir de um valor que garanta a não negatividade da variáveis
skr e yrk . No nosso caso, isto significa que para r = 1, 2, ...., r0 , skr + α4skr e yrk + α4yrk
serão estritamente positivos se
αmax = 0, 95(max(−
4skr
4yrk
,
−
; r = 1, 2, ..., r0 ))−1
skr
yrk
Então o intervalo [0, αmax ] é pesquisado por sucessivas partições, usando avaliações
da função de penalidade, para valores de α que produzam a redução da função de
penalidade atendendo a condição de Armijo apresentada no anexo A.3. Desta forma é
selecionado o tamanho de passo αpk = αdk .
2.3.2
Um método primal-dual (PD)
O método primal-dual aqui apresentado baseia-se na proposta de Akrotiri-
ankis e Rustem [4], que apresenta uma prova de convergência global para problema
de programação não-linear. Consideremos, um problema de programação não linear
representado por:
M in. f (x)
S.a.
(2.34)
g(x) = 0, x ≥ 0
Neste caso tem-se f (x) : Rn → R e g(x) : Rn → Rm , contı́nua e diferenciável.
Tomemos a aproximação do problema (2.34) dada por
min
f (x) + β2 ||g(x)||2 − µ
Sujeito a: g(x) = 0
Pn
i=1
ln(x)
(2.35)
para β, µ ≥ 0. A função objetivo (2.34) foi acrescida com uma função de
Um método primal-dual
40
penalidade quadrática e uma função de barreira logarı́tmica. A função de penalidade
quadrática aqui usada é a mesma função de mérito apresentada na seção 2.3.1 e é usada
aqui para reforçar a satisfação das restrições de igualdade adicionando um alto custo
na função objetivo a pontos que não sejam factı́veis. A função de barreira logarı́tmica é
introduzida no MPI para garantir a factibilidade estrita enquanto aproxima da solução
ótima.
O método de penalidade/barreira envolve iterações internas e externas. As
iterações externas são associadas com o decrescimento do parâmetro de barreira µ, tal
que µ → 0. As iterações internas determinam o parâmetro de penalidade β e então
resolve o problema (2.35) para determinados valores de µ e β.
As condições de otimalidade para o problema (2.35) são dadas pelo sistema
não linear de equações



∇f (x) − µX −1 e + β∇g(x)T g(x) − ∇g(x)T y
g(x)
 = 0,
Utilizando a transformação não-linear z = µX −1 , obtemos:


∇f (x) − zβ∇g(x)T g(x) − ∇g(x)T y




F (x, y, z; β, µ) =  g(x)
 = 0,


XZe − µe
x>0
x, z > 0.
(2.36)
Para µ fixo, o sistema (2.36) é resolvido pelo método de Newton, onde temos:
H


 ∇g

Z
−∇g T −I
0
0
Onde, H =


0 

X
∇2xx Lβ
4x






 4y  = − 



4z
2
= ∇ f (x) +



 

m
X
∇f − z + β∇g T g − ∇g T y
g




(2.37)
XZe − µe
∇gi (x)(βgi (x) − yi ) + β∇g(x)∇g(x)T . X, Z
i=1
são matrizes diagonais em que os elementos diagonais são respectivamente as coordenadas de x e z. A solução de (2.37) é obtida quando N = H + X −1 Z é inversı́vel, onde
Um método primal-dual
41
temos as seguintes direções:
4x = N −1 (∇g T 4y − ∇f + z − β∇g T g − ∇g T y)
4y = −[∇gN −1 ∇g T ]−1 [g − ∇gN −1 (∇f − z + β∇g T g − ∇g T y)]
4z = −z + µX −1 Z4x
Como no método primal-dual com barreira-logarı́tmica visto na seção (2.3.1),
uma vez que a direção de busca tenha sido definida, o algoritmo processa interativamente determinando novas estimativas para a solução ótima calculando:
xk+1 = xk + αpk 4xk
(2.38)
y k+1 = y k + αdk 4y k
z k+1 = z k + αdk 4z k
O controle do passo é feito de forma a assegurar que as iterações gerem pontos estritamente interiores à região factı́vel e, além disto, o algoritmo move por pontos que
minimizem a função de mérito
n
X
β
ln(x)
Φ = f (x) + ||g(x)||2 − µ
2
i=1
que nada mais é do que a função objetivo do problema (2.35). Este decrescimento,
como no método PDBL é garantido pela adequada seleção do parâmetro β a cada
iteração. Em seu trabalho Akrotiriankis e Rustem [4] demonstra que esta função
decresce monotonicamente e garante a convergência para a solução de (2.36) para
µ fixo. Com a redução de µ, tal que {µ} → 0, é encontrado o valor ótimo para (2.34).
A cada iteração o valor de β é definido de forma a poder garantir o decrescimento da função Φ . Para µ fixo, o gradiente de Φ na k-ésima iteração é 9
∇Φ(xk ; βk , µ) = ∇f + βk ∇gkT gk − µX −1 e
Considerando a segunda equação do sistema de Newton (2.37), a derivada
direcional pode ser escrita como
4xTk ∇Φ(xk ; βk , µ) = 4xTk ∇f (xk ) − βk ||gk ||2 − µ4xTk Xk−1 e
Como o parâmetro µ das iterações internas é fixo, então é possı́vel verificar
que o sinal de ∇Φ(xk ; βk , µ)4xk depende do valor de β. Sendo assim, β é definido
Conclusão
42
como sendo superior a
−1
4xTk ∇fk − µ4xTk XK
e + ||4xk ||2H
||gk ||2
garantindo o decrescimento da função de mérito Φ e, conseqüentemente da
função objetivo do problema original (2.34).
Na seleção do tamanho do passo primal, αp é selecionado conforme a regra de
Armijo (A.3) aplicado à função objetivo a partir de um valor máximo para αpmax =
h
i
xik
min
ξmin 4x
com 0 < ξ < 1.
i <0
|4xi |
k
k
Enquanto o parâmetro de barreira µ é fixo, o passo αd é determinado ao longo
da direção 4zk para cada variável dual zki , i = 1, 2, ..., n, de forma que as seguintes
restrições sejam satisfeitas
αdi = max{α > 0 : Lik ≤ (xik + αp 4xik )(zki + α4zki ) ≤ Uki }
Onde os limites inferior Lik e superior Uki , i = 1, 2, ..., n são definidos como Lik =
min{ 12 mµ, (xik +αp 4xik )zki e Uki = max{2M µ, (xik +αp 4xik )zki }, sendo que os parâmetros
m e M são definidos como:
n (1−γ )(1− γ ) min {xi zi }
i
k
k k
2µ
0 < m < min 1,
µ
o
n
o
maxi {xik zki }
γk ∈ (0, 1)
e M ≥ max 1,
>0
µ
Os valores de m e M são mudados à medida que µ decresce.
O algoritmo primal-dual para programação não-linear aqui descrito encontra
sua prova de convergência global apresentada por Akrotirianakis e Rustem [4] desde
que sejam satisfeitas certas condições. Dentre essas condições, o problema de job-shop
não satisfaz a condição referente a segunda condição de otimalidade. Sendo assim, essa
demonstração não se aplica de forma direta ao nosso caso.
Conclusão
Pela breve descrição do método de pontos interiores feita ao longo deste
capı́tulo é possı́vel perceber a sua importância como ferramenta de resolução de pro-
Conclusão
43
blemas de otimização tanto na forma de programação linear como na forma de programação não linear.
Quanto aos métodos aplicáveis a programação não linear apresentados nas
seções 2.3.1 e 2.3.2, as soluções obtidas para os sistemas (2.36) e (2.17) são as mesmas
significando que os sistemas são equivalentes. Entretanto, estes não são algoritmos de
Newton equivalentes (El-Bakry et al [17], Akrotirianakis e Rustem [4]).
No caso de um problema de job-shop temos duas possibilidades para a sua
modelagem. Como especificado no capı́tulo 1, escolhemos uma modelagem contı́nua de
programação não linear. Neste caso, alguns cuidados deverão ser tomados em função
de se tratar de um espaço de busca não convexo. Vale ressaltar em relação ao método
PDBL que toda discussão em torno da função de penalidade proposta (2.19) assume que
a matriz N seja positiva definida. Entretanto, veremos que não podemos oferecer esta
garantia no caso do problema de job-shop em questão. Será, portanto, preciso fazer
alguma alteração na Hessiana para que possamos garantir a positividade da matriz
N . Veremos, portanto, no próximo capı́tulo como efetuar estas mudanças e quais as
implicações no espaço de busca do primal e do dual.
Capı́tulo 3
Método de Pontos Interiores
Aplicado ao Problema Job-Shop
Como apresentado anteriormente na seção 1.3.3 podemos modelar um problema de seqüenciamento job-shop com uma modelagem contı́nua, mas não linear e
não convexa.
É fato que modelos de programação não linear constituem geralmente um
desafio maior para a busca de soluções (Wright [57]). Entretanto, o método de pontos
interiores, conforme apresentamos na seção 2.3 tem apresentado bons resultados como
ferramenta na busca de soluções de problemas de programação não linear e não convexo
(El-Bakry et al [17], Vanderbei e Shanno [56], Sousa e Costa [53]). Desta forma, a
aparente dificuldade de modelos contı́nuos pode ser superada com o uso de um método
de ponto interior adequado, o que nos levou a adotar neste trabalho um modelo contı́nuo
inspirado na proposta de Pinson [42]. Neste capı́tulo discutiremos em mais detalhes o
modelo contı́nuo para o problema de job-shop adotado na seção 3.1. A seguir na seção
3.2 analisaremos o método de pontos interiores e as alterações que serão necessárias
para usá-lo na resolução do problema de job-shop considerado. Finalmente, faremos na
seção 3.3 uma análise de convergência da metodologia proposta.
Análise do Modelo de Seqüenciamento Job-Shop Adotado
3.1
45
Análise do Modelo de Seqüenciamento Job-Shop
Adotado
No primeiro capı́tulo foi feita uma descrição mais detalhada do problema de
seqüenciamento job-shop (§1.2) e de formas pelas quais é possı́vel construir um modelo
matemático para tal problema (§1.3). O que nos propomos agora é fazer uma análise
mais acurada do modelo matemático não linear apresentado na seção (§1.3.3). Este
modelo foi adotado em nosso trabalho pelos motivos mencionados anteriormente no
capı́tulo 1, e por outros motivos que se evidenciarão ao longo de nossas análises nas
seções seguintes. Relembrando as definições feitas nestas seções (§1.2, §1.3.3), podemos
descrever um problema de seqüenciamento job-shop com m
e máquinas e p produtos como
um problema de otimização restrito da forma:
M in.
f (t) =
n0
X
tj
j=1
S.a.
tj+1 − tj − dj ≥ 0 ∀j ∈ C
−(tv − tu + dv ) × (tu − tv + du ) ≥ 0 ∀(u, v) ∈ D
(3.1)
tj ≥ 0 j = 1, ..., p0
B − tj ≥ 0 j = 1, ..., p0
Fizemos uma mudança de sinal nas restrições tornando-as não negativas para
adequar ao modelo padrão de programação não linear em que estaremos aplicando o
método de pontos interiores. Além disto, incluı́mos um limite superior B às variáveis
do problema. Este limite superior apenas serve como garantia de que se trata de um
espaço de busca limitado facilitando demonstrações de teoremas subseqüentes. Vale
ressaltar que essa alteração não altera em nada a solução do problema original. O
n0
X
calculo desse limite foi feito tomando-se B =
dj + 1 que é um valor superior ao
j=1
tempo de inı́cio de qualquer operação na pior de todas as hipóteses.
Consideremos R = {r = 1, ..., r0 } como sendo um conjunto de ı́ndices referentes a cada restrição. Sendo assim, observe que nosso modelo foi dividido em quatro
grupos de restrições. O primeiro, terceiro e quarto grupo de restrições são lineares e
Análise do Modelo de Seqüenciamento Job-Shop Adotado
46
referindo-se respectivamente às restrições conjuntivas ou de precedência na gama operatória, às restrições de não negatividade das variáveis e ao limite superior imposto às
variáveis. A segunda restrição é onde se centraliza nossa principal atenção e refere-se
aos pares de restrições disjuntivas. Este grupo de inequações não é linear e além disto
introduz uma componente não conexa em nosso espaço de busca de soluções. Vamos,
portanto, analisar um pouco melhor este grupo de restrições. Consideremos a seguinte
função:
g(tu , tv ) = −(tv − tu + dv ) × (tu − tv + du )
Fazendo as devidas multiplicações podemos reescrevê-la assim:
g(tu , tv ) = t2u + t2v − 2tu tv + (du − dv )tu + (dv − du )tv − dv du
3.1.1
(3.2)
Análise do Espaço de Busca
Vamos primeiramente verificar o espaço de busca referente a uma disjunção.
Neste caso estamos procurando pontos para os quais g(tu , tv ) ≥ 0. Este conjunto de
pontos para uma restrição é apresentado na figura 3.1 , onde podemos verificar que o
espaço de busca referente à disjunção não é conexo como mencionado anteriormente
(1.3.3). Este fato condiz com a caracterı́stica combinatória do seqüenciamento jobshop. Caso escolhamos uma direção para a disjunção estaremos definindo o lado no
espaço de busca. Neste caso, se escolhermos primeiro executar a operação u e depois
a operação v, então estaremos escolhendo o região A1 na figura 3.1. Por outro lado,
se escolhermos inverter a ordem das operações então estaremos escolhendo pontos na
região A2 da figura 3.1.
Note que a função g apresentada
na equação (3.2) é duplamente diferenciável

2 −2
. Considerando um vetor t = (tu , tv ) ∈ <2
e sua matriz Hessiana é H = 
−2
2
T
temos que t Ht é:
2t2u − 4tu tv + 2t2v = 2(tu − tv )2 ≥ 0
Então, podemos dizer que a função g é convexa pois a matriz Hessiana desta
função é semi-definida positiva para todos os pontos de seu domı́nio. Para confirmar
isto veja um exemplo do gráfico desta função na figura 3.2.
Análise do Modelo de Seqüenciamento Job-Shop Adotado
47
tv
A1
du
A2
tu
dv
Figura 3.1: Gráfico que representa a região de busca referente a uma restrição disjuntiva
100
80
60
z
40
20
0
0
1
−20
2
3
−40
4
0
1
5
2
3
6
4
5
y
7
6
8
7
8
9
9
10
x
10
Figura 3.2: Gráfico da função que representa uma restrição disjuntiva
Análise do Modelo de Seqüenciamento Job-Shop Adotado
48
Observação 3.1. O fato da função g ser convexa traz implicações importantes neste
caso, pois como vimos nesta seção temos um espaço de busca não convexo. Diante
disto, pelo teorema A.6 apresentado em anexo, concluı́mos que para o problema 3.1 um
ponto que atenda as condições de KKT do teorema A.4 tendo uma restrição disjuntiva
ativa não será necessariamente um ponto onde a função objetivo é mı́nima.
Vamos tomar como exemplo um problema de job-shop contendo apenas dois
produtos e três operações. Este exemplo servirá não só para confirmar a observação
3.1, bem como para apresentar outros aspectos importantes referentes ao problema.
Consideremos então um problema de job-shop com dois produtos e duas maquinas,
cujos dados são apresentados na tabela 3.1.
produto
operação
duração
máquina
1
1
3
1
1
2
5
2
2
3
7
2
Tabela 3.1: Dados do problema-exemplo 2 de job-shop.
Após a modelagem adequada temos,
M in. f (t) = t1 + t2 + t3
S.a.
t2 − t1 − 3 ≥ 0
t22 + t23 − 2t2 t3 + 2t3 − 2t2 − 35 ≥ 0
t1 ≥ 0
t2 ≥ 0
(3.3)
t3 ≥ 0
16 − t1 ≥ 0
16 − t2 ≥ 0
16 − t3 ≥ 0
Para este problema temos dois pontos (t1 = (0, 3, 8) e t2 = (0, 7, 0)) satisfazendo a primeira condição de otimalidade (KKT) e tendo pelo menos uma restrição
disjuntiva ativa. Estes pontos são exatamente as duas únicas possibilidades referentes à única restrição disjuntiva. O ponto t1 é obtido quando executamos primeiro a
operação 2 na máquina 2 e, o ponto t2 refere-se a execução da operação 3 antecedendo a
Análise do Modelo de Seqüenciamento Job-Shop Adotado
49
operação 2 na máquina 2. Entretanto, t2 é um ponto onde a função objetivo é mı́nima
(f (t2 ) = 7) enquanto para t1 temos f (t1 ) = 11 não sendo a melhor opção.
Uma outra observação importante decorrente deste problema refere-se ao fato
de que plano tangente a estes pontos é composto apenas pelo vetor nulo. Portanto,
não é possı́vel concluir nada quanto a otimalidade dos pontos estacionários referentes
a este problema. Isto nos leva a uma análise da Hessiana do Lagrangeano H(t, y) pois,
além destes motivos aqui mencionados, para atender a condição de otimalidade de
segunda ordem, é preciso que H(t, y) seja positiva definida no hiperplano formado pelos
gradientes das restrições ativas. Vejamos, então qual o comportamento da Hessiana
H(t, y) para o problema de job-shop aqui considerado.
3.1.2
Análise da Hessiana do Lagrangeano
Retomemos o modelo matemático empregado no inı́cio desta seção e reescre-
vamos os blocos de restrições como funções duplamente diferenciáveis expressas por:
1
gj,j+1
(t) = tj+1 − tj − dj
j∈C
2
gu,v
(t)
= t2u + t2v − 2tu tv + (du − dv )tu + (dv − du )tv − dv du
(u, v) ∈ D
gj3 (t)
= tj
j ∈ J = 1, ..., p0
gj4 (t)
= B − tj
j ∈ J = 1, ..., p0
Assim podemos reescrever o Lagrangeano do problema de job-shop apresentado
na equação 2.15, levando em consideração estes três blocos de restrições.
L(t, s, y) = f (t)−µln s−(y 1 )T (g 1 (t)−s1 )−(y 2 )T (g 2 (t)−s2 )−(y 3 )T (g 3 (t)−s3 )−(y 4 )T (g 4 (t)−s4 )
A matriz Hessiana H(t, y) será portanto composta pela soma da hessiana da
função f (t) e das hessianas de todas as r restrições do problema. A função f (t) e as
restrições que compõem o primeiro, terceiro e quarto grupo de restrições são lineares,
então suas respectivas hessianas são matrizes nulas. Concluı́mos assim, que a Hessiana
H(t, y) = −(y 2 )T G2 (t), onde G2 (t) representa a soma das hessianas do segundo grupo
de restrições que corresponde ao grupo das restrições disjuntivas.
Análise do Modelo de Seqüenciamento Job-Shop Adotado
50
As matrizes hessianas deste segundo grupo de equações terão um formato em
bloco semelhante entre si. Em cada bloco temos que
∂ 2g2
∂ 2g2
=
=
∂t2u
∂t2v
2
(u, v) ∈ D
∂ 2g2
∂ 2g2
=
= −2
∂tu tv
∂tv tu
(u, v) ∈ D
∂ 2g2
∂ 2g2
=
=
∂tu tv
∂tv tu
(u, v) 6∈ D
0
Logo, cada hessiana destas restrições será uma matriz simétrica com a diagonal composta de dois termos iguais a 2 e dois outros termos simétricos iguais a −2 referentes
a disjunção considerada e os demais termos são nulos. Como a Hessiana H(t, y) é
composta da soma das hessianas das restrições pré-multiplicadas por −yr1 e, sendo
yr > 0 conforme a observação 2.1, então H(t, y) será composta de blocos de matrizes
semi-definidas negativas. Assim podemos concluir que H(t, y) é semi-definida negativa.
Para explicitar estas principais caracterı́sticas da Hessiana tomemos um novo
exemplo de job-shop, apresentado pela tabela abaixo:
produto
operação
duração
máquina
1
1
4
1
1
2
5
2
2
3
3
1
2
4
2
2
3
5
5
1
Tabela 3.2: Dados do problema-exemplo 3 de job-shop.
Análise do Modelo de Seqüenciamento Job-Shop Adotado
51
Após a modelagem matemática proposta, temos:
Min.:
5
X
tj − µ
j=1
16
X
ln sr
r=1
Sujeito a: t2 − t1 − 4 − s1 = 0
t4 − t3 − 3 − s2 = 0
t21 + t23 − 2t1 t3 + t1 − t3 − 12 − s3 = 0
t23 + t25 − 2t3 t5 − 2t3 + 2t5 − 15 − s4 = 0
t21 + t25 − 2t1 t5 − t1 + t5 − 20 − s5 = 0
t22 + t24 − 2t2 t4 + 3t2 − 3t4 − 10 − s6 = 0
t1 − s7 = 0
t2 − s8 = 0
t3 − s9 = 0
t4 − s10 = 0
t5 − s11 = 0
19 − t1 − s12 = 0
19 − t2 − s13 = 0
19 − t3 − s14 = 0
19 − t4 − s15 = 0
19 − t5 − s16 = 0
Neste caso, já foram incluı́das as variáveis de excesso e uma função de barreira logarı́tmica a fim de obter restrições de igualdade e garantir não negatividade destas
novas variáveis introduzidas. Se considerarmos os multiplicadores de Lagrange como
sendo yr , r ∈ R = 1, ..., 11, então a Hessiana H(t, y) será dada por:

−2y3 − 2y5
0
2y3
0
2y5



0
−2y6
0
2y6
0


H(t, y) = 
2y3
0
−2y3 − 2y4
0
2y4



0
2y6
0
−2y6
0

2y5
0
2y4
0
−2y4 − 2y5











Consideremos um vetor genérico t = (t1 , t2 , t3 , t4 , t5 ) t ∈ R5 , então fazendo tT H(t, y)t
e lembrando que o valor de yr ≥ 0, obtemos:
−2y3 (t1 − t3 )2 − 2y4 (t3 − t5 )2 − 2y5 (t1 − t5 )2 − 2y6 (t2 − t4 )2 ≤ 0
∀t ∈ R5
Análise do Modelo de Seqüenciamento Job-Shop Adotado
52
Logo H(t, y) é semi-definida negativa para quaisquer vetores do R5 . Isto indica que os
pontos estacionários obtidos para um problema de job-shop ou são pontos de máximo
local ou não se pode afirmar nada a respeito deles como aconteceu no problema-exemplo
2.
O método de pontos interiores faz uma busca procurando pontos que atendam
a primeira condição de otimalidade, ou seja, busca-se pontos estacionários. Portanto,
é preciso guiar esta busca para garantir a convergência para pontos onde a função
objetivo seja mı́nima. Esta orientação na busca é feita através do uso de funções de
mérito de forma semelhante ao apresentado nas seções 2.3.2 e 2.3.1. Nesta última seção,
através do teorema 2.6 nós mostramos que a direção de busca obtida pelo algoritmo
PDBL (4t, 4s) tem caracterı́sticas decrescentes tanto para a função de barreira como
para função de mérito usada desde que N (t, y, s) = H(t, y) + (A(t))T S −1 Y A(t) seja
positiva definida. Caso isto não ocorra, o algoritmo pode até convergir, mas pode
caminhar para um ponto onde a solução não seja mı́nima.
No nosso caso, já que as variáveis si e yi são positivas então (A(t))T S −1 Y A(t)
é definida positiva desde que a matriz Jacobiana do Lagrangeano A(t) tenha posto
completo o que é verdade em nosso caso particular. Entretanto, não podemos garantir
que a matriz N (t, y, s) seja definida positiva a cada iteração em função da Hessiana
H(t, y) ser semi-definida negativa como acabamos de ver. A saı́da encontrada continua
sendo semelhante a apresentada na seção 2.3.1. No caso de N (t, y, s) não ser definida
e y) = H(t, y) + λI. Esta mudança, garante
positiva então substituı́mos H(t, y) por H(t,
que serão encontradas direções de decrescimento para as funções de mérito usadas e
conseqüentemente para a função objetivo do problema original. Entretanto, mesmo
tendo sido alteradas apenas as informações de segunda ordem, é preciso analisar qual
o impacto provocado na convergência do algoritmo. Esta análise será feita na seção
seguinte.
Método de Pontos Interiores e o Seqüenciamento Job-Shop
3.2
53
Método de Pontos Interiores e o Seqüenciamento Job-Shop
Como visto na seção 3.1 o modelo de programação matemática adotado para
o problema de seqüenciamento job-shop é um modelo de programação não linear e não
convexo. O método de pontos interiores tem sido usado com sucesso em situações desta
natureza (seção 2.3), entretanto alguns cuidados deverão ser tomados a fim de garantir
a convergência neste caso particular. Retomaremos as definições referentes ao método
de pontos interiores com barreira logarı́tmica vistas na seção 2.3.1, buscando realizar
os ajuste necessários à convergência do método ao ser aplicado ao nosso problema de
job-shop.
Lembremos que um problema de job-shop possui tantas variáveis quanto o
número de operações, ou seja, n0 variáveis. Se, então, denotarmos por r0 o número
total de restrições, podemos definir uma função g(t) : Rp0 → Rr0 para representar as
restrições do problema de job-shop da seguinte forma:

t − dj − tj
 j+1
 2
 tu + t2v − 2tu tv + (du − dv )tu + (dv − du )tv − dv du
g(t) = 

 tj

B − tj
sendo: j ∈ C








(3.4)
(u, v) ∈ D
j = 1, ..., p0
P0
B = pj=1
dj
Desta forma o problema 3.1 pode ser reescrito como um modelo geral de programação não linear:
M in. f (t)
S.a.
(3.5)
g(t) ≥ 0
Neste caso o vetor t possui dimensão p0 e as funções f (t) =
p0
X
tj e g(t) definida em
j=1
(3.4) são duplamente diferenciáveis. Acrescentamos uma variável de folga sr em cada
uma das r restrições de desigualdade com a finalidade de transformá-las em igualdade.
Método de Pontos Interiores e o Seqüenciamento Job-Shop
Incorporamos, também, uma função de barreira logarı́tmica Bµ = µ
54
r0
X
ln si à função
i=1
objetivo para garantir a positividade desta nova variável. Assim obtemos:
M in. f (t) − µ ln s
S.a.
g(t) − s = 0
(3.6)
As condições de otimalidade de primeira ordem (KKT) para o problema (3.6)
são:
∇t L(t, s, y) = ∇f (t) − (A(t))T y = 0
∇s L(t, s, y) = −µe + SY e = 0
(3.7)
∇y L(x, s, y) = (g(t) − s) = 0
onde
A(t) =
∂g(t)
∂t
que é a matriz Jacobiana de g(t)
S é uma matriz diagonal contendo as variáveis de folga sr ;
Y é uma matriz contendo na diagonal os elementos yr ;
e = (1, ..., 1);
∇t f (t) = (1, ..., 1).
3.2.1
Definições iniciais e funções de mérito
Antes de descrever o método de pontos interiores utilizado gostarı́amos de
relembrar algumas notações já usadas no capı́tulo anterior e que serão retomadas aqui:
σ = ∇f (t) − A(t)T y
γ = µS −1 e − y
ρ = −g(t) + s
(3.8)
p(t, s); z = (p, y) = (t, s, y)
Além destas definições, com o objetivo de guiar a um caminho de busca por
direções que garantam o decrescimento da função objetivo, estaremos utilizando algumas funções de mérito à semelhança do que foi realizado nos algoritmos apresentados
Método de Pontos Interiores e o Seqüenciamento Job-Shop
55
na seção 2.3. Definiremos as seguintes funções de mérito:
ν(t, s, y)
= max{||σ||, ||ρ||, ||SY e||}
νµ (t, s, y)
= max{||σ||, ||ρ||, ||Sγ||}
r0
X
β
ln si + y T ρ + ρT ρ
Lβ,µ (t, s, y) = f (t) − µ
2
i=1
Estaremos adotando em nossas análises a norma l∞ ou seja se t ∈ Rp0 então
||t|| = max |xi |. Desta forma, note que a função ν(t, s, y) mede a distância entre a
1≤i≤p0
aproximação corrente e pontos estacionários (KKT) para o problema 3.5. Já a função
νµ (t, s, y) mede a distância entre o ponto corrente e pontos estacionários para o problema com barreira 3.6 tendo µ fixo.
Gostarı́amos de dar uma atenção especial à função Lβ,µ (t, s, y) que é o Lagrangeano aumentado para o problema com barreira 3.6. O Lagrangeano aumentado pode
ser visto como uma função de penalidade exata quando os próprios valores duais yr são
usados nas iterações [34].
De forma semelhante aos métodos clássicos de otimização que utilizam o Lagrangeano aumentado inicializaremos com um determinado vetor y de variáveis duais e
buscaremos através do MPI encontrar um ponto pk = (tk , sk ) que minimize Lβ,µ (t, s, y).
Em seguida alteraremos o vetor de variáveis duais tomando y = y + βρ(t, s).
Como estamos tratando com um problema cujo espaço de busca não é convexo
o Lagrangeano aumentado é uma boa opção a ser usada como função de penalidade
(mérito) na medida em que este possui um ponto de sela na solução ótima do primal,
mesmo diante de falta de convexidade [36]. Entretanto, para que isto aconteça é preciso
que Lβ,µ (t, s, y) seja limitado inferiormente, esta análise será feita na seção 3.3 através
do teorema 3.2. Mostraremos também, que as mudanças propostas na seção 3.2.2
garantirão que a direção primal encontrada pelo MPI é uma direção de decrescimento
para a função Lβ,µ (t, s, y).
Feitas estas colocações aplicaremos o método de Newton a este conjunto de
Método de Pontos Interiores e o Seqüenciamento Job-Shop
equações (3.7) o que nos fornecerá

H(t, y) 0 −A(t)T



0
Y
S

A(t) −I
0
Onde H(t, y) = ∇2 f (t)−
P
r
o seguinte sistema linear:
 


4t
−∇f (t) + A(t)T y
 


 


  4s  = 
µe − SY e
 


4y
−g(t) + s
56





(3.9)
yr ∇2t gr (t) e representa a matriz Hessiana do Lagrangeano.
Se considerarmos N (t, y, s) = H(t, y)+A(t)T S −1 Y A(t) como sendo uma matriz
inversı́vel, então podemos definir de forma explı́cita as direções de busca encontradas
pelo MN como:
4t = N −1 (−σ + AT (S −1 Y ρ + γ))
(3.10)
4s = −ρ − A4t
4y = γ + S −1 Y (ρ − A4t)
Os cálculos aqui foram omitidos, mas o processo é semelhante ao apresentado
pelo teorema 2.4.
3.2.2
Mudança da matriz normal N (t, s, y)
Para aplicar o MPI ao problema de job-shop precisamos que a matriz N (t, s, y)
seja inversı́vel em função do teorema 2.4, mas isto não é suficiente. Precisamos que
esta matriz N (t, s, y), que denominaremos de matriz normal, seja uma matriz definida
positiva para que possamos garantir direções de busca decrescentes para a função de
mérito associada ao método (veja teorema 2.6). Entretanto, a matriz N (t, y, s) pode
não ser definida positiva pelo fato da Hessiana H(t, y) ser semi-definida negativa como
apresentado na seção 3.1.2. Neste caso, podemos alterar esta matriz N fazendo:
b (t, y, s) = N (t, y, s) + λI,
N
λ≥0
(3.11)
A nossa preocupação se volta para a Hessiana H(t, y) visto que A(t)T S −1 Y A(t)
é semi-definida positiva, pois as variáveis s e y são assumidas sendo positivas. Assim
o incremento de uma constante λ aos elementos diagonais feitas pela equação (3.11)
alterará basicamente a Hessiana H(t, y). Desta forma, as informações de segunda
ordem do sistema de equações original (2.13) é aproximada sendo que as informações de
Método de Pontos Interiores e o Seqüenciamento Job-Shop
57
primeira ordem permanecem intactas. Sobretudo, se λ é incrementado até que N seja
definida positiva, então poderemos aplicar o teorema 2.6 e garantir o decrescimento
tanto para a função de mérito como para a função de barreira. Mas, tal mudança
certamente produz algum impacto no espaço de busca primal e/ou do dual. O teorema
b = H(t, y) + λI,
3.1 verifica esta questão, considerando a matriz H
λ > 0 no lugar
de H à medida que verifica a variação do lado direito do sistema (3.9) ao longo das
iterações. Antes de ver este teorema, lembremos que o algoritmo de MPI realiza passos
(t, s, y) → (e
t, se, ye) tais que
e
t = t + α4t
se = s + α4s
ye = y + α4y
Consideremos inicialmente α como sendo um tamanho de passo único tanto para o
primal como para o dual. O tamanho de passo é definido, como mencionado anteriormente na seção 2.3.1, de forma que a variável dual y e de folga s sejam estritamente
positivas, ou seja:
i
h
α = ξmin
min
sr
,
4sr <0 |4sr |
min
yr
,
4yr <0 |4yr |
1.0
onde 0 < ξ < 1.
Teorema 3.1. Considere (e
t, ye, se) como sendo o valor das variáveis (t, y, s) após um
passo nas direções de Newton definidas pela equação (3.10). Assim temos:
e
t = t + α4t, ye = y + α4y, se = s + α4s,
ρe = ρ(e
t, se),
σ
e = σ(e
t, ye).
Substituindo H por H = H + λI, λ ≥ 0, tem-se:
ρe = (1 − α)ρ + o(α),
seT ye = (1 − α(1 − δ))sT y + o(α),
com δ =
r0 µ
sT y
σ
e = (1 − α)σ − αλ4t + o(α).
Prova: Os dois primeiros ı́tens não sofrem nenhuma alteração em função da mudança
da Hessiana, tendo demonstração igual a realizada no teorema 2.5.
Método de Pontos Interiores e o Seqüenciamento Job-Shop
58
Para σ
e, a análise é semelhante a feita no teorema 2.5, sendo que usaremos a
b no lugar de H:
matriz H
σ
e = ∇f (e
t) − AT (e
t)e
y
= ∇f (t + α4t) − AT (t + α4t)(y + α4y)
= ∇f (t) + α∇2 f (t)4t − AT (t)y − α∇x (y T A(t))T 4t − αAT (t)4y + o(α)
= ∇f (t) − AT (t)y + α(H(t, y)4t − AT (t)4y) + o(α)
Substituindo H por H , temos
σ
e = ∇f (t) − AT (t)y + α((H(t, y) + λI)4t − AT (t)4y) + o(α)
= ∇f (t) − AT (t)y + α((H(t, y)4t − AT (t)4y) + λ4t) + o(α)
= (1 − α)σ − αλ4t + o(α).
¤
O teorema 3.1 mostra que a alteração realizada com o incremento de um fator
λ nos elementos da diagonal de N (t, y, s) não tem nenhum impacto na factibilidade
do primal (ρ), mas possui uma interferência na factibilidade do dual. Neste caso,
se λ for maior que zero, a infactibilidade do dual pode deixar de decrescer mesmo
com passos arbitrariamente pequenos. Diante deste fato relevante no caso do job-shop,
buscamos uma regularização do dual conforme Griva et al [28]. Acrescentamos um novo
parâmetro ² para controlar o crescimento das variáveis duais. Estaremos admitindo
² =
1
β
onde β é o parâmetro de penalidade da função Lβ,µ (t, s, y). O motivo desta
escolha ficará evidente na seção 3.3. Desta

H(t, y)
0
−A(t)T



0
S −1 Y
I

1
A(t)
−I
I
β
forma o sistema (3.9) será reescrito como:



 
−σ
4t



 



 
(3.12)
  4s  =  γ 



 
ρ
4y
Substituindo ² por df rac1β, temos:





 
H(t, y)
0
−A(t)
0
S −1 Y
I
A(t)
−I
1
I
β
T






−σ
4t






 4s  =  γ



ρ
4y





(3.13)
Método de Pontos Interiores e o Seqüenciamento Job-Shop
59
O teorema seguinte apresenta não apenas uma condição necessária para que
este sistema tenha solução definida, como também, fórmulas explı́citas para obtenção
das direções de busca.
Teorema 3.2. Seja Nβ (t, y, s) = H(t, y) + A(t)T [SY −1 + β −1 I]−1 A(t) uma matriz não
singular, então o sistema (3.13) tem solução única e, particularmente temos:
4t = Nβ−1 (βAT (S −1 Y + β)−1 (γ − βρ) − σ + βAρ)
4s = (S −1 Y + β)−1 (γ − βρ + βA4t)
(3.14)
4y = β(ρ − A4t + 4s)
Prova:
Primeiramente resolvemos a terceira equação do sistema 3.13 para 4y onde
obtivemos
4y = β(ρ − A4t + 4s)
a seguir substituı́mos 4y na primeira e segunda equação. Desta forma obtemos o
seguinte sistema na forma matricial:

 



H + βAT A
−βAT
4t
−σ + βA(t)T ρ

 
 = 

−1
−βA
S Y + βI
4s
γ − βρ
(3.15)
Observe que o sistema (3.15) é um sistema simétrico. Para resolução deste sistema
primeiro resolvemos a segunda equação para 4s, obtendo:
4s = (S −1 Y + β)−1 (γ − βρ + βA4t)
em seguida substituı́mos esta expressão na primeira equação, assim temos:
(H + βAt A − βAt (S −1 Y + β)βA)4t = βAT (S −1 Y + β)−1 (γ − βρ) − σ + βAρ
Observe que:
H + βAt A − βAt (S −1 Y + β)−1 βA = H + βAT A(1 − βs(Y e + βs)−1 )
= H + βY AT (Y e + βS)−1 A
= H(t, y) + A(t)T [SY −1 + β −1 I]−1 A(t) = Nβ (t, s, y)
Desta forma, se Nβ for não singular então obtemos:
4t = Nβ−1 (βAT (S −1 Y + β)−1 (γ − βρ) − σ + βAρ)
Método de Pontos Interiores e o Seqüenciamento Job-Shop
60
¤
Como fizemos anteriormente, exigiremos um pouco mais de Nβ (t, y, s). Precisamos que a matriz Nβ seja positiva definida. Caso isto não aconteça, nós a substituı́mos por
bβ (t, y, s) = Nβ (t, y, s) + λI,
N
λ≥0
(3.16)
Neste caso, λ é incrementado até que o menor autovalor de Nβ seja maior que um
determinado λN > 0. Antes de apresentarmos a forma de fazer este incremento em Nβ
veremos uma conseqüência interessante pelo fato de torná-la definida positiva. Neste
caso, além de podermos garantir a solução para o sistema (3.13), poderemos pelo
teorema 3.3 garantir que a matriz reduzida (3.15) também é positiva definida
Teorema 3.3. Consideremos as matrizes Nβ = H +AT [β −1 I +Y −1 S]−1 A e S −1 Y +βI
sendo matrizes simétricas e positivas definidas com menores auto-valores sendo λN e
λC respectivamente. Então a matriz


T
T
H + βA A
−βA

M =
−βA
S −1 Y + βI
é também positiva definida com menor autovalor λM dependendo de λN e λC .
Prova: Precisamos mostrar que para qualquer vetor p = (t, s) 6= 0 a forma quadrática
pT M p é positiva. Na demonstração do teorema 3.2 vimos que
Nβ = H + AT [β −1 I + Y −1 S]−1 A = H + βAt A − βAt (S −1 Y + β)−1 βA
Como a matriz Nβ é positiva definida temos que:
tT (H + βAT A − βAt (S −1 Y + βI)−1 βA)t ≥ λ0 tT t
tT (H + βAT A)t − tT βAt (S −1 Y + βI)−1 βA)t ≥ λ0 tT t
tT (H + βAT A)t ≥ tT βAt (S −1 Y + βI)−1 βA)t + λ0 tT t
Portanto
h
i
tT sT




T
T
H + βA A
−βA
−βA
S −1 Y + βI

t
s
=
= tT (H + βAT A)t + sT (S −1 Y + βI)t − 2sT (βA)t ≥
≥ tT βAt (S −1 Y + βI)−1 βA)t + λN tT t + sT (S −1 Y + βI)t − 2sT (βA)t =
= λN tT t + (S −1 Y + βI)−1 ((S −1 Y + βI)s − βAt)2 ≥ λM pt p
Método de Pontos Interiores e o Seqüenciamento Job-Shop
61
onde λM ≥ α min{λN , λC }, α > 0.
¤
Como as variáveis s, y e o parâmetro β são assumidos sendo positivos, então
S −1 Y + βI será definida positiva e podemos admitir λC = β.
Por outro lado, a matriz Nβ poderá não ser definida positiva visto que a
Hessiana H(t, y) é definida negativa conforme análise feita na seção 3.1.2. Em função
disto buscaremos tornar a matriz Hessiana definida positiva tendo como conseqüência
a positividade da matriz Nβ já que [AT (β −1 I + Y S −1 )−1 A] já é positiva definida.
A matriz hessiana possui todos os elementos da diagonal como valor definido
X
yr , onde Di é o conjunto de multiplicadores de lagrange referentes às
como −2
r∈Di
restrições disjuntivas associadas a operação i. Como os multiplicadores de Lagrange
são variáveis não negativas então teremos os elementos diagonais sempre negativos.
Portanto, selecionamos uma constante positiva λ que possa tornar estes elementos
diagonais positivos pela substituição de H(t, y) por H(t, y) = H(t, y) + λI. Tomamos,
então λ = 2| min hii |, assim a menor entrada diagonal de H(t, y) terá o valor de
1≤i≤no
P
2 i∈Di yr . Como as entradas fora da diagonal possuem valor igual a 2yr esta mudança
é o suficiente para garantir a positividade de H = H(t, y) + λI. Esta adaptação é
possı́vel em função de todas as entradas não nulas serem múltiplas de 2. Assim, o que
fizemos foi transformar a menor entrada diagonal num múltiplo não negativo de 2.
O efeito desta mudança pode ser observado tomando-se a matriz Hessiana do
problema exemplo 3 onde temos:

−2y3 − 2y5
0
2y3
0
2y5



0
−2y6
0
2y6
0


H(t, y) = 
2y3
0
−2y3 − 2y4
0
2y4



0
2y6
0
−2y6
0

2y5
0
2y4
0
−2y4 − 2y5











Método de Pontos Interiores e o Seqüenciamento Job-Shop
Supondo arbitrariamente os valores das variáveis duais sendo y

−16 0
6
0
10


 0 −12 0
12
0


H(t, y) =  6
0 −14 0
8


 0
12
0 −12 0

10
0
8
0 −18
62
= (1, 2, 3, 4, 5) teremos:











Neste caso, a menor entrada diagonal é h55 = −18, tomando λ = 2| − 18| = 36 teremos
H(t, y) sendo:


20 0 6 0 10


 0 24 0 12 0


H(t, y) =  6 0 22 0 8


 0 12 0 24 0

10 0 8 0 18










Consideremos um vetor genérico t = (t1 , t2 , t3 , t4 , t5 ) t ∈ R5 , então fazendo tT H(t, y)t,
obtemos:
6(t1 + t3 )2 + 8(t3 + t5 )2 + 10(t1 + t5 )2 + 12(t2 + t4 )2 + 8t23 + 4t21 + 12t22 + 12t24 ≥ 0
∀t ∈ R5
Desta forma podemos garantir que a matriz H(t, y) é definida positiva. Entretanto, este acréscimo diagonal (λ = 4| min hii |) pode ser excessivo, fazemos então,
1≤i≤no
uso da decomposição de Cholesky para poder obter a menor perturbação possı́vel que
garanta a positividade da matriz Normal Nβ . Multiplicamos então o valor de λ por
um fator 0 < ξ < 1 de forma crescente até poder completar a decomposição Cholesky
tendo na diagonal apenas elementos estritamente positivos. Um algoritmo sugestivo
para esta mudança é apresentado no anexo B.1.
3.2.3
Um algoritmo de pontos interiores aplicado ao seqüenciamento job-shop
Nesta seção apresentaremos alguns detalhes relativos a adaptação do método
de pontos interiores à resolução de um problema de seqüenciamento job-shop como nos
Método de Pontos Interiores e o Seqüenciamento Job-Shop
63
propomos a fazer. Para melhor compreensão dos ı́tens apresentados estaremos utilizando como ilustração dos passos mencionados o problema-exemplo 2. Transcrevemos
mais uma vez a tabela descritiva de seus dados e a modelagem matemática adotada a
fim de facilitar a posterior análise. Assim temos:
produto
operação
duração
máquina
1
1
3
1
1
2
5
2
2
3
7
2
Tabela 3.3: Dados do problema-exemplo 2 de job-shop.
Após a modelagem adequada temos,
M in. f (t) = t1 + t2 + t3
S.a.
t2 − t1 − 3 ≥ 0
t22 + t23 − 2t2 t3 + 2t3 − 2t2 − 35 ≥ 0
t1 ≥ 0
t2 ≥ 0
(3.17)
t3 ≥ 0
16 − t1 ≥ 0
16 − t2 ≥ 0
16 − t3 ≥ 0
A resolução dos ı́tens que se seguirão foi realizada com o uso do Scilab 3.0, que é um
aplicativo matemático de uso livre.
3.2.3.1
Ponto de partida e parâmetros iniciais
A determinação de um ponto de partida neste método é um aspecto impor-
tante. Nota-se que é preciso garantir a factibilidade do ponto escolhido mas isto não
é o suficiente. A tabela 3.4 apresenta resultados obtidos para a função objetivo após
1 e 20 iterações ao ser aplicado o MPI a alguns pontos. Tais pontos foram tomados
a partir de uma escolha particular da direção dos arcos disjuntivos, que neste caso foi
escolhido realizar a operação 3 e depois a operação 2 na máquina 2.
Observa-se que os resultados ao longo das iterações difere mesmo para pontos
Método de Pontos Interiores e o Seqüenciamento Job-Shop
64
Ponto inicial
primeira iteração
20 iterações
Variação
Tipo de ponto
(1,9,2)
11,08
14,36
+ 3,28
Factı́vel
(1,9,1)
10,54
10,05
-0,49
Est. factı́vel
(3,10,3)
14,62
12,9
-1,66
Factivel
(3,14,4)
20,6
20,18
-,42
Infavtı́vel
(2,10,3)
13,6
11,83
-1,77
Factı́vel
Tabela 3.4: Análise ponto inicial
factı́veis. Alguns pontos possuem uma grande variação na primeira iteração, mas tal
comportamento não é constante. Portanto, a escolha do ponto inicial é importante no
desenvolvimento do MPI.
Uma outra necessidade é a definição das variáveis de excesso s. Por definição
podemos obter tais variáveis admitindo gr (t)geq0 e lembrando que é preciso que se
tenha gr (t) − s = 0, com s > 0. Assim, note que as variáveis de excesso podem ser
computadas tomando s0r = gr (t0 ). Por segurança para evitar pontos muito próximos
ou contidos nas bordas da região factı́vel tomaremos as variáveis de excesso como:
s0r = gr (t0 + θ) onde θ > 0
Dessa forma, teremos as variáveis de excesso estritamente positivas. Nota-se que, a
variação do parâmetro θ exerce influencia nos resultados e deve ser escolhida com
cuidado.
Após a definição das variáveis primais, deveremos definir valores para as variáveis
duais. A computação dessas variáveis precisa ser feita de forma que tenhamos
A(t0 )T y − ∇f (t0 ) = 0
atendendo a primeira condição de otimalidade, como preconiza o método de pontos
interiores. Sendo assim, obtemos o valor das variáveis duais resolvendo o sistema
representado pela seguinte equação
A(t0 )T y = ∇f (t0 )
(3.18)
Este sistema é um sistema possı́vel com múltiplas soluções. No caso especı́fico do jobshop a matriz AT tem posto cheio e temos um grau de liberdade gl = r0 − 2n0 . O único
cuidado a ser tomado é o de buscar uma solução em que as coordenadas de y sejam
Método de Pontos Interiores e o Seqüenciamento Job-Shop
65
positivas. Consideramos as variáveis livres com um valor fixo e avaliamos a influência
deste valor no progresso do algoritmo.
Na análise seguinte, tomamos o ponto t0 = (2, 10, 3) e avaliamos após vinte
iterações o resultado variando primeiro o parâmetro θ e depois fixamos o melhor valor
deste parâmetro e variamos o valor das variáveis duais. O resultado é apresentado na
tabela 3.5.
Valor de θ
Função Objetivo
Ajute das variáveis duais
Função Objetivo
1
13,12
1
13,61
2
13,58
2
12,89
3
12,89
3
12,90
4
12,10
4
13,26
5
12,13
5
13,35
Tabela 3.5: Análise dos parâmetros para definição das variáveis de excesso e variáveis duais
Os valores usados para análise foram baixos devido ao tamanho do espaço de
busca ser bem restrito. Percebe-se uma maior sensibilidade na escolha das variáveis
duais. O parâmetro θ assumindo valor nulo não oferece resultados por permitir que
alguma coordenada do vetor s seja nula. Desta fora obtemos as variáveis de excesso e
duais dadas por:










s= 










10
5
7
15
8
18
10
17

2





 0, 083





 4





 2
 y= 



 2





 2





 2


2




















Para iniciar o algoritmo, ainda será preciso definir o valor dos parâmetros µ,
epsilon e β iniciais. Para isso, primeiro calcularemos o valor de ν(z 0 ) que oferece uma
medida da distância entre a aproximação corrente e um provável ponto de KKT para
o problema 3.5. Definiremos então valor de µ em função desta distância, como:
µ = δν(z 0 ) onde 0 < δ < 1
Em seguida calcularemos o valor de νµ (z 0 ) e definimos β e ²
Método de Pontos Interiores e o Seqüenciamento Job-Shop
β ≥ 2µr0
66
² = min{νm u(z 0 ), β1 }
Neste exemplo que estamos considerando os valores obtidos tendo como ponto
inicial t0 = (2, 10, 3) foram:
µ = 14 ² = 0.004463 β = 224
A razão para essa definição destes parâmetros β, ² e µ será vista de forma
mais clara na seção 3.3 onde analisaremos a convergência do método.
3.2.3.2
Encontrando as direções de busca
Procuraremos as direções de busca (4t, 4s) resolvendo o sistema (3.15). Fa-
zemos isto logo após o ajuste feito para garantir que a matriz Nβ seja definida positiva.
Isto é feito da forma apresentada na seção 3.2.2. Garantindo a positividade de Nβ ,
pelo teorema 3.3 vimos que podemos garantir a positividade da matriz dos coeficientes M para o sistema 3.15. Sendo assim, usaremos a decomposição de Cholesky da
matriz M para obter a sua inversa e conseqüentemente as direções primais (4t, 4s).
Descobrimos em seguida a direção dual fazendo uso da expressão 4y = γ − S −1 Y 4s
apresentada pelo teorema 2.25. Com este procedimento encontramos as direções de
busca para uma nova aproximação de Newton e garantimos o decrescimento da função
de mérito Lβ,µ (t, s, y) na direção primal, conforme mostraremos de forma ilustrativa
com o exemplo usado nesta seção. Sobretudo nosso principal objetivo centra-se na
demonstração matemática, que será realizada na seção 3.3.
3.2.3.3
Definindo o tamanho de passo
Após o cálculo das direções de busca para o sistema de Newton 3.9 um algo-
ritmo de MPI normalmente calcula um próximo passo (t, s, y) → (e
t, se, ye) fazendo:
e
t = t + αp 4t
se = s + αp 4s
ye = y + αd 4y
Método de Pontos Interiores e o Seqüenciamento Job-Shop
67
Onde αp e αd representam o tamanho de passo primal e dual. Em nosso caso estaremos
definindo os passos primal e dual de forma que possamos garantir que as variáveis de
excesso e duais se mantenham estritamente positivas, bem como, as variáveis originais
do problema 3.5 sejam limitadas inferiormente. Assim estabeleceremos um tamanho
máximo de passo como:
p
αmax
¸
·
tr +κ
sr
= min 1; −κ 4sr : 4sr < 0; −κ 4tr : 4tr < 0
d
αmax
·
¸
yr
= min 1; −κ 4yr : 4yr < 0
onde 0 < κ < 1.
Como vimos na seção 3.1 o problema de seqüenciamento job-shop possui um
espaço de busca não convexo além de não apresentar qualquer garantia de mı́nimo local
ou global para pontos satisfazendo a condição de otimalidade de primeira ordem, que é o
objeto de busca no método de pontos interiores. Diante destas questões aqui reforçadas,
mostraremos que as direções primais (4t, 4s) são direções de decrescimento para a
função de mérito Lβ,µ (t, s, y) e conseqüentemente permitem similar decrescimento para
a função objetivo do problema original. Desta forma, estaremos buscando uma forma
de garantir o decrescimento de Lβ,µ (t, s, y).
p
d
Inicialmente selecionamos αp = αmax
e αd = αmax
e descobrimos o próximo
candidato primal-dual e
t = t + αp 4t; se = s + αp 4s; ye = y + αd 4y. Se ze = (e
t, se, ye)
não reduzir o valor da função de mérito ν(z) de um fator 0 < q < 1 então esta
aproximação ze falha. Neste caso, mantemos a aproximação dual y e usamos a direção
primal 4p = (4t, 4s) para descobrir uma nova aproximação. Mostraremos na seção
3.3 que a direção primal 4p = (4t, 4s) é uma direção de decrescimento para a função
p
] um valor de αp
de mérito Lβ,µ (t, s, y). Sendo assim, buscaremos no intervalo [0, αmax
que atenda a condição de Armijo apresentada em anexo (A.3), ou seja, buscaremos αp
de forma que:
Lβ,µ (p + αp 4p, y) − Lβ,µ (p, y) ≤ ηαp < ∇Lβ,µ (p, y), 4p >;
onde 0 < η < 1
Assim que o algoritmo descobrir um valor mı́nimo irrestrito pe para Lβ,µ (p, y)
Método de Pontos Interiores e o Seqüenciamento Job-Shop
68
então buscará uma melhor aproximação para a variável dual através da fórmula
ye = y + βρ(e
t, se)
Como mencionado, faremos do exemplo aqui utilizado apenas para ilustrar
os objetivos da demonstração que se seguirá. Tomamos para tal o ponto inicial t0 =
(2, 10, 3) já mencionado e seus respectivos valores de µ, ² e β. Os resultados são
apresentados na tabela 3.6
Iteração
Variáveis Primais
Valor Objetivo
νz
Lβ,µ
1
( 2.0000049, 10.024731, 1.574525)
13.599261
71.826185
198850.8
2
( 2.0000293, 10.074941, 0.8261506)
12.901121
32.932195
99833.644
3
( 2.0000307, 10.083898, 0.4332541)
12.517183
27.997772
46523.234
4
( 2.0000336 , 10.09359 , 0.2269834)
12.320607
28.000595
29707.627
5
( 2.0000362, 10.100711, 0.1186913)
12.219439
28.00354
23642.025
6
( 2.0000367, 10.102784, 0.0618379)
12.164659
27.998493
21328.024
7
( 2.0000377, 10.10527, 0.0319899)
12.137298
28.006775
20541.837
8
( 2.0000383, 10.106532, 0.0163197)
12.12289
28.005997
20174.126
9
( 2.0000384, 10.106951, 0.0080928)
12.115083
28.000285
20004.335
10
( 2.0000385, 10.10724, 0.0037737)
12.111052
28.003013
19928.984
20
(2.0000386, 10.107604, - 0.0009905)
12.106652
28.001953
19850.207
Tabela 3.6: Exemplo de Aplicação do MPI ao problema de Job-Shop
Uma outra observação que é pertinente ao caso do job-shop é o ajuste da
Hessiana do Lagrangeano caso a matriz normal Nβ não seja definida positiva. No
exemplo ora apresentado, foi preciso a partir da segunda iteração e o valor deste ajuste
variou de λ = 0, 165418 até λ = 0, 021952 nas últimas iterações. Caso não fosse
realizado tal ajuste, não só deixa de haver a redução do valor objetivo, até chegar o
ponto de não haver solução para busca de novas direções.
Finalmente, queremos através deste exemplo ilustrar os objetivos das demonstrações que se seguirão na seção 3.3. Mostraremos que a direção primal é uma direção
de decrescimento para o Lagrangeano aumentado do problema em questão com a conseqüente redução da função objetivo. Demonstraremos também, que a solução convergirá para um provável ponto de otimalidade de primeira ordem para o problema
original.
Uma proposta sugestiva para o algoritmo do Método de Pontos Interiores em
questão pode ser visto no anexo B.2.
Análise de Convergência
3.3
69
Análise de Convergência
Nesta seção faremos uma análise de convergência para o método proposto na
seção 3.2.3 ao ser aplicado a um problema de seqüenciamento job-shop. Por ser um
problema não convexo com as caracterı́sticas apresentadas na seção 3.1, não poderemos
garantir uma convergência para um valor mı́nimo global. Estaremos buscando, entretanto, garantias de estarmos trilhando por um caminho de busca decrescente para a
função de mérito Lβ,µ (t, s, y) e que, se possı́vel, convirja para pontos de otimalidade de
primeira ordem para o problema 3.5. Estaremos nesta análise nos guiando por estudo
semelhante feito por Griva, et al [28] para caso convexo.
3.3.1
Condições para a convergência global do problema de
job-shop
A fim de auxiliar na análise de convergência a ser realizada nas seções poste-
riores verificaremos algumas caracterı́sticas do modelo matemático de seqüenciamento
job-shop que estamos adotando.
(C1) A função objetivo é limitada inferiormente por: f (t) ≥ f , ∀t ∈ Ω ⊂ Rn0 .
A função objetivo f (t) é uma função linear e não possui limite inferior para todo
t ∈ Rn0 , entretanto como estamos tratando com variáveis não negativas (t ≥ 0)
podemos considerar f ≥ −∞ como sendo um limite inferior para f (t). Note
que cuidados adicionais são tomados ao definir o tamanho de passo para uma
próxima iteração a fim de manter t limitado inferiormente.
(C2) O modelo atende a condição de Slater, ou seja, existe t ∈ Rn0 tal que gr (t) >
0, r = 1, ..., r0 . Esta condição é fácil de ser verificada bastando para isto tomar
um seqüenciamento onde todas as operações do produto Pi são realizadas antes
que as operações do produto Pi+1 aconteçam, para i = 1, ..., p. Apesar desta não
ser, provavelmente, a melhor solução ela é uma solução factı́vel em que se tem
gr (t) > 0. Assim, temos pontos que atendem a condição de Slater.
Análise de Convergência
70
(C3) As restrições gr (t) satisfazem as seguintes condições:
lim
min gr (t) = −∞
||t||→∞ 1≤r≤r0
Como vimos na seção 3.1 as restrições são todas lineares com exceção das restrições referentes às disjunções. De qualquer forma o terceiro e quarto grupo de
equações da função g(t) oferecem um limite inferior para gr (t) quando ||t|| → ∞.
(C4) O conjunto de restrições é formado por funções polinomiais em Rn0 sendo na sua
maioria funções lineares exceto o conjunto das restrições disjuntivas. Desta forma
podemos ver que a diferença do valor assumido pela função restritiva de maior e
menor valor é finita. Desta forma, conforme observação feita por Vanderbei [28]
assumimos que:
s µ¯
¯
¶
¯
¯
¯
¯
ln ¯ max gr (t)¯ + 1 ≤ − min gr (t) + C,
1≤r≤r0
1≤r≤r0
∀t ∈ Rn0
onde 0 < C < ∞ e depende do problema especı́fico em questão. Esta condição
possui certa relevância no estudo teórico que estamos realizando.
(C5) As Hessianas ∇2 f (t) e ∇2 gr (t), r = 1, ..., r0 satisfazem as condições de Lipschitz
em Rn0 .
Observação 3.2. Conforme visto na seção 3.1 não podemos garantir que o ponto de
mı́nimo do problema 3.1 satisfaça as condições de otimalidade de segunda ordem.
3.3.2
Prova de Convergência
Apresentaremos inicialmente alguns lemas necessários ao teorema principal que
oferece condições para convergência de nosso problema de seqüenciamento job-shop.
Lema 3.1. Assumindo as condições (C1) a (C4) existe pelo menos uma solução global
para o problema 3.6 para algum µ > 0.
Prova:
Análise de Convergência
71
Reescrevamos o problema 3.6 como
min B(t, µ) = f (t) − µ
r0
X
ln gi (t)
i=1
t ∈ Rn0
No caso do job-shop estamos trabalhando com um conjunto factı́vel Ω limitado
já que estabelecemos limites inferiores e superiores para todas as variáveis primais (ti ).
Tomemos um ponto estritamente interior, ou seja, um ponto t que atenda a condição
(C2). Tomemos, também, um valor constante Mµ = 2B(t, µ). Verificaremos que o
conjunto Ωµ = {t ∈ Ω : B(t, µ) ≤ Mµ } é compacto.
Primeiro note que Ωµ é um conjunto limitado pois é subconjunto de Ω que
vimos ser limitado. Também temos que Ωµ é fechado, pois se trata da imagem inversa
de um conjunto fechado por uma função contı́nua (B(t, µ)). Assim, concluı́mos que Ωµ
é compacto.
Como B(t, µ) é contı́nua, então pelo Lema de Weierstrass, existe um mı́nimo
global tµ tal que B(t, µ) ≥ B(tµ , µ) no conjunto Ωµ e conseqüentemente no conjunto
Ω.
¤
Como temos a garantia da existência de uma solução ótima global para o
problema (3.6) então poderemos buscar uma solução para o nosso problema original
(3.5), reduzindo o parâmetro µ tal que µ → 0. No entanto, estaremos utilizando o
Lagrangeano aumentado para guiar nossa busca pela solução global. Como mencionado na seção 3.2, é preciso garantir que o Lagrangeano aumentado do problema 3.6
(Lβ,µ (t, s, y)) seja limitado inferiormente, assim teremos um ponto de sela na solução
ótima. Esta análise é feita no lema a seguir.
Lema 3.2. Para algum y ∈ Rr0 , β ≥ 2r0 µ e µ > 0, existe um mı́nimo global
Mβ,µ (y) =
Prova:
min
r
t∈Rn0 ,s∈R+0
Lβ,µ (t, s, y) > −∞
Análise de Convergência
72
r0
r0
Sejam s ∈ R+
e t ∈ R+
fixos, sendo este último garantido pela condição (C2).
Tome M = 2Lβ,µ (t, s, y). Assim, como a função Lβ,µ (t, s, y) é contı́nua, para a prova
deste teorema basta mostrar que o conjunto
n0
: Lβ,µ (t, s, y) ≤ M }
zβ = {(t, s) ∈ Rn0 × R+
é um conjunto limitado e fechado como foi feito no teorema 3.1.
É fácil ver que zβ é fechado, pois se trata da imagem inversa de um conjunto
fechado por uma função contı́nua. Vamos agora verificar que zβ é limitado.
Suponha por contradição que zβ é ilimitado. Desta forma, existe uma seqüência
ilimitada {pl } = {(tl , sl )} definida em Rn0 × Rr0 tal que
(i)
t0 = t, s0 = s,
(ii)
liml→∞ ||pl − p0 || = ∞
(iii) liml→∞ Lβ,µ (tl , sl , y) ≤ M
Verificaremos que uma seqüência que satisfaz as condições (i) e (ii) terá
lim Lβ,µ (tl , sl , y) = ∞
(3.19)
l→∞
o que contradiz (iii).
Tomemos uma seqüência {pl } = {(tl , sl )} que satisfaça (i) e (ii). Usaremos
também as seqüencias {ρli } = {sli −gi (tl )} e {φli } = { β2 (ρli )2 +yi ρli −µ ln(gi (xl )+ρli )}, i =
1, ..., r0 . Supondo f (t) sendo limitada inferiormente, podemos provar (3.19) apenas
mostrando que
lim
l→∞
r0
X
φli = ∞
(3.20)
i=1
.
Dividiremos a prova em dois casos. Primeiro consideraremos que seqüencia {tl }
correspondente a {pl } é limitada. Neste caso a seqüencia {sl } é ilimitada. Neste caso
podemos assumir que existe um conjunto não vazio de indices I ∗ para as restrições de
forma que para cada ı́ndice i ∈ I ∗ tenhamos liml→∞ sli = ∞. Como a seqüencia {gi (tl )}
é limitada para qualquer ı́ndice i = 1, ..., m então temos que liml→∞ ρi (tl , sl ) = ∞ para
i ∈ I ∗ , e então:
β
lim φli = lim ( (ρli )2 + yi ρli − µ ln(gi (xl ) + ρli )) = ∞,
l→∞ 2
l→∞
i ∈ I∗
Análise de Convergência
73
logo, podemos garantir que (3.19) é verdade.
Vamos agora considerar o caso em que a seqüencia {tl } correspondente a {pl }
seja ilimitada. Neste caso vamos estimar o valor de φli primeiramente para gi (tl ) ≤ 1,
então
φli =
β l 2
β
(ρi ) + yi ρli − µ ln(gi (tl ) + ρli ) ≥ (ρli )2 + yi ρli − µ ln(1 + ρli ) ≥ −B1
2
2
(3.21)
para algum B1 ≥ 0 suficientemente grande.
Se gi (tl ) ≥ 1, relembrando que sli = gi (tl ) + ρli > 0, nós temos:
φli = β2 (ρli )2 + yi ρli − µ ln(gi (tl ) + ρli )
= β2 (ρli )2 + yi ρli − µ ln gi (tl ) − µ ln(1 +
ρli
)
gi (tl )
ρl
≥ β2 (ρli )2 + yi ρli − µ ln gi (tl ) − µ − µ gi (ti l ) )
≥ β2 |ρli |2 − |yi ||ρli | − µ ln gi (tl ) − µ − µ|ρli |
≥ −µ ln gi (tl ) − B2
onde B2 é grande o bastante. Relembrando da condição (C4) analisada em relação ao
modelo de job-shop adotado, nós obtemos
µ
¶
l
l
−µ ln gi (t ) − B2 ≥ −µ ln max gi (t ) − B2
¯
µ¯
¶1≤i≤r0
¯
¯
≥ −µ ln ¯¯ max gi (tl )¯¯ + 1 − B2 ≥ −µ(C − min gi (tl ))2 − B2
1≤i≤r0
1≤i≤r0

 −µC 2 − B ,
se gi0 (tl ) ≥ 0
2
= −µ(C − gi0 (tl ))2 − B2 ≥
 −µ(C + ρl − B , se g (tl ) ≤ 0
i0
2
i0
≥ −µ max{c2 , (C + ρi0 )2 } − B2
onde i0 é o ı́ndice da restrição tal que gi0 = min gi (tl ). Como lim
1≤i≤r0
min gi (t) =
||t||→∞ 1≥i≥r0
−∞ e a seqüencia {tl } é ilimitada, temos:
lim ρi0 (t) = +∞
||t||→∞
Então para toda seqüencia com l suficientemente grande e, na pior das hipóteses,
supondo que gi0 (tl ) < 0 nós temos:
φli ≥ −µ(C + ρli0 )2 − B2
(3.22)
Análise de Convergência
74
Combinando as equações (3.22) e (3.21), nós obtemos para l suficientemente
grande:
Pr0
i=1
= φli0 +
P
i6=i0 :gi (tl )<1
φli +
P
i:gi (tl )≥1
φli
≥ β2 (ρli0 )2 + yi ρli0 − µ ln ρli0 − r0 B1 − (µ(C + ρli0 )2 + B2 )r0
Como estamos tomando β > 2µr0 isto garante que a condição (3.20) é verdadeira, logo
a equação (3.20) também o é. Desta forma encontramos uma contradição em relação
a condição (iii) postulada inicialmente.
Assim podemos concluir que zβ é compacto e Lβ,µ (tl , sl , y) possui um mı́nimo
global em Rn0 × Rr+0 .
¤
O lema seguinte apresenta condições necessárias para que a direção primal
4p = (4t, 4s), obtida como solução do sistema (3.13) seja uma direção de decrescimento para Lβ,µ (t, s, y).
Lema 3.3. Para algum β > 0, existe θ > 0 tal que para alguma aproximação primalr0
dual (t, s, y) com s, y ∈ R+
, a direção primal 4p = (4t, 4s), obtidas como solução
do sistema (3.13) com o ajuste feito na matriz N² (t, s, y) dado pela equação (3.16) e
tendo como parâmetro ² = β1 , é uma direção de descida para Lβ,µ (t, s, y) e
(∇p Lβ,µ (t, s, y), 4p) ≤ −θ||4p||2
Prova:
1
, como mencionado na
β
seção 3.2.2, na demonstração do teorema 2.4 vimos que o sistema (3.13) pode ser
Assumindo o parâmetro de regularização dual ² =
reescrito em função das direções primais como:



 

−σ + βA(t)T ρ
4t
H(t, y) + βAT A −βA(t)T

 = 
 

−1
−1
S γ − βρ
4s
−βA(t)
S Y + βI
Por outro lado o gradiente de Lβ,µ (t, s, y) com respeito a t e s é dado por:
∇t Lβ,µ (t, s, y) = σ − βAT ρ
∇s Lβ,µ (t, s, y) = −S −1 γ + βρ
Análise de Convergência
75
Portanto, assumindo que a matriz Nβ = H +AT [β −1 I +Y −1 S]−1 A seja positiva
definida conforme ajuste realizado pela equação (3.16), nós temos então pelo teorema
3.3 que


T 
∇t Lβ,µ (t, s, y)
∇s Lβ,µ (t, s, y)




4t
4s
 = −

T 
4t
 
T
H + βA A
−βA
4s
−βA
S
−1
T
Y + βI


4t

4s
≤ −α max{||4t||, ||4s||}2
onde α depende dos parâmetros λN e β que são respectivamente os menores autovalores
de Nβ e de [S −1 Y + βI] respectivamente.
¤
Lema 3.4. Considere as séries
{sk }, onde
∞
X
ai que é uma seqüência das maiores somas parciais
i=0
sk = sup
l
X
0≤l≤k i=1
ai
é ilimitada, monótona e crescente, isto é
lim sk = +∞
k→∞
Também considere a seqüência {bk } com bk ≥ 1 sendo monótona crescente e tal que
∞
X
lim bk = +∞. Então para a série
ai bi da seqüência das maiores somas parciais de
k→∞
{pk }, onde
i=0
pk = sup
l
X
0≤l≤k i=1
ai bi
é também monótona e crescente, ou seja,
lim pk = +∞
k→∞
Este lema será usado na demonstração do 3.4 e sua prova pode ser encontrada
no anexo do artigo de Griva et al [28].
Teorema 3.4. Dentro das condições (C1)-(C5) assumidas para este modelo matemático
do problema de seqüenciamento job-shop, o algoritmo de pontos interiores gera uma
Análise de Convergência
76
seqüencia primal-dual {z u = (tu , su , y u )} tal que algum ponto limite t da seqüencia primal {tu } é ponto de otimalidade de primeira ordem para a minimização da norma do
vetor de violação das restrições v(t) = (v1 (t), ..., vr0 (t)) onde vi (t) = min{gi (t), 0}:
V (t) = ||v(t)||
Se em particular, V (t) = 0 então t = t∗ é um ponto de otimalidade de primeira ordem
para o problema 3.5.
Prova:
Tomemos z ∗ = (t∗ , s∗ , y ∗ ) sendo um ponto de mı́nimo local ou global para o
problema (3.5) e tomemos a seqüência {z l }, onde z l = (tl , sl , y l ) = (pl , y l ), sendo gerada
pelo algoritmo a partir de uma aproximação inicial z 0 .
O modelo estudado não apresenta garantias de alcançar um ponto de mı́nimo
local ou global. Como vimos trata-se de um problema não convexo e, em particular,
tendo a Hessiana do Lagrangeano sendo definida negativa em todo o espaço de busca.
Sendo assim, o algoritmo proposto minimiza a função de mérito Lβ,µ (t, s, y) em p =
(t, s). Vimos pelos lemas 3.2 e 3.3 associados à regra de Armijo (A.3) que para um
valor fixo dos multiplicadores de Lagrange y e uma escolha adequada do parâmetro β
a direção primal 4p = (4t, 4s) satisfaz a seguinte condição:
(∇p Lβ,µ (p, y), 4p) ≤ −α||4p||2
Portanto, o algoritmo pode eventualmente decrescer até uma aproximação pe que um
ponto de otimalidade de primeira ordem para a minimização irrestrita de Lβ,µ (t, s, y).
Após encontrar esta aproximação o algoritmo muda os multiplicadores de Lagrange
por esta fórmula
y l+1 := y l + βρ(e
t, se)
(3.23)
se esta mudança reduzir a função de mérito νµ (z) por um fator 0 < q < 1. De outra
forma, o algoritmo incrementa o valor do parâmetro de penalidade β e continua a
minimização de Lβ,µ (t, s, y) em p = (t, s).
Nosso objetivo é verificar se algum ponto limite da seqüência gerada pelo
algoritmo é um ponto de otimalidade de primeira ordem para o problema (3.5), ou
Análise de Convergência
77
seja:
lim ν(z l ) = 0,
l→∞
lim sl ≥ 0,
l→∞
lim y l ≥ 0.
l→∞
Temos dois possı́veis cenário para análise. O primeiro ocorre quando a minimização da função de mérito Lβ,µ (p, y l ) em p para valores grandes de β é seguida da
alteração dos multiplicadores de Lagrange. Isso ocasiona uma trajetória próxima da
solução do problema com barreira (3.6) devido às propriedades de convergência global
do algoritmo do Lagrangeano aumentado [8, 34]. Nesse caso o algoritmo reduz o valor da função de mérito νµ (z). Portanto, o valor da função de mérito ν(z) pode ser
estimado por
ν(e
z ) ≤ νµ (e
z ) + µ = νµ (e
z ) + δτ
Onde τ é o valor da função de mérito ν(z) da iteração anterior e 0 < δ < 1. Portanto,
a redução da função de mérito νµ (z) garante a redução de ν(z).
O segundo cenário acontece quando o algoritmo não muda os multiplicadores
de Lagrange y pela fórmula (3.23) já que tal mudança não reduziria o valor da função
de mérito νµ (z). Portanto o algoritmo transforma-se numa seqüência de minimização
irrestrita do Lagrangeano aumentado Lβ,µ (t, s, y) na direção primal p, seguido pelo
incremento sucessivo do parâmetro de penalidade β. Mostraremos então que algum
ponto limite desta seqüência primal {tl } é na verdade um ponto de otimalidade para
minimização da norma do vetor de violação de restrições v(t) = (v1 (t), ..., vr0 (t)) onde
vi (t) = min{gi (t), 0}:
V (t) = ||v(t)||
Primeiro mostraremos que a seqüência primal {tl } é limitada. Considere a
seqüência monótona crescente 2ro µ ≤ β 0 ≤ β 1 ≤ ... ≤ β k ≤ .... Reescrevamos a função
Análise de Convergência
78
de mérito Lβ,µ (p, y) como
β T
ρ ρ
2·
µ
¶
¸
0
β
−
β
1
β
= (1 + β − β 0 )
Lµ (p, y) + ρT ρ +
ρT ρ
1 + β − β0
2
2(1 + β − β 0 )
1
= [ξh1 (p, y) + (1 − ξ)h2 (p, y)]
ξ
1
= θξ (p, y)
ξ
Lβ,µ (p, y) = Lµ (p, y) +
Onde:
1
1 + β − β0
r0
X
Lµ (p, y) = f (t) − µ
ln si + y T ρ,
ξ =
i=1
h1 (p, y) = Lµ (p, y) + 0, 5βρT ρ,
h2 (p, y) = 0, 5ρT ρ
θξ (p, y) = σh1 (p, y) + (1 − ξ)h2 (p, y)
Portanto, a seqüência de minimização irrestrita da função de mérito Lβ l ,µ (p, y) em p
para a seqüência não decrescente 2ro µ ≤ β 0 ≤ β 1 ≤ ... ≤ β k ≤ ... é equivalente a
minimização irrestrita da função θξ (p, y) em p para a seqüência não crescente 1 = ξ 0 ≥
ξ 1 ≥ ... ≥ ξ k > 0.
Suponha por absurdo que a seqüência primal {pl } seja ilimitada. Relembrando
que
lim
min gi (t) = −∞
||t||→∞ 1≤i≤m
pela condição (C3) e como {pl } é ilimitada, então a seqüência {hl2 }, onde hl2 = h2 (pl , y)
é ilimitada e
lim sup hl2 = +∞
k→∞ 0≤l≤k
(3.24)
Vamos renomear a seqüência {pl } como:
p0 = pq0 , pq0 +1 , ..., pq0 +d0 = pq1 , pq1 +1 , ..., pq1 +d1 = ... = pqk , pqk +1 , ..., pqk +dk , ...
Para todo pl , l = qk , ..., qk + dk corresponde ao mesmo valor de ξ k . Para algum k, e
para todo l = qk , ..., qk + dk − 1 nós temos
ξ k hl+1
+ (1 − ξ k )hl+1
≤ ξ k hl1 + (1 − ξ k )hl2
1
2
Análise de Convergência
79
, logo:
hl1
−
hl+1
1
1 − ξ k l+1
≥
(h2 − hl2 )
k
ξ
(3.25)
Substituindo na equação (3.25) todo l = qk , ..., qk + dk − 1 nós obtemos:
hq1k − hq1k +dk ≥
1 − ξ k qk +dk
(h2
− hq2k )
ξk
(3.26)
Após a soma da inequação (3.26) para todo k = 0, 1, ..., j e tendo em mente
q
q
que hq1k +dk = h1k+1 e hq2k +dk = h2k+1 para k = 0, 1, 2..., j − 1, nós obtemos
h01
−
q +d
h1j j
≥
j
X
1 − ξk
ξk
i=1
(hq2i +di − hq2i )
(3.27)
Assumindo que l = qj + dj relembramos que
lim sup
k→∞ 0≤l≤k
hl2
= lim sup
k→∞ 0≤l≤k
j
X
(hq2i +di − hq2i ) = +∞
i=1
Como a seqüência {ξ k } é monotonicamene decrescente para zero, a seqüência
k
1−ξ
} é monótona, crescente e ilimitada. Portanto, pelo lema 3.4 do anexo nós
ξk
temos:
j
X
1 − ξ i qi +di
− hq2i ) = +∞
(h2
lim sup
i
k→∞ 0≤l≤k
ξ
i=1
{
Utilizando (3.27) obtemos:
lim sup (h01 − hl1 ) = +∞
k→∞ 0≤l≤k
ou seja,
lim inf hl1 = −∞
k→∞ 0≤l≤k
que contradiz o lema 3.2. Portanto, podemos concluir que a seqüência primal {pl }
gerada pelo algoritmo é limitada.
Agora falta mostrar que qualquer ponto limite da seqüência primal {tl } gerada pelo algoritmo é na verdade um ponto de otimalidade de primeira ordem para
minimização da norma do vetor de violação de restrição v(t) = (v1 (t), ..., vr0 (t)) onde
vi (t) = min{gi (t), 0}:
V (t) = ||v(t)||
Análise de Convergência
80
Uma condição necessária para o par primal pe = (e
t, se) minimizar a função de mérito
Lβ,µ (p, y) em p é o seguinte sistema
∇f (t) − A(t)T (y + βρ) = 0
−µS −1 e + y + βρ = 0
(3.28)
Se ze = (e
t, se, ye), onde ye = y + βρ satisfaz o sistema (3.28) então a única razão para que
a função de mérito νµ (e
z ) não seja nula é a infactibilidade, ou seja, ρ(e
t, se) 6= 0.
Consideremos a seqüência {z l }, z l = (tl , sl , y l ) gerada pelo algoritmo. A
seqüência {y l } já não muda mais, então assumimos que y l = y para l ≥ l0 .
De acordo com o algoritmo para a seqüência de aproximações primais na busca
de um valor mı́nimo para a função de penalidade Lβ,µ (t, s, y), nós temos:
∇f (tk ) − A(tk )T (y + β k ρ(tk , sk )) = Υkn0
−µSk−1 e + y + β k ρ(tk , sk ) = Υkr0
(3.29)
onde lim Υkn0 = 0 e lim Υkr0 = 0.
k→∞
k→∞
Se a seqüência primal {tk , sk } satisfaz o sistema (3.30) então satisfará o seguinte sistema:
Υkn0
∇f (tk ) A(tk )T y
k
k k
−
+ A(t )ρ(t , s )) =
βk
βk
βk
k k
k
S Υr0
−µ + S y
+ S k ρ(tk , sk ) =
k
β
βk
(3.30)
Como a seqüência {(tk , sk )} é limitada, nós temos:
lim A(tk )ρ(tk , sk ) = 0,
k→∞
lim (ski − gi (tk ))ski = 0, i = 1, ..., r0
k→∞
(3.31)
lim ski ≥ 0, i = 1, ..., r0
k→∞
Observe que as condições (3.31) são na verdade as condições de otimalidade de primeira
ordem para o problema
min ||s − gi (t)||2 ,
s.a. s ≥ 0.
Por sua vez a solução (t∗ , s∗ ) do problema (3.32) minimiza V (t)
(3.32)
Conclusão
81
¤
Note que a garantia oferecida por este teorema é de que há convergência para
pontos que minimizem a violação das restrições originais do problema 3.5 à medida que
minimiza a função objetivo deste mesmo problema, ao minimizar a função de mérito
Lβ,µ (t, s, y).
Conclusão
Um problema de seqüenciamento job-shop certamente constitui um desafio
como problema de programação matemática. Pela análise do modelo contı́nuo adotado,
percebe-se a dificuldade a ser enfrentada primeiro por se tratar de um problema não
convexo e, além disto, por não podermos garantir a minimalidade nem mesmo local
para pontos de otimalidade de primeira ordem. Como o método de pontos interiores faz
uma busca por pontos de otimalidade de primeira ordem para o problema em questão,
foi preciso guiar esta busca a fim de garantir o decrescimento da função objetivo. Para
tanto, utilizamos o Lagrangeano aumentado que foi decrescido à medida que buscamos
pontos estacionários.
Dentre as várias mudanças que se fizeram necessárias, destacamos aquela feita
na matriz Hessiana do Lagrangeano. Apresentamos o impacto que esta mudança poderia trazer na convergência do problema dual e adotamos então um processo de regularização da variável dual além de maior cuidado na variação desta variável. Apesar de
não podermos garantir a convergência global o resultado é significativo já que estabelece um direção de busca decrescente para a função objetivo respeitando as restrições
originais do problema. Isto é relevante tendo em vista a dificuldade de resolução do
problema de job-shop.
Pelas caracterı́sticas detalhadas em relação a modelagem contı́nua adotada,
é possı́vel perceber a relevância de se tomar cuidados especiais para resolução deste
modelo.
Conclusão Geral
Inicialmente, verificamos através da descrição do problema de job-shop, caminhos diferentes para se tratar esse problema. A modelagem contı́nua permitiu uma
abordagem matemática direta do aspecto combinatório desse problema. Pelo estudo
desse modelo foi possı́vel visualizar a dimensão da dificuldade imposta na resolução de
problemas de seqüenciamento job-shop. Por se tratar de um problema de programação
não conexo, não conseguimos garantias de obtermos um ponto de mı́nimo global para o
problema em questão. Contudo, obtemos uma direção de decrescimento para a função
objetivo à medida que buscamos pontos de otimalidade de primeira ordem.
Mostramos, também, que as mudanças feitas no método de pontos interiores
permitiu encontrar essas direções primais decrescentes para o Lagrangeano aumentado
que foi utilizado como função de mérito guiando o algoritmo por direções que permitem a redução da função objetivo escolhida para o seqüenciamento. Devido a estrutura
particular do job-shop foi possı́vel um ajuste relativamente fácil da Hessiana do Lagrangeano. O adequado ajuste da Hessiana tornando a matriz normal Nβ definida positiva
é fundamental para o decrescimento da função objetivo ao longo das iterações. Uma
pequena amostra disto pode ser visto no problema-exemplo 2 visto anteriormente. Em
casos gerais, ajuste similar pode ser feito conforme proposto por Griva et al [28]. Neste
sentido, a associação do método de pontos interiores com as técnicas de otimização
envolvendo o Lagrangeano aumentado, como foi feito nesse caso, pode ser estendido a
outros caso de programação não convexa.
O principal objetivo deste trabalho, foi realizar uma análise matemática fundamentando a utilização do método de pontos interiores na resolução de um problema
de seqüenciamento job-shop. Desta forma, consideramos como principal contribuição o
Conclusão Geral
83
fato de poder apresentar resultados teóricos que apontam numa direção positiva para
prática em casos combinatórios como este. Não foi nossa proposta uma implementação
computacional adequada, mas diante do que apresentamos, tal tarefa pode ser realizada devidamente fundamentada em bases matemáticas. Também deixamos claro as
dificuldades inerentes ao próprio problema que permanecem como um desafio para a
efetiva solução deste. Uma idéia disto é possı́vel sentir através da resolução de um
pequeno exemplo como foi o nosso caso.
Acreditamos acima de tudo, que as análises aqui realizadas servem de ponto de
partida para várias outras pesquisas futuras envolvendo o método de pontos interiores
como alternativa para problemas de seqüenciamento job-shop. Assim, consideramos
como a principal motivação para um trabalho futuro, a busca de uma implementação
computacional mais adequada da metodologia aqui apresentada. Para efetivação deste
intento, será preciso testes práticos a fim de adequar os parâmetros a casos gerais.
Dentre outras coisas, destacamos como um dos ı́tens a ser analisado, o estudo de
formas efetivas para obtenção de um ponto de partida interior adequado. Como visto na
seção 3.2.3 pontos factı́veis distintos podem apresentar resultados diferentes. Em nossa
análise do ponto de partida consideramos inicialmente as sugestões apresentadas tanto
por Wright [57] como por Vanderbei e Shanno [56]. Entretanto, pela breve experiência
no caso prático percebemos a necessidade de mudança, que foi feito no ajuste da variável
de excesso. Esta escolha adequada das variáveis de excesso e variáveis duais é realçada
no exemplo ora citado. Neste caso particular, como o espaço de busca é muito pequeno
a convergência logo se torna lenta por se aproximar das extremidades da região factı́vel
e isto precisa ser estudado de forma mais ampla para casos de maior dimensão. Vemos
também, que seria útil agregar heurı́sticas adaptativas como algoritmo genético para
esta auxiliar na melhor seleção do ponto inicial.
Gostarı́amos ainda de destacar duas outras possibilidades para estudo. Primeiramente, em virtude da grande complexidade computacional de problemas de job-shop,
vemos como promissora a associação desta metodologia com métodos de decomposição.
Nesse sentido, temos a proposta feita por Alves [3] que utiliza as técnicas de Relaxação
Lagrangeana para acoplar em um nı́vel coordenador os subproblemas obtidos pela decomposição feita através de técnicas da Tecnologia de Grupos. Nessa proposta, os
Conclusão Geral
84
subproblemas também constituem problemas de job-shop, mas de menor dimensão.
Dessa forma, a metodologia de pontos interiores poderia ser usada como ferramenta de
resolução desses subproblemas.
Por fim, uma outra abordagem a ser considerada seria a utilização de uma
modelagem linear para o problema de job-shop o que permitiria a utilização de outras
versões de método de pontos interiores que apresentam, nesse caso, uma convergência
super-linear (Wright [57], Mehrotra [39]). Entretanto, o aspecto combinatório, que
vimos como uma das caracterı́sticas mais desafiadoras desse problema, deveriam ser
tratadas por heurı́sticas como algoritmo genético e simulated annealing ou por métodos
de Branch-and-Bound.
Bibliografia
[1] Adams, J.; Balas, E. e Zawack, D. (1988) “The shifting bottleneck procedure
for job shop scheduling”. Management Science, 34, 391-401.
[2] Adler, I.;Karmarkar, N.; Resende, M.; Veiga, G.(1989) “An implementation of Karmarkar algorithm for linear programming”. Mathematical Programming 44,297-332.
[3] Alves, I. C. (2000)“Aplication de la Technologie de Groupes Et de la Relaxation Lagrangienne au Probleme D’Ordennancement de Type Job-Shop”. Tese de
Doutorado, Universitè Blaise Pascal.
[4] Akrotirianakis, I.; Rustem, B.(1997)“A Globally Convergent Interior Point
Algorithm for General Non-Linear Programming Problems”. Technical Report
97/14, Department of Computing, Imperial College of Science, Technology and
Medicine, London.
[5] Azevedo,
A.T.;
Soares,
S.;
Oliveira,
A.R.L.;
Carvalho,
M.F.H.(2002)“Métodos de Pontos Interiores Aplicados a Problemas de Multifluxo com Restrições Adicionais”. Tendências em Matemática Aplicada e
Computacional, 3, No. 1, 41-50.
[6] Baker, K.R. (1974), “Introduction to sequencing and scheduling”. John Wiley e
Sons, New York, USA.
[7] Barbosa, C.B. (2003)“Planejamento do Tratamento por Radioterapia Através
de Método de Pontos Interiores ”. Dissertação de Mestrado, USP - Instituto de
Ciências Matemáticas e de Computação .
Referências Bibliográficas
86
[8] Bazaraa, M.S.; Jarvis, J.J.; Sherali, H.F.(1990)“Linear Programming and
Network Flows”. John Wiley e Sons, New York, USA, 380-418.
[9] Benson, H.; Shanno, d.; Vanderbei, R.(2002)“Interior Point Methods for
Nonconvex Nonlinear Programming: Filter Methods and Merit Functions”. Computational Optimization and Applications, 23:257-272.
[10] Blazewicz, J.; et al.(1996)“Scheduling Computer Manufactoring Process”.
Springer-Vertag, Berlin.
[11] Blazewicz, J.(1987)“Selected Topics in Scheduling Theory”. Annals of Discrete
Mathematics, vol.31, 1-60.
[12] Carlier, J.; Pinson, E.(1987)“ A Branch and Bound Method for the Job-Shop
Problem”. Technical Report Institut de Mathémathiques Appliquées, Université
de Angers.
[13] Carlier, J.; Pinson, E.(1989)“ An Algorithm for Solving the Job- Shop Problem”. Management Science, vol. 35, No. 2, 164-176.
[14] Castro, J.(2003): “Un Algoritmo de Punto Interior para Flujos Multiartı́culo
Cuadráticos”. XXVII Congresso Nacional de Estadı́stica e investigacı́on Operativa,
Lleida,Itália.
[15] Castro, J.(2000): “A Specialized Interior-point Algoritm for Multicommodity
Network Flows”. SIAM J. on Optimization 10(3),852-877.
[16] Castronuovo, E.D.; Campagnolo, J.M.; Salgado, J.(2000)“A Largest-Step
Central-path Algorithm Applied to the Optimal Power Flow Problem”. SBA Controle e Automação vol. 11 no. 3, 176-181.
[17] El-Bakry, A.S.; Tapia, R.A.; Tsuchida, T.; Zhang, Y(1996)“On the Formulation and T Theory of the Newton Interior-Point Method for Nonlinear Programming”. Journal of Optimization Theory and Application, Vol. 89, No. 3, pp.
309-332.
[18] Fiacco, A.V.; McCormick, G.P.(1968),“ Nonlinear Programming: Sequential Unconstrainted Minimization Techniques”. Research Analysis Corporation,
McLean Virginia.
Referências Bibliográficas
87
[19] Fisher, M. L. (1973) “Optimal solution of scheduling problems using Lagrange
multipliers: parte I”, Oper. Res, Vol21,1114-1127.
[20] Fisher, M. L. (1973) “Optimal solution of scheduling problems using Lagrange
multipliers: parte II”, In: Syposum on the theory of scheduling and its Applications, Springer, Bertin, 294-318.
[21] Fisher, M.L.; Lageweg, B.J.; Lenstra, J.K.; Kan A.H.G.R. (1983) “Surrogate Duality Relaxation for job shop scheduling”, Discrete Applied Mathematics.
Vol.5,65-75.
[22] Freund, R.M.;Mizuno, S.;(1996),“Interior Point Methods: Current Status and
future directions”. Optima, 51,1-9.
[23] Fritzsche, Helmut(1978)“Programação Não-Linear: Análise e Métodos”. São
Paulo: Editora Edgard Blücher.
[24] Garcia, H. et Proth, J.M.(1985)“Group Technology in Production Management: The Short Horizon Planning Level”. Appl. Stoch. Meth. and Data
Analys.,vol. 1, No. 1, 25-34.
[25] Goldberg, D.E.(1989) “Genetic Algorithms in Search: Optimization and Machine Learning”. Addison-Wesley, Reading, MA.
[26] Gondzio, J.; Sarkissian, R. e Vial, J.P.(1995) “ Using an Interior Point
Method for the Master Problem in a Decomposition Approach”.European Journal
of Operation Reseach, 101, 577-587
[27] Granville, S.(1994) “Optimal Reactive Dispacht through Interior Point Method”.
IEEE Trans. on Power Systems, vol.9, no. 1, pp.136-146.
[28] Griva, I.; Shanno, D.F.; Vanderbei, R.J.(2004) “Convergence Analysis of a
Primal-Dual Interior-Point for Nonlinear Programming”. Technical Report, Princeton University, Department ORFE; Rutgers University, RUTCOR.
[29] Jain, A.S.; Meeran, S.(1998)“Deterministic Job-Shop Scheduling: Past, Present and Future”. European Journal of Operational Research, Vol. 113, pp. 390434.
Referências Bibliográficas
88
[30] Johnson, D.S.; Sethi, R. e Garey, M.R.(1976)“The Complexity of Flowshop
and Jobshop Scheduling”. Mathematics of oeration research, vol.1.
[31] Karmarkar, N.(1984) “A new polinomial-time algorithm for linear programming”. Combinatórica, Vol. 4, No 4, 373-395.
[32] Kranich, E.(1991)“Interior Point Methods for Mathematical Programming : A
Bibliographi”. Diskussionsbeittrag, 171, Germany.
[33] Kusiak A. (1989)“ Knowledge -based systems in manufacturing ”, Taylor & Francis, New York.
[34] Luenberger, D.G.(1984)“Linear and Nonlinear Programming”. Addison-Wesley
Publishing Company.
[35] Lenstra, J.K.; Rinooy Kan, A.H.G. (1977)”Complexity of machine scheduling
problem”. Annals of Discrete Mathematics, vol.1, pp.343-363.
[36] Mahey, P.(1987)“ Programação Não Linear: Uma Introdução à Teoria e aos
Principais Métodos”. Rio de Janeiro: Campus.
[37] Megiddo, N.(1987)“Pathways to the Optimal set in linear Programming”. Progress in Mathematical Programming: Interior Point and Related Methods Springer, New York, pp. 131-158.
[38] Mehrotra,S.(1992) “On the Implementation of a Primal-dual Interior Point
Method”. SIAM J. Optim. 2, 575-601.
[39] Mehrotra,S.(1996) “Asymptotic convergence in a generalized method predictorcorrector”. Mathematical programming,74,11-28.
[40] Muth, J.F.; Thompson, G.L.(1963). “Industrial Scheduling”. Prentice Hall,
Englewood Cliffs, N.J.
[41] Nesterov, Y.; Nemirovskii, A.S.(1994) “ Interior Point Polynomial Methods
in Convex Programming: Theory and Applications”. SIAM, Philadelphia, PA.
[42] Pinson, E.(1988)“Le Problème de Job-Sop”. Thèse de doctorat, Universitè Paris.
Referências Bibliográficas
89
[43] Potra,F. A.; Wright, S.J. (2000)“Interior-point methods”.Journal of Computational and Applied Mathematics, 124, 281-302.
[44] Ramos, A. D.(2002)“Método do Subgradiente Aplicado ao Job-Shop Decomposto
pela Tecnologia de Grupo e Relaxação Lagrangeana”. Dissertação de Mestrado,
Universidade Federal da Bahia.
[45] Renegar, J.(1988)“ A Polynomial-time Algorithm, Based on Newnton’s Method,
for Linear Programming”. Mathematical Programming, 40, 59-93.
[46] Santana, A. S.(2003)“Método de Decomposição de Dantzig-Wolfe Aplicado ao
Problema Combinatório de Job-Shop”. Dissertação de Mestrado, Universidade Federal da Bahia.
[47] Schaal, A.; M’Silti, H.; Tolla, P. (1993) “Modélisation et Systèmes Interactifs
de Stocksliés”. Technical Report, 117, Lamsade, Université Paris-Dauphine.
[48] Schaal, A. (1997) “Une Approche Hybride de Résolution de Problèmes Linéaires
en Nombres Entiers : Méthodes Intérieures et Méta Heuristiques”. PhD Thesis,
Univeristé Paris-Dauphine.
[49] Schaal, A.; M’Silti, H.; Tolla, P. (1997) “Une Approche Hybride de Résolution
de Problèmes Linéaires en Nombres Entier”. Technical Report, 145, Lamsade,
Université Paris-Dauphine.
[50] Schaal, A.; M’Silti, H.; Tolla, P. (1997) “Comparison of Simulated Annealing
and Genetic Algorithm Whith a Hybrid Method for General Integer Problems”.
Technical Report, 147, Lamsade, Université Paris-Dauphine.
[51] Schaal, A.; M’Silti, H.; Tolla, P. (1999) “Meta Heuristics Diversification of
Generalised Job-Shop Scheduling Based upon Mathematical Programming Techniques”. D.E.I.S. Universitá Di Bologna.
[52] Strusevich, V.A.(1997) “Shop scheduling problems under precedence constraints”. Annals of Operations Research, 69.
[53] Sousa, V.A.; Costa, G.R.M.(2001) “Aplicação dos Métodos de Pontos Interiores na resolução de Problemas Não Lineares, Não Convexos e de Grande Porte”.
XXXIII SBPO - Simpósio Brasileiro de Pesquisa Operacional.
Referências Bibliográficas
90
[54] Sousa, V.A.; Costa, G.R.M.(2003) “Um método para Determinação das Barras
Candidatas à Alocação de Reativos”. X Encuentro Regional Latinoamericano de
la Cigré, Puerto Iguazú, Argentina.
[55] Thompson, G.L.; Muth, J.F. (1963)“Industrial Scheduling”. Garnegie Institute of Technoly, 187-191.
[56] Vanderbei, R.J.; Shanno, D.F. (1999)“An Inerior-Point Algorithm for Nonconvex Nonlinear Programming”. J. Comput. Optm. Appl., 13, 231-253.
[57] Wright, S.J.(1997)“Primal-Dual Interior-Point Methods”. SIAM, Philadelphia,
PA.
[58] Yamada, T.; Nakano, R.(1997). “Genetic Algorithms for Job-Shop Scheduling
Problems”. Proc. of Modern Heuristics for Decision Suport, pages 67-81, UNICOM
seminar, 18-19 March 1997, London.
[59] Zwavaneld, C.M.; Van Wassenhove, L.N.; Sevast Javanov, S.V.; Potts,
C.N. (1995)“The two-stage assembly scheduling problem: Complexity and Approximation”. Operation Research, vol. 43.
[60] Zhao, G.(1996)“Interior Point Methods With Decomposition For Linear Programs”. Department of Mathematics National University of Singapoure.
Anexo A
Tópicos de Programação
Não-Linear
O objetivo neste anexo é apresentar alguma definições e teoremas referentes a
programação não linear que são importantes no escopo deste trabalho. As definições
aqui contidas têm como base os livros de Bazaraa [8] e Luenberg [34].
A.1
Tipos de Funções
Definição A.1. Seja S ∈ <n um conjunto convexo não vazio e, f : S → R, então
podemos dizer que:
• A função f é côncava em S se, dados x1 , x2 ∈ S então
f [λx1 + (1 − λ)x2 ] ≥ λf (x1 ) + (1 − λ)f (x2 )
para cada λ ∈ (0, 1).
• A função f é convexa em S se, dados x1 , x2 ∈ S então
f [λx1 + (1 − λ)x2 ] ≤ λf (x1 ) + (1 − λ)f (x2 )
para cada λ ∈ (0, 1).
Tópicos de Programação Não-Linear
92
• A função f é dita pseudoconvexa em x1 , x2 ∈ S se ∇f (x1 )T (x2 − x1 ) ≥ 0 implicar
que f (x2 ) ≥ f (x1 ).
Observação A.1.
Uma função convexa é pseudoconvexa conforme demonstrado em [8].
Teorema A.1. Seja S ∈ <n um conjunto convexo não vazio e, f : S → R sendo
duplamente diferenciável em S. Então, f é convexa se e somente se a sua matriz hessiana for positiva semidefinida para cada ponto de S. Analogamente, ela será côncava
se e somente se a sua matriz hessiana for negativa semidefinida.
Teorema A.2. Seja S ∈ <n um conjunto convexo não vazio e f : S → R sendo
diferenciável em S. Então, f é convexa se e somente se
f (y) − f (x) ≥ ∇f (x)T (y − x)
para qualquer x, y ∈ S. Analogamente, ela será côncava se e somente se
f (y) − f (x) ≤ ∇f (x)T (y − x)
para qualquer x, y ∈ S
Corolário A.1. Seja S ∈ <n um conjunto convexo não vazio e f : S → R linear,
então f é convexa e côncava simultaneamente.
As demonstrações dos teoremas A.1 e A.2 podem ser encontradas em Bazaraa
[8].
A.2
Condições de Otimalidade para Problemas com
Restrições
Definição A.2. Seja g(x) : Rm →R uma função diferenciável. Um ponto x satisfazendo a restrição g(x) = 0 é chamado de ponto regular da restrição se os vetores
gradientes ∇g1 (x), ∇g2 (x), ..., ∇gm (x) são linearmente independentes.
Tópicos de Programação Não-Linear
93
Teorema A.3. Condição de Primeira Ordem (Restrições de Igualdade)
Tome x sendo um ponto extremo local de f restrito a g(x) = 0. Assumindo
que x seja um ponto regular destas restrições (g(x) = 0). Então, existe y ∈ Rm tal que
∇f (x) + y T ∇g(x) = 0
Neste contexto é conveniente introduzir o Lagrangeano associado com o problema restrito, definido como:
L(x, y) = f (x) + y T g(x)
As condições necessárias podem ser expressas como:
∇Lx (x, y) = 0
∇Ly (x, y) = 0
Teorema A.4. Condições Necessárias de Karush-Kuhn-Tucker (KKT) Seja X
um conjunto aberto não vazio em Rn , e tome f : Rn →R e gi : Rn →R para i = 1, ..., m.
Considere o problema P de minimizar f (x) sujeito a x ∈ X e gi (x) ≤ 0 par i = 1, ..., m.
Considere x sendo uma solução factı́vel e denote I = {i : gi (x) = 0}. Suponha que f e
gi para i = 1, ..., m são diferenciáveis em x. Além disto, suponha que ∇gi (x) par i ∈ I
são linearmente independentes. Se x é solução local do problema P , então existem
escalares ui ∀i ∈ I tal que:
∇f (x) +
P
i∈I
ui ∇gi (x) = 0
ui gi (x) = 0
para i = 1, ..., m
ui ≥ 0
para i = 1, ..., m
A prova completa deste teorema pode ser encontrada em [34] e [8].
As condições de KKT podem alternativamente ser escritas de forma vetorial,
assumindo as condições anteriores, como:
∇f (x) + ∇g(x)T u = 0
uT g(x) = 0
u≥0
Tópicos de Programação Não-Linear
94
Onde g(x)T é a transposta da jacobiana de g em x e u é um vetor com os multiplicadores
de Lagrange.
Teorema A.5. Condições Suficientes de Segunda Ordem (Restrições de Igualdade)
Suponha que exista um ponto x satisfazendo g(x) = 0, e x ∈ Rm tal que
∇f (x) + y T ∇g(x) = 0
Suponha também que a Hessiana do Lagrangeano
H(x) = ∇2 f (x) +
m
X
yi ∇2x gi (x)
i=1
seja positiva definida em M = {y : ∇g(x)y = 0}, isto é, para y ∈ M e y 6= 0, então
y T H(x)y > 0. Então x é um ponto de mı́nimo local de f sujeito a g(x) = 0.
Teorema A.6. Seja X ∈ <n um conjunto aberto não vazio, e tome as funções f :
<n → R e gi : <n → R, i = 1, ..., m. Considere o problema P de minimizar f (x)
sujeito a x ∈ X e gi (x) ≤ 0 para i = 1, ..., m. Considere x sendo uma solução que
atenda às condições de KKT A.4 e denotemos I = {i : gi (x) = 0}. Então se f é
pseudoconvexa em x, e se gi , i ∈ I são convexas em x, logo x é uma solução ótima
global para o problema P .
Prova
Tome x sendo uma solução factı́vel para o problema P . Para i ∈ I, gi (x) ≤
g( x), e como gi (x) ≤ 0 e gi (x) = 0 então, pela convexidade de gi em x, temos que
∇gi (x)T (x − x) ≤ gi (x) − gi (x) ≤ 0
(A.1)
Multiplicando pelos respectivos multiplicadores de Lagrange yi referentes às condições
P
de KKT do ponto x, nós temos [ i∈I yi ∇gi (x)T ](x − x) ≤ 0. Mas desde que ∇f (x) +
P
T
i∈I yi ∇gi (x) = 0, segue que ∇f (x)(x − x) ≥ 0. Então, pela pseudoconvexidade de
f em x, nós temos que f (x) ≥ f (x), o que completa a prova.
Tópicos de Programação Não-Linear
95
Retornando ao problema (3.1) verificamos que suas restrições diferem em
relação ao teorema A.6 por serem restrições não negativas. Isto implica que equação
A.1 não é verdadeira. Como gi (x) ≥ 0, temos
∇gi (x)T (x − x) ≥ gi (x) − gi (x) ≥ gi (x) ≥ 0
Desta forma, não há garantia quanto ao sinal de [
P
i∈I
(A.2)
yi ∇gi (x)T ](x − x) e por
conseguinte, não podemos afirmar que um ponto que atenda à primeira condição de
KKT seja um ponto ótimo para o problema de job-shop.
A.3
Regra de Armijo
Existem várias regras para a seleção do passo α em algoritmos de busca em
linha. A regra de Armijo é uma regras mais simples e eficaz. Ela será usada na redução
do passo α com a finalidade de garantir a convergência a cada iteração do método de
pontos interiores conforme apresentado na seção 3.2.1.
A idéia básica desta regra é garantir que o tamanho do passo não seja tão
grande nem tão pequeno. Consideremos um ponto z k e uma direção primal 4pk tais
que ∇f (z k ) 6= 0, < ∇f (z k ), 4pk >< 0 e α ∈ (0, 1).. Existe χ = χ(α) > 0 tal que:
f (z k + α4pk ) − f (z k ) ≤ ηα < ∇f (z k ), 4pk >, η ∈ (0, χ)
Essa condição evita passos grandes. Porém, passos pequenos são inevitáveis,
simplesmente porque passos grandes podem não permitir um decréscimo adequado,
mas é importante tentá-los. Por isso assumimos o primeiro passo sendo η k = 1 e
diminuı́mos o passo sem exageros até que a condição de Armijo seja satisfeita.
A.4
Função de mérito
Vejamos a definição de função de penalidade conforme Luenberg [34]:
Tópicos de Programação Não-Linear
96
Definição A.3. Sendo f e g funções contı́nuas em <n , considere o problema:
M in. f (x)
s.a.
(A.3)
g(x) = 0
A função de penalidade (mérito) permite trocar o problema (A.3) por um problema
irrestrito da forma
Minimizar f (x) + cP (x)
(A.4)
onde c é uma constante positiva e P é uma função em <n satisfazendo:
• P é contı́nua,
• P (x) ≥ 0
∀x ∈ <n ,
• P (x) = 0 se e somente se g(x) = 0.
Idealmente, quando c → ∞ o ponto de solução do problema penalizado A.4
convergirá para a solução do problema restrito A.3.
Anexo B
Algoritmos Sugestivos
B.1
Algoritmo para ajuste da matriz Normal Nβ
Inı́cio
Tome
b = N,
N
χ=0
ξ = 4. max(|hii |),
Enquanto
χ > 0,
C = 0n×n
então:
H = H + 4λξI;
Para i = 1, 2, ..., n
y = y + c(k, i)2 ;
χ = h(i, i) − y;;
se χ > 0, então
cii =
√
A
x=0;
Para j = 1 : n,
para k = 1 : i − 1,
x= x+(c(k,i)c(k,j));
se i < j então
c(i, j) = (h(i, j) − x)/c(i, i)
se i > j então c(i,j)=0
se χ ≤ 0 então faça ξ =
Fim
N = CT C
xi+1
100
Algoritmos Sugestivos
B.2
98
Algoritmo sugestivo de MPI
Este algoritmo é uma adaptação do algoritmo proposto por Griva, et al [28] e
foi usado para resolução do problema-exemplo 2 na seção 3.2.3.
Passo 1:
Inicialização:
São dados:
Uma aproximação primal-dual z 0 = (t0 , s0 , y 0 ) = (p0 , y 0 )
Uma constante ε > 0 usada como critério de parada,
Parâmetros 0 < η < 1; 0 < δ < 1; 0 < q < 1; ς > 0
Tome:
¾
1
, l := 0
z := z , τ := ν(z ), µ := δτ, τµ = νµ (z ), β := max 2µr0 ,
τµ
0
½
0
0
Passo 2:
Se τ ≤ ε, Pare. Saı́da: z.
Passo 3:
Ajuste da matriz Normal conforme algoritmo apresentado seção anterior
Descubra a direção primal 4z
Defina l := l + 1 e κ := max{0, 95, 1 − τ }.
p
d
Defina os tamanhos de passo αp := αmax
eαd := αmax
Defina pe := p + αp 4p, ye := y + αd 4y
Passo 4:
Reduza αp até que Lβ,µ (p + αp 4p, y) − Lβ,µ (p, y) ≤ ηαp < ∇Lβ,µ (p, y), 4p >
Faça pe := p + αp 4p
Passo 5:
Se ||∇p Lβ,µ(pe,y) || > ς||ρ(e
p)|| ou y + βρ(e
p) 0 vá para Passo 3.
Passo 6:
ye := y + βρ(e
p).
Se νµ (e
z ) > qτ , Tome p := pe, β := 2β, vá para o passo 2.
Passo 7:
Se ν(e
z ) ≤ qτ , tome τ := ν(e
z ), µ := δτ.
¾
½
1
Tome z := ze, τµ := νµ (e
z ), β := max β,
τµ
Passo 8:
Se τ ≤ ε, Pare. Saı́da: z.
Passo 9:
Vá para o Passo 3
Universidade Federal da Bahia-UFBa
Instituto de Matemática/Depto. de Matemática
Campus de Ondina, Av. Adhemar de Barros s/n, CEP:40170-110
www.im.ufba.br/hpinst/mestrado