movimento parabolico

Pro. Robinson, DEFIJI
MOVIMENTO PARABÓLICO
1.
INTRODUÇÃO
Qualquer objeto lançado de forma obliqua ou horizontal e próximo à superfície da terra pode ser
considerado um projétil, cujo movimento é descrito pela composição vetorial de um MRU na direção
horizontal e de um MRUV na direção vertical. Desprezando a força da resistência do ar, a trajetória do
projétil tem a forma de uma parábola cujos pontos são definidos pelas equações
= + (1)
e
= + − (2)
Onde e são as coordenadas do ponto de lançamento, e são as projeções do vetor
velocidade inicial sobre os eixos coordenados, g é a aceleração da gravidade, e t é o temo do
movimento transcorrido. A figura 1 representa a trajetória de um projétil lançado obliquamente a partir
da origem do sistema de coordenadas. Eliminando a variável do tempo nas equações 1 e 2
conseguimos a equação da trajetória parabólica do projétil.
= tan − (3)
Figura 1. Trajetória de um projétil para = = 0.
OBSERVAÇÕES:
1- Quando queremos calcular o alcance horizontal R, fazemos:
− = cos = E calculamos R da equação 3, quando − = 0. Desse modo, obtemos a equação:
=
2
sen cos Pro. Robinson, DEFIJI
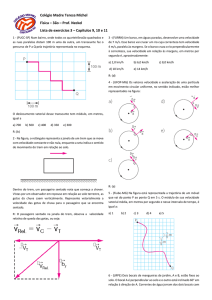
2- Se o projétil for lançado horizontalmente ( = "#" = 0), partindo do ponto de
coordenadas e = $, a equação da parábola que descreve a trajetória é:
=$−
2
O gráfico dessa equação é mostrado na figura 2.
y
vo
H
R
x
Figura 2. Trajetória de um projétil disparado horizontalmente.
2.
OBJETIVO
Esta atividade experimental visa contribuir a compreensão das equações que regem os
movimentos parabólicos por meio do lançamento de uma esfera metálica, em distintos ângulos. Diante
disto, o objetivo deste experimento verificar a cinemática de um projétil e determinar a velocidade de
lançamento de um projétil, tendo medido o seu alcance e altura de Vôo. Alem disto, verificar que a
trajetória do movimento é parabólica.
3.
PROCEDIMENTO EXPERIMENTAL
Experimento 1
(a) Coloque o dispositivo de lançamento inicialmente na inclinação de zero grau e escolha um sistema
de referência de modo que possa medir, neste sistema, a altura inicial de lançamento e o alcance.
Figura. Lançador de projeteis
Pro. Robinson, DEFIJI
(b) Escolha a primeira altura de vôo como 10 cm e lance a bola para as três primeiras posições
distintas da mola (do lançador), medindo para cada uma delas o alcance da bola e anotando todos os
dados na folha de relatório.
(c) Repita o procedimento para as outras três alturas de vôo (15cm, 20cm e 30cm).
(d) Trace um gráfico numa folha de papel milimetrado, para cada posição da mola para o lançamento
da esferinha, a posição y versus x. Comente sobre a curva obtida.
Experimento 2
(a) Escolha um ângulo que esteja entre 0o e 90º para o lançamento. Faça a previsão teórica da posição
onde a esferinha deverá cair e coloque o copo plástico no local indicado de modo de poder verificar se
seus cálculos estão corretos (caso estejam corretos, a esfera deverá cair dentro do mesmo). É
necessário levar em consideração, nos seus cálculos, as dimensões do copo e da esferinha?
(b) É possível obter a velocidade (módulo e direção) da esferinha no instante em que ela toca a mesa?
Justifique qualitativamente e/ou quantitativamente.