NUCLEO_COM_ENTREFERR0

NÚCLEO COM ENTREFERRO
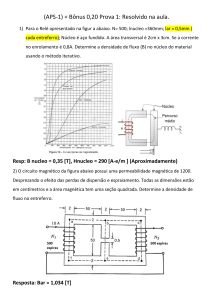
Determinar a corrente necessária para gerar no entreferro um fluxo de 
= 1,78 x 106 linhas, conforme circuito abaixo.
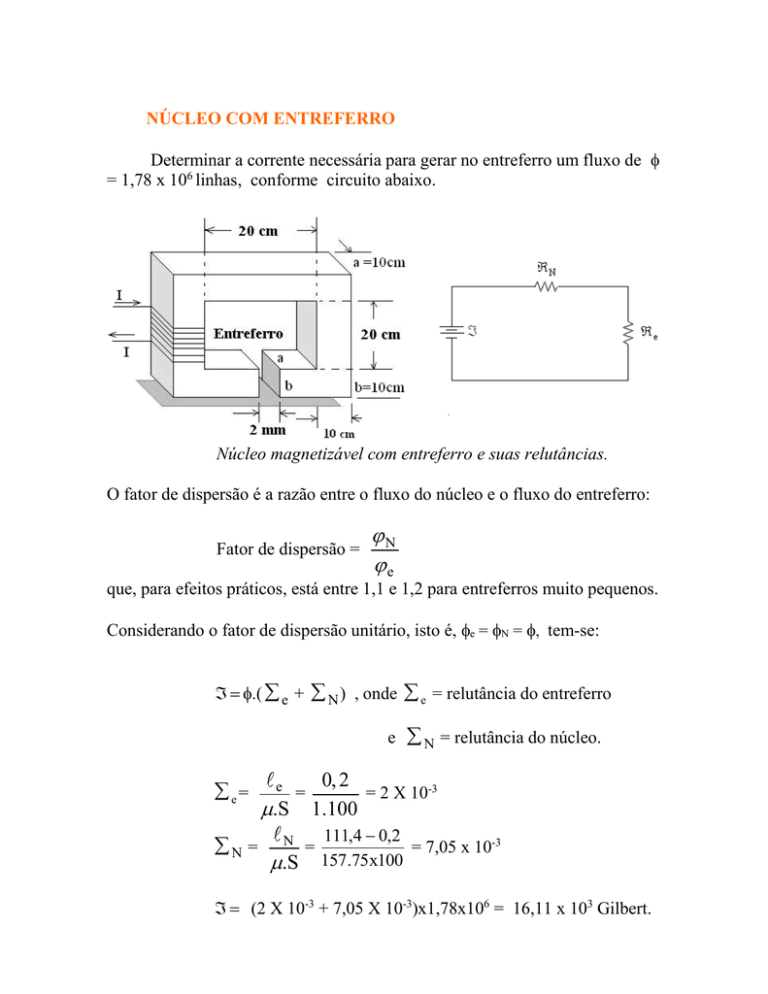
Núcleo magnetizável com entreferro e suas relutâncias.
O fator de dispersão é a razão entre o fluxo do núcleo e o fluxo do entreferro:
Fator de dispersão =
jN
je
que, para efeitos práticos, está entre 1,1 e 1,2 para entreferros muito pequenos.
Considerando o fator de dispersão unitário, isto é, e = N = , tem-se:
  .(  e +  N ) , onde  e = relutância do entreferro
e  N = relutância do núcleo.
Âe =
ÂN =
e
m.S
N
=
m.S
0, 2
= 2 X 10-3
1.100
=
111,4  0,2
= 7,05 x 10-3
157.75x100
  (2 X 10-3 + 7,05 X 10-3)x1,78x106 = 16,11 x 103 Gilbert.
16,11x10 3
→ I = 12,82 A
  1,257xN.I  I =
1,257 x1000
Outra forma de se resolver
Núcleo magnetizável com entreferro e suas relutâncias.
Seja:
HN: o campo gerado no núcleo
He : o campo gerado no entreferro;
 N : o comprimento do núcleo;
 e : o comprimento do entreferro.
Podemos escrever:
1,257.N.I = HN.  N + He.  e (GGS)
Sem considerar a dispersão do entreferro, tem-se:

BN = Be = , onde S = a.b = 100 cm2
S
1,78x10 6
BN =
= 1,78 x 104 Gauss = 1,78 T
100
B
1,78x10 4
HN = N =
= 112,84 Oe
157 ,75

BN
1,78x10 4
He =
=
= 1,78 x 104 Oe
 o (ar )
1
Logo a corrente que precisa circular pela espira para gerar o fluxo  = 1,78 x
106 linhas é:
H N . N  H e . e
112,84 x(111,4,0,2)  1,78x10 4 x 0,2
I =
=
1257
1,257 xN
I = 12,82
Considerando a dispersão de linhas no entreferro, um dos procedimentos é
se levar em conta que densidade de linhas no núcleo é 20% maior que a
densidade de linhas no entreferro se este tiver um comprimento bem menor
que o comprimento do núcleo. Assim:
BN = 1,2xBe = 1,2x1,78x106 = 2,136 x106
Logo,
2,136 x10 4
HN =
= 135,40 Oe
157 ,75
O campo no entreferro é mesmo. Logo,
I=
135,40 x(111,4,0,2)  1,78x10 4 x 0,2
= 14,8 A
1257
Fluxo magnético com dispersão de fluxo magnético no entreferro
`