Circuitos Magnéticos Exemplos Arquivo

SEL 329 – CONVERSÃO
ELETROMECÂNICA DE ENERGIA
Aula 03
Circuitos Magnéticos
Revisão Aula Passada
•
Aplicação da Lei Circuital de Ampère – Exemplo 2
 H.dl  Ni
BH
Ni
H
lc
[Wb/m2]
[A.esp/m]
Revisão Aula Passada
Analogia entre circuitos elétricos e magnéticos
ELÉTRICO
MAGNÉTICO
Densidade de corrente: J(A/m2)
Densidade de fluxo magnético: B (Wb/m2)
Corrente: I (A)
Fluxo magnético: Φ (Wb)
Intensidade de campo elétrico: ε (V/m)
Intensidade de campo magnético: H (A/m)
Tensão ou fem: E (V)
Força magnetomotriz ou fmm: F (A.e)
Condutividade: σ (A/[Vm])
Permeabilidade: μ (Wb/[Am])
Resistência: R (Ω)
Relutância: R (A.e/Wb)
1
1
Resistividade:  
Relutividade =


Condutância: G (S)
Permeância: P (Wb/A.e)
E = R.I
F = N.I = R.Φ
l
l
R=
R= m
 A
A
Comportamento magnético de materiais ferromagnéticos
A curva de magnetização satura pois todos os domínios magnéticos já estão
alinhados
Impacto de um campo magnético nos domínios magnéticos
(a) H = 0
(b) H = fraco
(c) H = moderado
(d) H = elevado
Curva de Magnetização
Fmm   
 ( wb )
Fmm (A-e)
Curva de Magnetização
BH
- Ao aumentar-se a corrente, a intensidade de campo H aumenta.
- E a densidade de fluxo magnético B?
Densidade de Fluxo, [T]
Curva de Magnetização para um material típico de aço
Intensidade do campo magnético H, [A-e/m]
μr adimensional
Permeabilidade Relativa μr para um material típico de aço
Intensidade do campo magnético H, [A-e/m]
Curva de Magnetização
Permeabilidade magnética
Nos materiais ferromagnéticos,  é diversas milhares de vezes maior do que 0
r
Ferro
5000
Ferro-silício
7000
Permalloy (70-90% Ni)
10000
Classificação de Materiais Magnéticos
Materiais diamagnéticos: permeabilidade relativa < 1 (Exemplos: cobre, água,
mercúrio, ouro, prata)
Materiais paramagnéticos: permeabilidade relativa ≈ 1 (Exemplos: alumínio,
manganês, estanho, cromo, platina, paládio, oxigênio líquido)
Materiais ferromagnéticos: permeabilidade relativa >> 1 (Exemplos: ferro,
aços especiais, cobalto, níquel, ligas como Alnico)
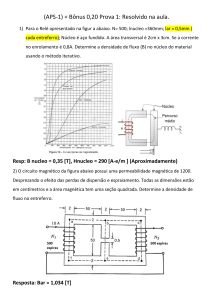
Exemplo 5 (Livro P. C. Sem Exemplo E1.1)
Para o Relé apresentado na figur a abaixo.
N= 500; lnucleo =360mm; lar = 1,5mm (cada entreferro), B =0,8[T]; Núcleo é aço fundido.
A área transversal é 2cm x 3cm:
a) Determine: a corrente contínua necessária para atuar o relé
b) Os valores de permeabilidade e permeabilidade relativa do núcleo;
c) Corrente necessária para produzir a mesma corrente de fluxo para o caso sem entreferro;
d) Valor da relutância do núcleo e do entreferro.
Exemplo 5
N= 500; lnucleo =360mm; lar = 1,5mm, B =0,8[T]; Núcleo é aço fundido. A área
transversal é 2cm x 3cm
Resposta:
a) I = 4,19 A.
b) μnuclelo = 1,57 x 10^-3 (wb/(A-m) ou (H/m)
c) Sem entreferro; I = 0,368 A
d) Relutância : Rnúcleo = 0,38x10^-6 [A-e/wb]
Rar = 1,99 x 10^-6 [A-e/wb]
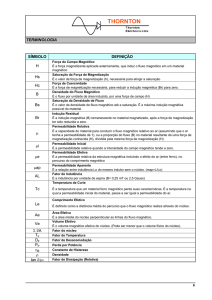
Exemplo 6
No problema anterior, N= 500; lnucleo =360mm; lar = 1mm (cada
entreferro); Núcleo é aço fundido. A área transversal é 2cm x 3cm.
Se a corrente no enrolamento é 4A e cada entreferro é 1mm.
Determine B no núcleo do material.
Resposta:
Bnucleo = 1,08 T.
Refazer para:
a) Mesmas condições do problema 6 mudando apenas i =
0,8A.
Resp: B = 0,2[T]; H = 200 [A-e/m] aprox
b) Mesmas condições do problema 6 mudando apenas i =
0,8A e cada entreferro é 0,5mm.
Resp: B = 0,35[T]; H = 290 [A-e/m] aprox
Resposta:
Bnucleo = 1,08 T.
Refazer para:
a) Mesmas condições do problema 6 mudando apenas i =
0,8A.
Resp: B = 0,2[T]; H = 200 [A-e/m] aprox
b) Mesmas condições do problema 6 mudando apenas i =
0,8A e cada entreferro é 0,5mm.
Resp: B = 0,35[T]; H = 290 [A-e/m] aprox