O Entreferro - IFSC Campus Joinville

MINISTÉRIO DA EDUCAÇÃO
SECRETARIA DE EDUCAÇÃO PROFISSIONAL E TECNOLÓGICA
INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DE SANTA CATARINA
CAMPUS JOINVILLE
DEPARTAMENTO DO DESENVOLVIMENTO DO ENSINO
COORDENAÇÃO ACADÊMICA
EletroEletronica
Circuitos Magnéticos
Prof. Luis S. B. Marques
Relação entre o campo e a
corrente
 
B

d
l


i

Bl  iN
Hl  iN
B  H
Hl  Ni
Relutância Magnética
l

A
É definida como a oposição que um determinado trecho
do circuito magnético oferece à circulação do fluxo
magnético.
Permeabilidade magnética
   R  o
• Define-se permeabilidade magnética (µ) de um
dado material como a habilidade deste material
ser magnetizado ou a habilidade de conduzir
linhas magnéticas de força em comparação com
o ar e o vácuo.
Permeabilidade magnética
o  4   10
7
2000  R  80.000
O Entreferro
Os sistemas de conversão
de energia que utilizam
partes móveis possuem um
entreferro inserido em seu
circuito magnético.
Quando o entreferro é muito menor que a área da
seção transversal é possível considerar que a área
para o entreferro é igual à área da seção transversal
para o material magnético.
O Entreferro
A densidade de fluxo no material
magnético é dada por:
A densidade de fluxo no entreferro
é dada por:
Como as áreas são iguais,
então:
Bc 
Bg 

Ac

Ag
Bc  Bg 

A
O Entreferro
Quando o comprimento do
entreferro é suficientemente
grande que se torna
necessário considerar o
efeito do espraiamento, o fazse através da adição do
comprimento do entreferro a
cada dimensão relativa ao
cálculo da área da seção
transversal.
Ag  (a  g )  (b  g )
O Espraiamento
Circuito magnético com entreferro
N  i  H c  lc  H g  g
N i 
Bc

 lc 
Bg
o
g
j = Bc × Ac = Bg × Ag
lc
g
N i 
 

  Ac
o  Ag
 lc
g 
N i    


   Ac  o  Ag 
Equação para cálculo do fluxo
magnético
Definindo a relutância do
material magnético.
lc
c 
  Ac
Definindo a relutância do
entreferro.
g
g 
o  Ag
N  i    (c   g )
Analogia entre circuito
elétrico e circuito magnético
φ
i
E
R
NI
R
Força eletromotriz eficaz
induzida em cada enrolamento
E1 = 4, 44× f × jmax × N1 E2 = 4, 44× f × jmax × N2
Exercício: O solenóide mostrado na figura abaixo possui 250 espiras. Como o
comprimento é muito maior que o diâmetro, o campo magnético no interior do
solenóide pode ser considerado uniforme. Determine a intensidade de campo
magnético e a densidade de fluxo no interior do solenóide, assim como a
indutância deste solenóide. Despreze o campo magnético no exterior do
solenóide. A corrente é igual a 10A.
B  H
B  4 10 5000
7
B  6,28mT
Hl  Ni
H  0,5  250 10
H  5000 A / m
N NBA
L

i
i
250  6,28 10    (2,5 10 )
L
 308H
10
3
2 2
Exercício: A profundidade do núcleo mostrado na figura abaixo é igual a 10cm. A
permeabilidade relativa do material é igual a 2500, o número de espiras igual a
300 e a corrente que alimenta o circuito igual a 1 ampère. Determine o fluxo
magnético no núcleo e a densidade de fluxo magnético nas partes do núcleo.
l
0,35
1 

7
A 2500  4 10  0,015
1  7,43kA/ Wb
l
0,4
2 

A 2500  4 10 7  0,01
2  12,7kA/ Wb
  21  22  40,34kA/ Wb
Exercício: A profundidade do núcleo mostrado na figura abaixo é igual a 10cm. A
permeabilidade relativa do material é igual a 2500, o número de espiras igual a
300 e a corrente que alimenta o circuito igual a 1 ampère. Determine o fluxo
magnético no núcleo e a densidade de fluxo magnético nas partes do núcleo.
Ni  
300

 7,44mWb
40,34k

7,44m
B1 

 0,495T
A1 0,015
7,44m
B2 
 0,74T
0,01
Exercício: No circuito magnético abaixo o núcleo é fabricado com chapas de aço silício
e possui seção quadrada. As correntes nos enrolamentos são i1=0,33A e i2=
0,6A. Determine a densidade de fluxo no raio médio do núcleo. Considerando
essa densidade de fluxo, determine o fluxo no núcleo.
Exercício: No circuito magnético abaixo o núcleo é fabricado com chapas de aço silício
e possui seção quadrada. As correntes nos enrolamentos são i1=0,33A e i2=
0,6A. Determine a densidade de fluxo no raio médio do núcleo. Considerando
essa densidade de fluxo, determine o fluxo no núcleo.
Hl  Ni
H  2R  N1i1  N2i2
H  2 0,2  600  0,33  300  0,6
B  1,1T
H  300 A / m
  BA
  1,1 4 10
4
  4,4 10 Wb
4
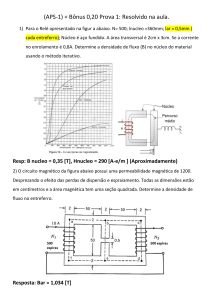
Exercício: O toróide mostrado na figura abaixo é fabricado com ferro muito
puro. Determine: A corrente necessária para produzir uma densidade
de fluxo igual a 1,2T no raio médio do toróide, sabendo que μr=8000.
Qual o fluxo no núcleo?
Se um entreferro igual a 2mm é inserido no toróide, determine o valor
da corrente necessária para manter a densidade de fluxo igual a 1,2T.
Exercício:O circuito magnético mostrado na figura abaixo possui número de espiras
igual a 500 e a corrente igual a 20A. O material do núcleo possui relutância
desprezível. Determine o valor máximo para o entreferro para que uma
densidade de fluxo de 1,4T seja estabelecida, considerando que a perna central
possui o dobro da dimensão das pernas laterais.