Colégio Centro Morumbi Cursinho do GEB Lei dos

Colégio Centro Morumbi
Cursinho do GEB
Lei dos Senos e Cossenos
Lista de Exercícios – Parte 1
1)
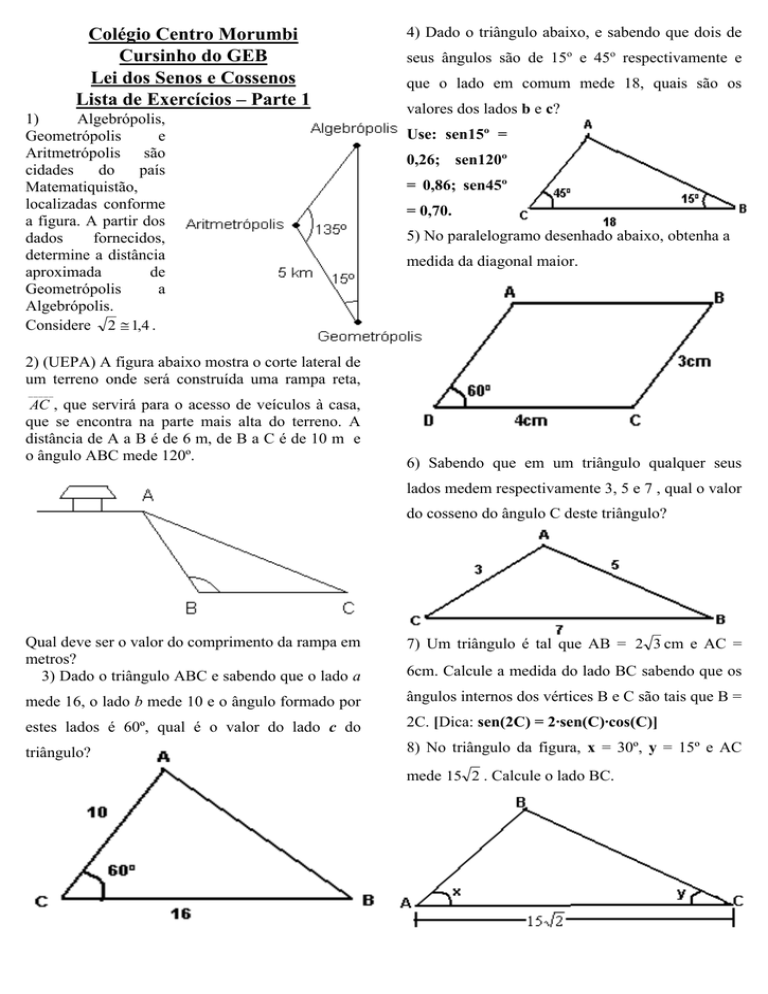
Algebrópolis,
Geometrópolis
e
Aritmetrópolis são
cidades
do
país
Matematiquistão,
localizadas conforme
a figura. A partir dos
dados
fornecidos,
determine a distância
aproximada
de
Geometrópolis
a
Algebrópolis.
Considere 2  1,4 .
4) Dado o triângulo abaixo, e sabendo que dois de
seus ângulos são de 15o e 45o respectivamente e
que o lado em comum mede 18, quais são os
valores dos lados b e c?
Use: sen15º =
0,26; sen120º
= 0,86; sen45º
= 0,70.
5) No paralelogramo desenhado abaixo, obtenha a
medida da diagonal maior.
2) (UEPA) A figura abaixo mostra o corte lateral de
um terreno onde será construída uma rampa reta,
_____
AC , que servirá para o acesso de veículos à casa,
que se encontra na parte mais alta do terreno. A
distância de A a B é de 6 m, de B a C é de 10 m e
o ângulo ABC mede 120º.
6) Sabendo que em um triângulo qualquer seus
lados medem respectivamente 3, 5 e 7 , qual o valor
do cosseno do ângulo C deste triângulo?
Qual deve ser o valor do comprimento da rampa em
metros?
3) Dado o triângulo ABC e sabendo que o lado a
7) Um triângulo é tal que AB = 2 3 cm e AC =
mede 16, o lado b mede 10 e o ângulo formado por
ângulos internos dos vértices B e C são tais que B =
estes lados é 60º, qual é o valor do lado c do
2C. [Dica: sen(2C) = 2∙sen(C)∙cos(C)]
triângulo?
8) No triângulo da figura, x = 30º, y = 15º e AC
6cm. Calcule a medida do lado BC sabendo que os
mede 15 2 . Calcule o lado BC.
9) Considere um triângulo cujos lados medem 5cm,
6cm e 9cm. Qual a área de um quadrado cujo lado é
a mediana relativa ao maior lado do triângulo
considerado em centímetros quadrados?
10) Calcule o cosseno do ângulo obtuso x do
triângulo ABC.
14)
Um
topógrafo
pretende
medir
a
distância
entre
dois
pontos (A e
B) situados
em margens
opostas
de
um rio.
Para isso, ele escolheu um ponto C na margem em
que está, e mediu os ângulos ACˆ B e CAˆ B ,
encontrando, respectivamente, 45° e 75º.
_____
11) Calcule os lados AC e BC do triângulo abaixo,
bem como seu perímetro.
_____
Determine AB , sabendo que AC mede 16 m.
(Utilize 2  1,4 ).
15) Calcule a distância dos pontos A e B, entre os
quais há uma montanha, sabendo que suas
distâncias a um ponto fixo M são de 2 km e 3 km,
respectivamente. A medida do ângulo AMˆ B é igual a
60º.
12) Calcule o valor de
cos(x) no triângulo da
16) Determine a distância d indicada na figura.
figura.
13) Uma certa propriedade rural tem o formato de
um trapézio como na figura. As bases WZ e XY do
trapézio medem 9,4 km e 5,7 km, respectivamente,
e o lado YZ margeia um rio. Se o ângulo XYZ é o
dobro do ângulo XWZ, a medida, em km, do lado
YZ que fica à margem do rio é:
75
d
300m
45
Respostas: 1. D = 7,0 m; 2. D = 14 m; 3. D = 14
m; 4. b = 5,44 m e c = 14,65 m; 5. D = √37 m;...
(A) 7,5. (B) 5,7. (C) 4,7. (D) 4,3. (E) 3,7.
. (Dado: use as aproximações sen(59°) ≈
0,87 e sen(64°) ≈ 0,90)
Colégio Centro Morumbi
Cursinho do GEB
Lei dos Senos e Cossenos
Lista de Exercícios – Parte 2
distância
1) Os lados de um triângulo são 3, 4 e 6. O cosseno
do maior ângulo interno desse triângulo vale:
a) 11/24
b) - 11/24
c) 3/8
d) - 3/8 e) - 3/10
2) Em um paralelogramo ABCD, os lados AB e
AD medem, respectivamente, x 2 cm e x cm, e θ é o
ângulo agudo formado por esses lados. Se a diagonal
maior mede 2x cm, então o ângulo θ é tal que
14
2
b) sen θ = 4
4
1
d) sen θ =
e) tg θ =
2
a) cos θ =
c) cos θ =
3
2
3) Num paralelogramo, cada ângulo agudo mede 30º
e os lados que formam cada um desses ângulos
medem 3 3 cm e 5 cm. Calcule a medida da menor
das diagonais desse paralelogramo.
a) 6 cm b) 3 cm c) 3 3 cm d) 7 cm
e) 15 3 cm
4) Na figura abaixo, o triângulo ABC é um triângulo
equilátero de 3 cm de lado, e o triângulo retângulo
BCD tem lados BD = 4 cm e CD = 5 cm e
= 90°.
Qual a medida do segmento AD?
a) 3
b) 4 3
c) 100  3
d) 25  12 3
e) 2 3
5) A perímetro do triângulo a seguir é:
a)20
b)30 c) 40 d)36 e)18
6) Uma ponte deve ser construída sobre um rio,
unindo os pontos A e B, como ilustrado na figura a
seguir. Para calcular o comprimento AB, escolhe-se
um ponto C, na mesma margem em que B está, e
medem-se os ângulos C A = 57° e A B = 59°.
Sabendo que
mede 30m, indique, em metros, a
7) (Fuvest) No quadrilátero a seguir, BC = CD = 3
cm, AB = 2 cm, A C = 60° e A C = 90°.
A medida, em cm, do perímetro do quadrilátero é:
a) 11
b) 12
c) 13
d) 14
e) 15
8) Se em um triângulo ABC o lado
mede 3 cm, o
lado
mede 4 cm e o ângulo interno formado entre
os lados
e
mede 60°, então o lado
mede:
a)
cm
b)
cm c) 2 cm d) 33 cm e)
22 cm
9 )(Fuvest) Na figura abaixo, tem-se
= 3,
=4e
= 6.
O valor de
é:
Dica! (Ache, pela lei dos cossenos, o cosseno do
ângulo A B, no triângulo ABC).
a) 17/12
b) 19/12
c) 23/12
d) 25/12
e) 29/12
10) (Unesp) Dois terrenos, T2 e T2, têm frentes para
a rua R e fundos para a rua S, como mostra a figura.
O lado BC do terreno T1 mede 30 m e é paralelo ao
lado DE do terreno T2. A frente AC do terreno T1
mede 50 m e o fundo BD do terreno T2‚ mede 35 m.
Ao lado do terreno T2‚ há um outro terreno, T3, com
frente para a rua Z, na forma de um setor circular de
centro E e raio ED.
Determine:
a) as medidas do fundo AB do terreno T1 e da frente
CE do terreno T2.
b) a medida do lado DE do terreno T‚ e o perímetro
do terreno T3.
11) (Fuvest) Em uma semicircunferência de centro C
e raio R, inscreve-se um triângulo equilátero ABC.
Seja D o ponto onde a bissetriz do ângulo ACB
intercepta a semicircunferência. O comprimento da
corda AD é:
a) R√(2 - √3) b) R√[(√2) - 1] c) R√(3-√2)
d) R√[(√3) - (√2)] e) R√[(√3) - 1]
12) Um dos ângulos internos de um paralelogramo de
lados 4 m e 6 m mede 120°. A maior diagonal desse
paralelogramo mede, em metros:
a) 2√17
b) 2
c) 2√21 d) 2√23
e) 3
13) Para calcular a distância entre duas árvores
situadas nas margens opostas de um rio, nos pontos A
e B, um observador que se encontra junto a A afastase 20 m da margem, na direção da reta AB, até o
ponto C e depois caminha em linha reta até o ponto
D, a 40 m de C, do qual ainda pode ver as árvores.
Tendo verificado que os ângulos DCB e BDC
medem, respectivamente, cerca de 15° e 120°, que
valor ele encontrou para a distância entre as árvores,
se usou a aproximação 6 = 2,4?
14) (Fuvest) – As páginas de um livro medem 1
dm de base e (1  3) dm de altura. Se este livro
foi parcialmente aberto, de tal forma que o ângulo
entre duas páginas seja 60°, a medida do ângulo α,
formado pelas diagonais das páginas, será:
a) 15°
b) 30°
c) 45°
d) 60° e) 75°
Respostas: 1 (a); 2 (b); 3 (d); 4 (d); 5 (a); 6 d
= 29 m; 7 (b); 8 (b); 9 (e); 10 a) AB = 70 m;
CE = 25 m; b) DE = 45 m e P = 15∙(6 + π) m;
11 (a); 12 (b); 13. Resp: d = 28 m; 14 (b).