Problemas Resolvidos de Física

Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
RESNICK, HALLIDAY, KRANE, FÍSICA, 4.ED., LTC, RIO DE JANEIRO, 1996.
FÍSICA 1
CAPÍTULO 2 – MOVIMENTO UNIDIMENSIONAL
74. Uma bola de aço de rolamento é largada do teto de um edifício com velocidade inicial nula. Um
observador em pé diante de uma janela com 120 cm de altura nota que a bola gasta 0,125 s para
ir do topo da janela ao parapeito. A bola continua a cair, chocando-se elasticamente com uma
calçada horizontal e reaparece no parapeito da janela 2,0 s após passar por ela ao descer. Qual a
altura do edifício? (Após uma colisão elástica, a velocidade escalar da bola em dado ponto é a
mesma ao subir e ao descer.)
(Pág. 33)
Solução.
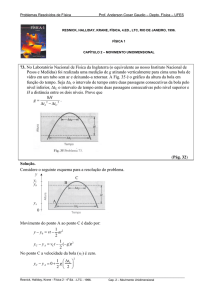
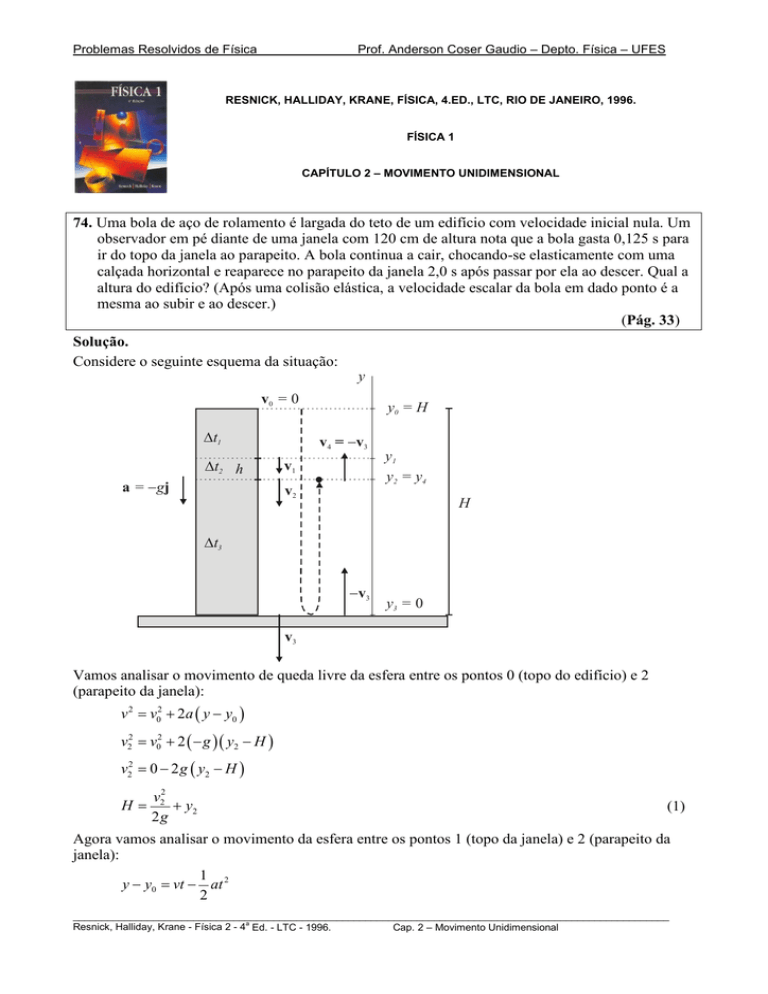
Considere o seguinte esquema da situação:
y
v0 = 0
∆t1
∆t2 h
a = −gj
y0 = H
v4 = −v3
v1
y1
y2 = y4
v2
H
∆t3
−v3
y3 = 0
v3
Vamos analisar o movimento de queda livre da esfera entre os pontos 0 (topo do edifício) e 2
(parapeito da janela):
v 2 =+
v02 2a ( y − y0 )
v22 = v02 + 2 ( − g )( y2 − H )
v22 =
0 − 2 g ( y2 − H )
=
H
v22
+ y2
2g
(1)
Agora vamos analisar o movimento da esfera entre os pontos 1 (topo da janela) e 2 (parapeito da
janela):
1
y − y0 = vt − at 2
2
________________________________________________________________________________________________________
Resnick, Halliday, Krane - Física 2 - 4a Ed. - LTC - 1996.
Cap. 2 – Movimento Unidimensional
y2 − y1 = v2 ∆t2 −
−h = v2 ∆t2 +
v2 =−
1
( − g ) ∆t22
2
1
g ∆t22
2
(1, 20 m ) − 1  9,81 m  0,125 s
h 1
− g ∆t2 =−
)
(
∆t2 2
s2 
( 0,125 s ) 2 
v2 = −10, 213125 m/s
Finalmente, vamos analisar o movimento da esfera entre os pontos 2 (parapeito da janela) e 3 (solo).
Note que o tempo requerido para a esfera ir do parapeito ao solo e retornar ao parapeito é de 2,0 s.
Logo, o tempo para ir do parapeito ao solo é de ∆t3 = 1,0 s.
1
y − y0 = v0t + at 2
2
1
y3 − y2 = v2 ∆t3 + ( − g ) ∆t32
2
1
0 − y2 = v2 ∆t3 − g ∆t32
2
1
1
m
2
2
y2=
g ∆t32 − v2 ∆t3=
 9,81 2  (1, 0 s ) − ( −10, 213125 m/s )(1, 0 s )
2
2
s 
y2 = 15,118125 m
Substituindo-se os valores de v2 e y2 em (1), teremos a resposta do problema:
=
H
( −10, 213125 m/s )
(
2 9,81 m/s 2
)
2
+ (15,118125 =
m ) 20, 434532 m
H ≈ 20 m
________________________________________________________________________________________________________
Resnick, Halliday, Krane - Física 2 - 4a Ed. - LTC - 1996.
Cap. 2 – Movimento Unidimensional
2