Problemas Resolvidos de Física

Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
RESNICK, HALLIDAY, KRANE, FÍSICA, 4.ED., LTC, RIO DE JANEIRO, 1996.
FÍSICA 1
CAPÍTULO 2 – MOVIMENTO UNIDIMENSIONAL
64. O laboratório de pesquisa da gravidade nula do Centro de Pesquisa Lewis da NASA (EUA) tem
uma torre de queda de 145 m. Trata-se de um dispositivo vertical onde se fez vácuo e que, entre
outras possibilidades, permite estudar a queda de uma esfera com diâmetro de 1 m, que contém
equipamentos. (a) Qual o tempo de queda do equipamento? Qual sua velocidade ao pé da torre?
(c) Ao pé da torre a esfera tem uma aceleração média de 25 g quando sua velocidade é reduzida
a zero. Que distância ela percorre até parar?
(Pág. 32)
Solução.
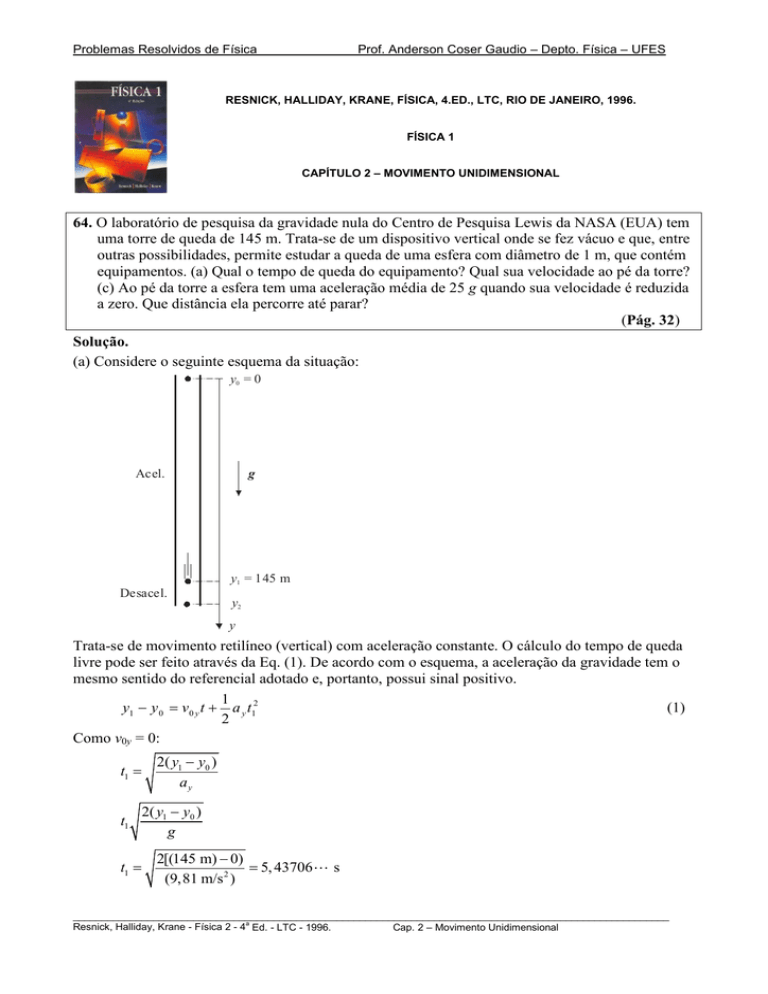
(a) Considere o seguinte esquema da situação:
y0 = 0
g
Acel.
y1 = 145 m
Desacel.
y2
y
Trata-se de movimento retilíneo (vertical) com aceleração constante. O cálculo do tempo de queda
livre pode ser feito através da Eq. (1). De acordo com o esquema, a aceleração da gravidade tem o
mesmo sentido do referencial adotado e, portanto, possui sinal positivo.
1
(1)
y1 − y 0 = v0 y t + a y t12
2
Como v0y = 0:
t1 =
t1
=
t1
2( y1 − y0 )
ay
2( y1 − y0 )
g
2[(145 m) − 0)
=
5, 43706 s
(9,81 m/s 2 )
________________________________________________________________________________________________________
Resnick, Halliday, Krane - Física 2 - 4a Ed. - LTC - 1996.
Cap. 2 – Movimento Unidimensional
t1 ≈ 5,44 s
(b) O cálculo da velocidade de chegada da esfera à base da torre também é direto.
v1 y = v0 y + a y t1
v1 y =
0 + (9,81 m/s 2 )(5, 43706 s) =
53,337604 m/s
v1 y ≈ 53,3 m/s
(c) A desaceleração ocorre entre as posições y1 e y2.
v 22 y = v12y + 2a y ( y y − y1 )
v22 y − v12y v22 y − v12y 02 − (53,337604 m/s) 2
=
∆y
=
=
= 5,8 m
2a y
2 × 25 g
2 × (25 × 9,81 m/s 2 )
∆y =
5,8 m
Obs.: O diâmetro da esfera não tem utilidade na resolução dos itens pedidos. Ele só foi dado para
ilustrar a situação.
________________________________________________________________________________________________________
Resnick, Halliday, Krane - Física 2 - 4a Ed. - LTC - 1996.
Cap. 2 – Movimento Unidimensional
2