Problemas Resolvidos de Física

Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
RESNICK, HALLIDAY, KRANE, FÍSICA, 4.ED., LTC, RIO DE JANEIRO, 1996.
FÍSICA 1
CAPÍTULO 2 – MOVIMENTO UNIDIMENSIONAL
73. No Laboratório Nacional de Física da Inglaterra (o equivalente ao nosso Instituto Nacional de
Pesos e Medidas) foi realizada uma medição de g atirando verticalmente para cima uma bola de
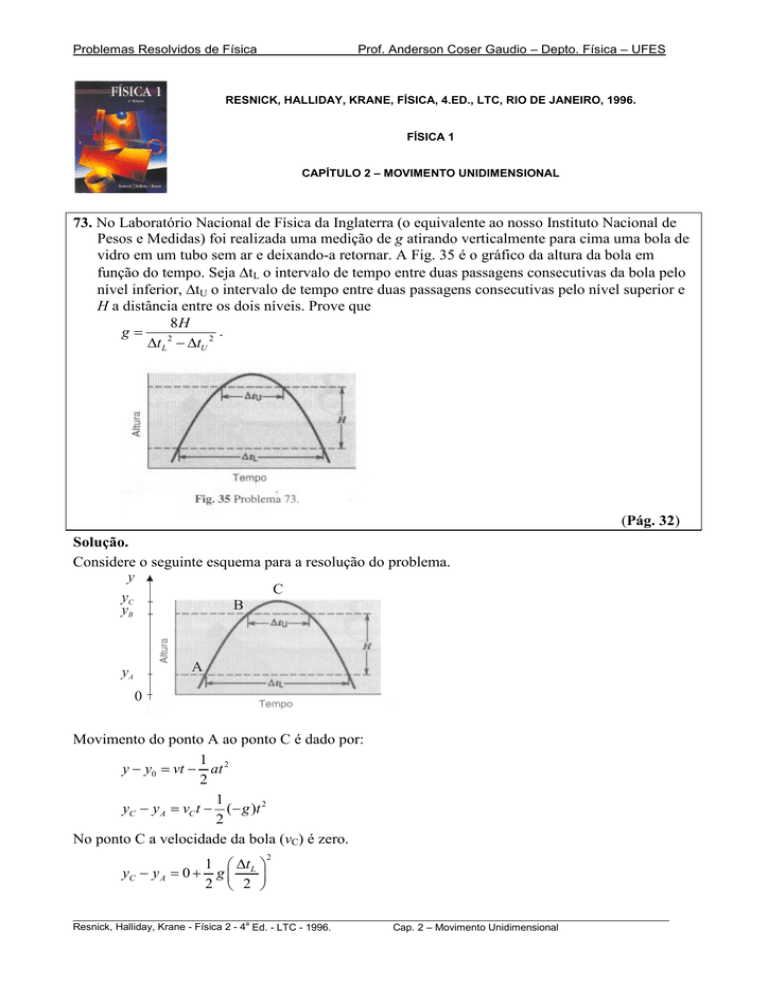
vidro em um tubo sem ar e deixando-a retornar. A Fig. 35 é o gráfico da altura da bola em
função do tempo. Seja ∆tL o intervalo de tempo entre duas passagens consecutivas da bola pelo
nível inferior, ∆tU o intervalo de tempo entre duas passagens consecutivas pelo nível superior e
H a distância entre os dois níveis. Prove que
8H
.
g=
2
∆t L − ∆tU 2
(Pág. 32)
Solução.
Considere o seguinte esquema para a resolução do problema.
y
C
yC
B
yB
A
yA
0
Movimento do ponto A ao ponto C é dado por:
1
y − y0 = vt − at 2
2
1
yC − y A = vC t − (− g )t 2
2
No ponto C a velocidade da bola (vC) é zero.
yC − y A =0 +
1  ∆t L 
g

2  2 
2
________________________________________________________________________________________________________
Resnick, Halliday, Krane - Física 2 - 4a Ed. - LTC - 1996.
Cap. 2 – Movimento Unidimensional
1
g ∆t L 2
8
De maneira idêntica, o movimento do ponto B ao ponto C é dado por:
1
yC − yB = g ∆tU 2
8
Subtraindo-se (2) de (1):
1
( yC − y A ) − ( yC − yB =
) yB − y A= H=
g (∆t L 2 − ∆tU 2 )
8
Portanto:
yC − y A =
g=
(1)
(2)
8H
∆t L − ∆tU 2
2
________________________________________________________________________________________________________
Resnick, Halliday, Krane - Física 2 - 4a Ed. - LTC - 1996.
Cap. 2 – Movimento Unidimensional
2