aula 4 - ICEB-UFOP

LABORATÓRIO DE ESTATÍSTICA - AULA 4
** Diagrama de Causa-e-Efeito e Gráfico de Pareto **
4.1 Diagrama de Causa e Efeito
“O Diagrama de Causa e Efeito é uma ferramenta utilizada para apresentar a relação existente entre
um resultado de um processo (efeito) e os fatores (causas) do processo que, por razões técnicas,
possam afetar o resultado considerado” (Werkema, 1995).
O diagrama é utilizado para sumarizar e apresentar as possíveis causas do problema considerado,
atuando como um guia para a identificação da causa fundamental deste problema e para a
determinação das medidas corretivas que deverão ser adotadas. O diagrama, por lembrar, o
esqueleto de um peixe é também denominado de Diagrama de Espinha de Peixe, ou Diagrama de
Ishikawa (em homenagem ao professor Kaoru Ishikawa1).
EXERCÍCIO 4.1 (WERKEMA, 1995, p. 97):Uma indústria automobilística verificou que, nos últimos
meses, ocorreu um aumento do número de reclamações sobre a ocorrência de defeitos no suporte
da lanterna traseira de um modelo de automóvel por ela fabricado. A empresa desejava eliminar
esta situação indesejável. Na etapa de identificação do problema, os técnicos da indústria fizeram
uma reunião com as pessoas envolvidas no processo, com o objetivo de levantar as possíveis
causas de defeito no suporte da lanterna (brainstorming). Os principais tipos de defeitos sugeridos
foram: moldagem solta, solda quebrada, centro da moldagem deslocado, lateral da moldagem
deslocada, moldagem arranhada, moldagem dentada, plástico arranhado, limpeza incompleta,
orifício deslocado e pino deslocado.
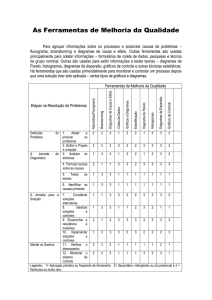
Os defeitos foram classificados, no quadro abaixo, de acordo com sua causa. Por exemplo, o defeito
Moldagem solta foi considerado como devido à Causa Humana.
1 O professor Kaoru Ishikawa construiu o primeiro diagrama de causa e efeito para explicar a alguns engenheiros de uma indústria japonesa como vários
fatores de um processo estavam interrelacionados.
b) Com os dados da planilha, construa um Diagrama de Causa e Efeito (Gráfico de Espinha de
Peixe).
Para isso, siga os passos:
4.2 Gráfico de Pareto
Este gráfico é usado nas aplicações de controle da qualidade para identificar a maioria das causas
importantes de problemas. É um gráfico de colunas arranjadas em ordem descendente de altura,
com a categoria que ocorre com maior freqüência aparecendo em primeiro lugar.
O princípio de Pareto estabelece que um problema pode ser atribuído a um pequeno número de
causas vitais. Logo, se forem identificadas as poucas causas vitais dos poucos problemas vitais
enfrentados pela empresa, será possível eliminar quase todas as perdas por meio de um pequeno
número de ações. Ou seja, em um primeiro momento, devemos concentrar nossa atenção sobre os
poucos vitais, deixando de lado os muitos triviais, para que os problemas possam ser resolvidos da
forma mais eficiente possível.
O princípio de Pareto foi inicialmente estabelecido por J. M. Juran, que adaptou aos
problemas da qualidade a teoria para modelar a distribuição de renda desenvolvida pelo
sociólogo e economista italiano Vilfredo Pareto (1843-1923). Pareto mostrou, em 1897, que
a distribuição de renda era muito desigual, com a maior parte da riqueza pertencendo a
muito poucas pessoas. Juran foi o primeiro a notar que esta mesma idéia se aplicava aos
problemas da qualidade – a distribuição dos problemas e de suas causas é desigual e,
portanto as melhorias mais significativas poderão ser obtidas se nossa atenção for
concentrada, primeiramente, na direção dos poucos problemas vitais e logo a seguir na
direção das poucas causas vitais destes problemas.
EXERCÍCIO 4.2: Voltando ao exercício 4.1. Depois de criado o Diagrama de Causa e Efeito, os
técnicos da indústria contaram o total de peças defeituosas encontradas em uma amostra de peças
produzidas durante uma semana de trabalho, de acordo com os tipos de defeito que foram
detectados. Os dados estão na tabela abaixo e se encontram no arquivo aula4ex2.mtw.
Note que nesta tabela a segunda coluna representa a freqüência de ocorrência de cada tipo de
defeito e a terceira coluna representa o prejuízo resultante da ocorrência de um defeito do tipo
correspondente (prejuízo unitário).
a) Abra o arquivo aula4ex2.mtw.
b) Crie uma coluna com os prejuízos totais correspondente a cada tipo de defeito. Para isso
siga os passos:
Responda:
b1) Qual o tipo de defeito que possui o maior prejuízo unitário? ____________
b2) Qual o tipo de defeito que possui o maior prejuízo total? ____________
c) Construa um Gráfico de Pareto onde o eixo vertical represente a quantidade de defeitos. Siga
os passos:
Responda:
c1) Você tem na coluna 1 da planilha ____ categorias de defeitos e no gráfico foram destacadas
____ categorias.
c2) Quantas categorias de defeitos foram agrupadas na coluna “outros” do gráfico? ______. A
categoria “outros” corresponde a ____ % do total de defeitos.
c3) Agrupe as categorias menos freqüentes criando uma nova categoria “outros” que englobe até
10% do total de defeitos. Para isso, siga os passos 1 a 3 do quadro acima e modifique 95 para 90
em:
No novo gráfico:
Quantas categorias de defeitos foram agrupadas na categoria “outros”? ______.
A categoria “outros” corresponde a ___ % do total de defeitos.
c4) Qual o principal defeito no suporte da lanterna? ________________. Quantas vezes este
defeito ocorreu? _____________. Este defeito corresponde a ___ % do total de defeitos.
c5) Os dois defeitos mais freqüentes contribuem com ___ % do total dos defeitos. Identifique os
tipos de defeitos que os técnicos da empresa deveriam “atacar” em primeiro lugar, com o objetivo
de melhorar os resultados que vinham sendo obtidos pela indústria. Justifique sua resposta.
______________________________________________________________________________
______________________________________________________________________________
d) Construa um Gráfico de Pareto onde o eixo vertical represente o prejuízo total associado a
cada tipo de defeito.
Siga os passos:
d1) Qual categoria de defeito responde pelo maior prejuízo total? _______________. O prejuízo
em dólares para este tipo de defeito é de ___________, que corresponde a ____ % do prejuízo
total.
d2) Quantas colunas há no gráfico? Foram aglomerados _____ categorias de prejuízo total na
categoria “outros”.
d3) Identifique os dois tipos de defeitos que os técnicos da empresa deveriam “atacar” em
primeiro lugar, com o objetivo de melhorar os resultados que vinham sendo obtidos pela indústria.
Justifique sua resposta.
________________________________________________________________________________
_______________________________________________________________________________
d4) Calcule a quantia em dólares que poderia ser economizada pela indústria, caso estes dois
defeitos fossem eliminados (obs: posicione o cursor no segundo ponto da ogiva).
EXERCÍCIO 4.3 (WERKEMA, 1995, p. 77): Uma indústria fabricante de lentes classificou uma
amostra retirada da produção de uma semana, de acordo com os tipos de defeitos detectados. Os
resultados estão abaixo.
a) Abra o arquivo aula4ex3.mtw.
b) Construa o Gráfico de Pareto onde o eixo vertical representa a quantidade de defeitos inicial
(colunas C1 e C2).
c) Identifique os dois tipos de defeitos que você "atacaria" em primeiro lugar, com o objetivo de
melhorar os resultados que vêm sendo obtidos pela indústria. Justifique a sua resposta.
________________________________________________________________________________
________________________________________________________________________________
d) Após a adoção das medidas corretivas propostas pelos funcionários, a indústria coletou uma
nova amostra, constituída de 1200 lentes, obtendo os resultados apresentados na tabela a seguir.
d1) Construa o Gráfico de Pareto onde o eixo vertical representa a quantidade de defeitos após a
implantação das melhorias (colunas C1 e C3).
d2) Quais são os dois principais problemas agora? _______________ e ___________?
Eles representam ____% do total de defeitos.
e) Calcule a Melhoria Total usando a seguinte fórmula:
4.3 Desdobramento de Gráficos de Pareto
O desdobramento de gráficos de Pareto consiste em tomar as categorias identificadas como
prioritárias (“poucos vitais”) em um primeiro gráfico como novos problemas a serem analisados por
meio de novos gráficos de Pareto. O desdobramento continua até que o nível de detalhamento
desejado seja obtido.
EXERCÍCIO 4.4: (WERKEMA,1995 p. 94). Uma indústria automobilística registrou a ocorrência de
161 defeitos em automóveis de um certo modelo. Os dados da tabela abaixo e os desdobramentos
dos dois principais defeitos estão no projeto do Minitab projAula4ex4.mpj.
a) Abra o arquivo:
b) Construa os gráficos de Pareto para as tabelas acima. Selecione, usando o menu Window, cada
uma das pastas de trabalho (worksheets)
b1) Abra a planilha “defeitos nos automóveis”, construa o gráfico de Pareto e responda:
Os defeitos mais frequentes são: ______________ e ______________. Eles respondem por ____ e
____% dos defeitos respectivamente. Juntos respondem por ___% dos defeitos.
b2) Abra a planilha “defeitos na carroceria”, construa o gráfico de Pareto e responda:
Os defeitos mais frequentes são: ______________ e ______________. Eles respondem por ____ e
____% dos defeitos respectivamente. Juntos respondem por ___% dos defeitos.
b3) Abra a planilha “defeitos na pintura” , construa o gráfico de Pareto e responda:
A categoria arranhão corresponde a ____% dos defeitos na pintura.
b4) Abra a planilha “defeitos nos acessórios”, construa o gráfico de Pareto e responda:
Os defeitos no ar condicionado respondem por ____% dos defeitos nos acessórios
b5) Abra a planilha “defeitos no ar condicionado”, construa o gráfico de Pareto e responda:
O que mais causa reclamação é que o ar não funciona, correspondendo a ____% das reclamações.
4.4 Estratificação de Gráficos de Pareto
A comparação de gráficos de Pareto construídos considerando diferentes níveis de fatores de
estratificação de interesse pode ser muito útil para a identificação das causas fundamentais de um
problema. A estratificação consiste agrupar os dados de acordo com fatores de forma a possibilitar
uma melhor avaliação do problema. Os fatores de estratificação usuais são: região, turno, tempo
(dia, semana,mês), operador, lote de matéria prima e máquina (tipo, fabricante).
EXERCÍCIO 4.5: Uma companhia de seguros colocou como meta reduzir a ocorrências de erros no
preenchimento de formulários de apólice de seguro. Nesta empresa, existiam dois modelos distintos
de formulários (I e II), quatro operadores (Júnia, Júlia, Jorge e José) trabalhavam no preenchimento
das apólices e cinco tipos de erros (A, B, C , D e E) poderiam ocorrer. Durante uma semana de
trabalho foram registrados 557 erros de preenchimentos nos formulários. Os dados estão digitados
no arquivo aula4ex5.mtw. (adaptado de WERKEMA,1995, p. 100).
a) Construa um gráfico de Pareto para os Tipos de erro;
Observação: Note que estamos trabalhando com os dados brutos, ou seja, cada linha do
arquivo corresponde a um erro de preenchimento do formulário. Por isto é que usamos
“Chart defects data in” em vez de “Chart defects table”. Este último é usado quando já
temos uma tabela já pronta com os tipo de erros e a freqüência de cada um.
b) Repetir os passos do item a) para Operador, Dia da semana e Formulário. Quais são as suas
conclusões?
Complete:
O tipo de erro mais freqüente no preenchimento das apólices é o tipo ____, que corresponde a
_____ %
do total de erros. O operador que mais comete erros é __________, que responde por ___% do total
de erros dos operadores. O dia da semana não é um causador de problemas, pois a Quinta, a
Terça, a Quarta, a Sexta e a Segunda feira respondem por _____, _____, _____, _____e _____%
dos erros, respectivamente. Também não há grande diferença entre a quantidade de erros nos dois
tipos de formulário, onde o formulário I responde por ___%dos preenchidos com erro e o do tipo II
com o restante.
c) Construa um gráfico de Pareto para os tipos de erros considerando: Operador, Dia da semana e
Formulário. Analise os resultados.
Siga os passos:
Bibliografia
WERKEMA, M. C. C. As ferramentas básicas para o gerenciamento de processos. Belo Horizonte:
UFMG: Fundação Christiano Ottoni, 1995 (Ferramentas da Qualidade, 2). cap 4 e 5.