2ª Lista de Exercícios de Física I (Movimento em Uma Dimensão

D EPARTAMENTO DE M ATEMÁTICA
C AMPUS U NIVERSITÁRIO DE S INOP
U NIVERSIDADE DO E STADO DE M ATO G ROSSO
2ª Lista de Exercícios de Física I
(Movimento em Uma Dimensão)
1. Um motorista dirige para o norte por 35,0 min a 85 km/h e então para por 15,0 min. Em seguida
continua para o norte, viajando 130 km em 2,00 h.
(a) Faça o gráfico das posições x em quilômetros versus o tempo t em horas, lembrando que o
instante inicial pode ser considerado t = 0 s e o instante final é t = 35,0 min + 15,0 min +
2,00 h = 170 min = 10 200 s ' 2,83 h
(b) Qual é seu deslocamento total?
(c) Qual é a sua velocidade média neste percurso?
2. A posição de um objeto que se move ao longo de um eixo x é dada por x (t) = 2t − 3t2 , em que
x está em metros e t em segundos.
(a)
(b)
(c)
(d)
Faça o gráfico de x versus t para 0 ≤ t ≤ t = 4 s.
Qual o deslocamento do objeto entre t = 2 s e t = 4 s?
Qual a velocidade média para o intervalo de tempo t = 1 s a t = 4 s?
Qual a função velocidade v(t) e aceleração a(t)?
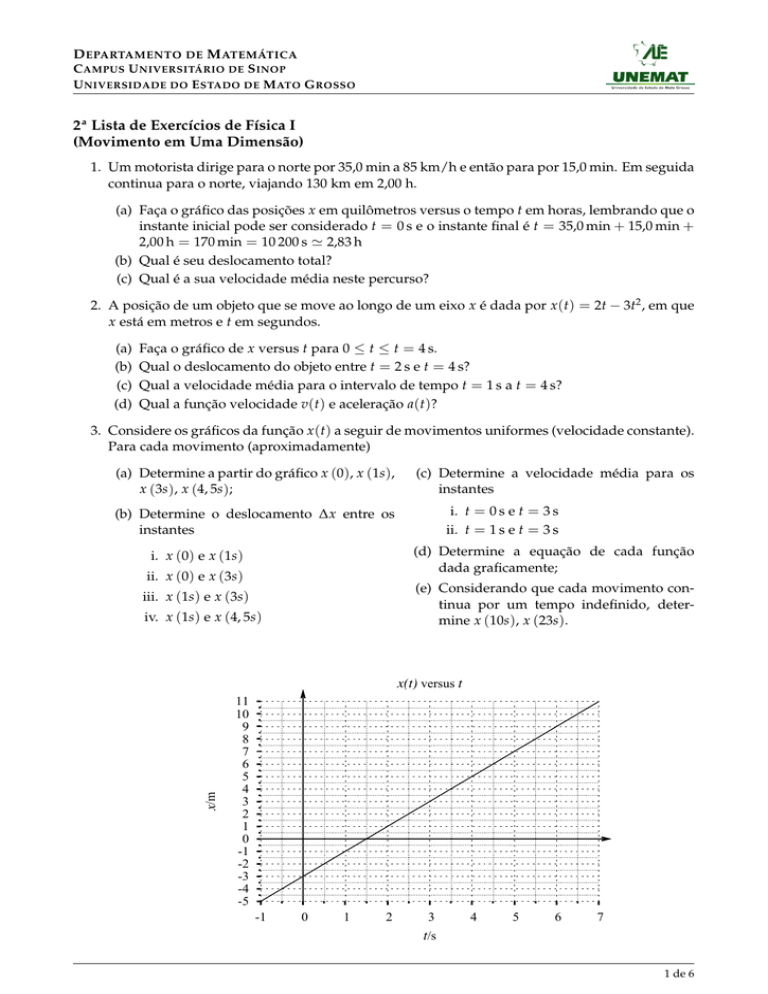
3. Considere os gráficos da função x (t) a seguir de movimentos uniformes (velocidade constante).
Para cada movimento (aproximadamente)
(a) Determine a partir do gráfico x (0), x (1s),
x (3s), x (4, 5s);
(c) Determine a velocidade média para os
instantes
(b) Determine o deslocamento ∆x entre os
instantes
i. t = 0 s e t = 3 s
ii. t = 1 s e t = 3 s
(d) Determine a equação de cada função
dada graficamente;
i. x (0) e x (1s)
ii. x (0) e x (3s)
(e) Considerando que cada movimento continua por um tempo indefinido, determine x (10s), x (23s).
iii. x (1s) e x (3s)
iv. x (1s) e x (4, 5s)
x/m
x(t) versus t
11
10
9
8
7
6
5
4
3
2
1
0
-1
-2
-3
-4
-5
-1
0
1
2
3
4
5
6
7
t/s
1 de 6
D EPARTAMENTO DE M ATEMÁTICA
C AMPUS U NIVERSITÁRIO DE S INOP
U NIVERSIDADE DO E STADO DE M ATO G ROSSO
x(t) versus t
0
x/m
-5
-10
-15
-20
-1
0
1
2
3
4
5
6
7
t/s
4. Considere os gráficos da função x (t) a seguir de movimentos uniformemente variados (aceleração constante). Para cada movimento (aproximadamente)
(a) Determine a partir do gráfico x (0), x (1s),
x (3s), x (4, 5s);
(c) Determine a velocidade média para os
instantes
(b) Determine o deslocamento ∆x entre as
posições
i. t = 0 s e t = 3 s
ii. t = 1 s e t = 3 s
(d) Determine a equação de cada função
dada graficamente;
i. x (0) e x (1s)
ii. x (0) e x (3s)
(e) Considerando que cada movimento continua por um tempo indefinido, determine x (10s), x (20s).
iii. x (1s) e x (3s)
iv. x (1s) e x (4, 5s)
x(t) versus t
70
60
50
x/m
40
30
20
10
0
-10
-1
0
1
2
3
4
5
6
t/s
2 de 6
D EPARTAMENTO DE M ATEMÁTICA
C AMPUS U NIVERSITÁRIO DE S INOP
U NIVERSIDADE DO E STADO DE M ATO G ROSSO
x(t) versus t
25
20
15
10
x/m
5
0
-5
-10
-15
-20
-25
-1
-0.5
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
t/s
5. Considere os gráficos da função x (t) a seguir de movimentos . Para cada movimento (aproximadamente)
iii. t = 1 s e t = 3 s
iv. t = 1 s e t = 4,5 s
(a) Determine a partir do gráfico x (0), x (1s),
x (3s), x (4, 5s);
(b) Determine o deslocamento ∆x entre os
instantes
(c) Determine a velocidade média para os
instantes
i. t = 0 s e t = 1 s
ii. t = 0 s e t = 3 s
i. t = 0 s e t = 3 s
ii. t = 1 s e t = 3 s
x(t) versus t
-1
-2
x/m
-3
-4
-5
-6
-1
-0.5
0
0.5
1
1.5
2
t/s
3 de 6
D EPARTAMENTO DE M ATEMÁTICA
C AMPUS U NIVERSITÁRIO DE S INOP
U NIVERSIDADE DO E STADO DE M ATO G ROSSO
x(t) versus t
400
350
300
x/m
250
200
150
100
50
0
-50
-1
-0.5
0
0.5
1
1.5
2
2.5
3
3.5
6
7
8
t/s
x(t) versus t
5
4
3
2
x/m
1
0
-1
-2
-3
-4
-5
-1
0
1
2
3
4
5
t/s
6. A distância mínima para necessária para parar um carro em movimento a 60,0 km/h é de 40
m. Qual é a distância mínima para parar o mesmo carro em movimento a 140 km/h, supondo
a mesma taxa de aceleração?
7. Um rojão de fogos de artifício atira para cima na direção vertical uma carga de explosivos com
uma velocidade inicial de 35,0 m/s. O bocal do rojão está colocado a 1,00 m acima do do chão,
de onde sai a carga de explosivos.
(a) Quais são as equações de posição (altura) e velocidade (velocidade vertical) que descrevem o movimento da carga de explosivos?
(b) Quanto tempo deve demorar para estourar a carga de explosivos para que ela detone no
ponto mais alto possível? Considere que a carga de explosivos é ativada na saída do bocal
do rojão.
(c) Faça o gráfico de x versus t para 0 ≤ t ≤ tmax .
4 de 6
D EPARTAMENTO DE M ATEMÁTICA
C AMPUS U NIVERSITÁRIO DE S INOP
U NIVERSIDADE DO E STADO DE M ATO G ROSSO
8. Uma bola é arremessada diretamente para baixo com uma velocidade inicial de 8,00 m/s de
uma altura de 30,0 m.
(a) A bola atinge o solo após qual intervalo de tempo?
(b) Faça o gráfico de y versus t para 0 ≤ t ≤ tmax .
9. Em um canteiro de obras uma chave de cano bate no chão com uma velocidade de de 24 m/s.
(c) Faça o gráfico de y versus t para 0 ≤ t ≤
tmax .
(a) De que altura deixaram-na cair?
(b) Quanto tempo durou a queda?
10. Uma superbola de 50,0 g com uma velocidade de 25,0 m/s colide com uma parede de tijolos e
volta com uma velocidade de 22,0 m/s. Se a bola permanece m contato com a parede durante
3,50 ms, qual é o módulo da aceleração média da bola durante este intervalo de tempo?
11. Considere os gráficos da função v(t) a seguir de movimentos de dois carros que variam suas
velocidades. Para cada movimento (aproximadamente)
(a) Determine a partir do gráfico v (0), v (1s),
v (5s), v (6, 5s);
(b) Determine o deslocamento ∆x entre os
instantes
i. t = 0 s e t = 2 s
ii. t = 2 s e t = 4 s
iii. t = 4 s e t = 6 s
iv. t = 0 s e t = 6 s
(c) Determine a aceleração média para os
instantes
i. t = 0 s e t = 3 s
ii. t = 1 s e t = 3 s
(d) Determine as funções v(t)
v(t) versus t
10
5
v/m
0
-5
-10
-15
-20
-1
0
1
2
3
4
5
6
7
t/s
5 de 6
D EPARTAMENTO DE M ATEMÁTICA
C AMPUS U NIVERSITÁRIO DE S INOP
U NIVERSIDADE DO E STADO DE M ATO G ROSSO
v(t) versus t
20
15
v/m
10
5
0
-5
-10
-1
0
1
2
3
4
5
6
7
t/s
Cinemática unidimensional: posição, desloca- Equações do MU: Movimento Uniforme
mentos, velocidades e acelerações
s ( t ) = s0 + v0 t
v ( t ) = v0
s = s ( t ),
∆s = s (t2 ) − s (t1 ) ,
s ( t2 ) − s ( t1 )
t2 − t1
v ( t2 ) − v ( t1 )
amed (t1 , t2 ) =
t2 − t1
ds
v(t) = ,
dt
dv
a(t) =
dt
vmed (t1 , t2 ) =
(6)
(7)
(1)
(2)
(3)
(4)
(5)
Equações do MUV: Movimento Uniformemente
Variado
a
s ( t ) = s0 + v0 t + t2
2
v(t) = v0 + at
2
v =
v20
+ 2a (s − s0 )
(8)
(9)
(10)
com s0 ≡ s (t0 ) e v0 ≡ v (t0 ), sendo t0 = 0 s.
6 de 6