Solução da prova da 1ª Fase
2016 – Nível 2
SOLUÇÕES 1ª FASE 2016OBMEP
N2
1
QUESTÃO 1
ALTERNATIVA B
QUESTÃO 1
ALTERNATIVA B
Cada faixa da bandeira tem área igual a 300 cm2. As partes brancas da faixa
superior têm, portanto, área igual a 150 cm2. A parte branca da faixa do meio tem área
2
2
2 igual a 150 cm2.
Cada faixa da bandeira tem
área
igualcm
a 300
. As partes
brancas
faixainferior
superior
têm,
portanto,
área
igual
a 100
e cm
as partes
brancas
dada
faixa
têm
área
120 cm
. Logo, a soma
2
A parte branca da faixa do
meio
tem
área
igual
a
100
cm
e
as
partes
brancas
da
faixa
inferior
têm
área
120 cm2. Logo, a
das áreas dos retângulos brancos é 150 + 100
2
soma das áreas dos retângulos
+ 120 =brancos
370 cmé2150
. + 100 + 120 = 370 cm .
Em outras palavras, se A1, A 2 e A3 são as áreas dos retângulos brancos,
Em
outras
palavras,
sealgarismos
A1, aA2área
e éAtotal
asdividirmos
áreas 999 por 13, temos como
3 são
respectivamente, em cada
uma
das
três
faixas,
de
O maior
número
de trêsentão,
999.
Se todos
2 cada uma
dos
retângulos
respectivamente
em
os retângulos brancos
é A176+ eAresto
+ A311.
= 150
100–+11120
= 370
. múltiplo de 13 com três algarismos e a
resultado
Logo+999
= 988
é o cm
maior
2
faixas,
área total de todos os
soma dedas
seus três
algarismos
é 9então,
+ 8 + 8 =a25.
retângulos brancos é A1 + A2 + A3 = 150 + 100 +
QUESTÃO 2 QUESTÃO
6
2
ALTERNATIVA
B cm .
ALTERNATIVA
B 120 = 370
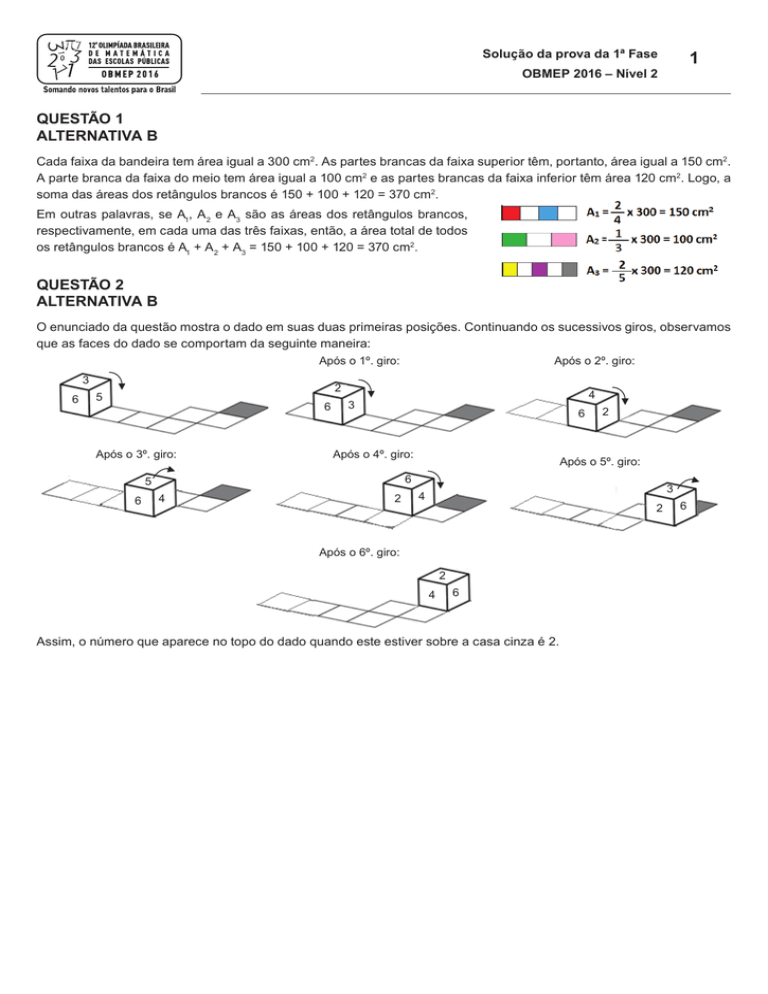
O enunciado da questão mostra o dado em suas duas primeiras posições. Continuando
QUESTÃO
2 em suas
O enunciado da questão
mostra
o dado
duas
primeiras
posições.
Continuando
os sucessivos
os sucessivos
giros,
observamos
que
as faces
do dado
se comportam
da seguinte
maneira: giros, observamos
ALTERNATIVA
B
que as faces do dado se comportam da seguinte
maneira:
N1Q6
3
6
QUESTÃO 3
ALTERNATIVA A
5
N1Q9
Após o 1º. giro:
2
6
Após o 3º. giro: QUESTÃO 4
ALTERNATIVA D
5
6
Após o 2º. giro:
4
3
6
Após o 4º. giro:
2
Após o 5º. giro:
6
Como quatro alunos correspondem
a 10% dos alunos da escolinha de futebol,
3
4
= 40 alunos. Logo, 40 – 4 = 36 alunos
4 concluímos que esta tem 4 ÷ (10/100)
2
2 6
participam somente da escolinha de futebol. Os mesmos quatro alunos correspondem
a 25% dos alunos da escolinha de basquete que tem, portanto, 4 ÷ (25/100) = 16
alunos. Assim, 16 – 4 =Após
12 alunos
o 6º. giro:participam somente desta escolinha.
2
Conclusão: o número de atletas que participam
somente de uma escolinha é 36 + 12 =
4 6
48.
QUESTÃO 5
ALTERNATIVA
Assim, o número que aparece
no topo doBdado quando este estiver sobre a casa cinza é 2.
Assim, o número Observe
que aparece
o topo
dado
estiver sobre
que
AB,doAC
e quando
BC sãoeste
diagonais
dasa casa cinza é 2.
o
60
faces do cubo e, portanto, possuem a mesma medida.
QUESTÃO 7
Logo, os
ALTERNATIVA
E segmentos AB e AC são lados do triângulo
equilátero
O com
ângulo
é, éentão,
ângulocartela acrescida dos
Observe
que ABC.
a cartela
seis BÂC
adesivos
idênticaum
à primeira
adesivosinterno
e de
. Logo,
o
preço
da
cartela
com
seis
adesivos
é
um triângulo equilátero, que mede 60º.igual a 16 reais mais o preço
desses dois adesivos. Por outro lado, esses dois adesivos aparecem na segunda cartela
juntamente com os adesivos
e
, mas esses dois últimos adesivos juntos custam 5 reais,
QUESTÃO 6
como mostra a terceira cartela. Logo o preço dos adesivos
e , juntos, é 12 – 5 = 7 reais e,
ALTERNATIVA
C com seis adesivos custa 16 + 7 = 23 reais.
como conseqüência,
a cartela
Vamos colocar todos os gabaritos em uma mesma tabela, usando as letras A,
Beatriz e Cecília, respectivamente.
Observe B
uma
da solução:
e Cvariação
para denotar
Ana,
1
2 3 4
5
A ABC A C BC
B
BC
AC
C
B
Ou seja,
Portanto, o preço da cartela com 6 adesivos é igual a 16 + 12 – 5 = 23 reais.
a nossa
escolha,
dentreno
os intervalo
númerosacima,
no intervalo
acima, aos
números
pares
reduz a nossareduz
escolha,
dentre
os números
aos números
pares
que vão
do 6que vão do 6
ao 48.
agora
que,que,
alémalém
disso,
queremos
cujascujas
metades
sejam
números
ao 48.
Considerando
agora
que,queremos
além números
disso,
queremos
números
cujas
metades
sejam números
ao Considerando
48. Considerando
agora
disso,
números
metades
sejam
números
de dois
algarismos,
nossa
escolha
fica
restrita
aos
números
pares
entre
20
e
48,
incluindo
o
20
de doisnossa
algarismos,
nossa
escolhaaos
ficanúmeros
restrita aos
números
pares
20 e 48,
de dois algarismos,
escolha
fica restrita
pares
entre 20
e 48,entre
incluindo
o 20incluindo o 20
e o 48.
sem sem
listá-los,
observando,
por exemplo,
quepor
econtá-los
o 48.
Podemos
contá-los
sem
listá-los,
observando,
e oPodemos
48. Podemos
contá-los
listá-los,
observando,
por
exemplo,
queexemplo, que
Solução da prova da 1ª Fase
2
20 =20
2 x=10,
22
=
2
x
11,
24
=
2
x
12,.......,
48
2x x12,.......,
24
24 ==248
= 2–xNível
24 2
2 x 10, 20
22==22x x10,
11, 22
24==22xx11,
12,.......,
=OBMEP
2 x 24 48
2016
e teremos
24 –24
10e–+teremos
1 =+ 15
satisfazem
asque
condições
do enunciado
. do
24
10 +que
1 = que
15 números
as
e teremos
10
1 =números
15–números
satisfazem
assatisfazem
condições
docondições
enunciado
. enunciado.
QUESTÃO
3
QUESTÃO
9 9 QUESTÃO 9
QUESTÃO
ALTERNATIVA
AALTERNATIVA
ALTERNATIVA
A
A
ALTERNATIVA
A
Iniciamos
observando
que que
Joãozinho fez
4fez
furos
na folha
desdobrada,
umadesdobrada,
vez vez
que queuma vez que
Iniciamos
observando
que
Joãozinho
fez 4
furos
na folha
Iniciamos
observando
4 furos
na
desdobrada,
uma
Iniciamos observando
que
Joãozinho
fez 4escolhido
furos na Joãozinho
folha
desdobrada,
uma
vezfolha
que,
após
asAduas
dobras,
o local escolhido
apósapós
as duas
dobras,
o
local
para
furar
tem
4
camadas
de
papel.
figura
abaixo
as duas
dobras,
o local
escolhido
para
furar tem de
4 camadas
de papel.
A figura abaixo
as duasapós
dobras,
o local
escolhido
para
furar tem
4 camadas
papel. A figura
abaixo
mostra
a
posição
dos
furos
após
cada
desdobra.
Observamos
ainda
que,
após
uma
desdobra,
para furar tem
4
camadas
de
papel.
A
figura
abaixo
mostra
a
posição
dos
furos
após
cada
desdobra.
Observamos
ainda
mostra
posição
doscada
furos
após cada
desdobra. Observamos
ainda
que,
após uma desdobra,
mostra a posição
dosa furos
após
desdobra.
Observamos
ainda que, após
uma
desdobra,
para
cada
furo
obtemos
dois:
um
na
mesma
posição
e
outro
em
posição
simétrica
à
linha
de
que, após umapara
desdobra,
para
cada
obtemos
nanamesma
posição
posição
dede
para
cadafuro,
furo
obtemos
dois:um
umposição
mesma
posição
eoutro
outroem
em
posição
simétrica
à linha
cada furo
obtemos
dois:
um nadois:
mesma
e outro
em eposição
simétrica
àsimétrica
linha
de à linha
desdobra.
desdobra. desdobra.
desdobra.
Dentre
as figuras
das alternativas,
aessas
primeira
respeita
simetrias.
Dentre
figuras apenas
das apenas
alternativas,
apenas
a essas
primeira
respeita
essas simetrias.
Dentre
as figuras
das
alternativas,
a primeira
respeita
essas
simetrias.
Dentre as figuras das
alternativas,
apenas
aasprimeira
respeita
simetrias.
Vejamos
com com
mais
detalhes:
folha
desdobrada,
notamos
Vejamos
comnamais
na folha
desdobrada,
notamos
Vejamos
mais
detalhes:
na detalhes:
folha
desdobrada,
notamos
que
os
vincos
deixados
pelas
duas
dobras
feitas
têm
o
Segundo
Vejamos com mais
nadeixados
folha
desdobrada,
notamos
osdobras
vincos
deixados
pelas
duas
que
os vincos
deixados
pelas que
duas
têm
o
seguinte
que detalhes:
os vincos
pelas
duas
dobras
feitas
têmseguinte
o feitas
seguinte
vincoSegundo
aspecto:
vinco
aspecto:
aspecto:
dobras feitas têm o seguinte aspecto:
Há dois
furosfuros
inferiores
com com
relação
ao primeiro
Há
doissimétricos
furos
inferiores
simétricos
com
relação ao Primeiro
primeiro
Há dois
inferiores
simétricos
relação
ao primeiro
vinco
e
mais
dois
furos
superiores
que
aparecem
quando
Primeiro
vinco
Há dois furos inferiores
commais
relação
ao furos
primeiro
vinco
e mais
dois
furos superiores
vincodois
e
dois
superiores
que
aparecem
quando
vinco e simétricos
mais
furos
superiores
que
aparecem
quando
vinco
desdobramos
a
última
dobra;
esses
furos
superiores
são
simétricos
desdobramos
a última
dobra;
esses
superiores
são simétricos
que aparecem desdobramos
quando desdobramos
última
dobra;
esses
furos furos
superiores
são simétricos
aos
a última adobra;
esses
furos
superiores
são
simétricos
aos inferiores
comaos
relação
ao segundo
vinco.
inferiores
com
relação
ao segundo vinco.
inferiores
com
relação
segundo
vinco.
inferiores com aos
relação
ao segundo
vinco. ao
Simétricos com
Simétricos com
relação ao primeiro
relação ao primeiro
vinco
vinco
Segundo
vinco
Primeiro
vinco
Simétricos com
relação ao primeiro
vinco
Simétricos com
Simétricos com
Simétricos com
relação ao segundo
relação ao segundo relação ao segundo
vinco
vinco
vinco
Simétricos com
Simétricos com
Simétricos com
relação ao segundo
relação ao segundo relação ao segundo
vinco
vinco
vinco
Simétricos com
Simétricos com
relação ao primeiro
relação ao primeiro
vinco
vinco
Simétricos com
relação ao primeiro
vinco
QUESTÃO
10 10
QUESTÃO 10
QUESTÃO
4QUESTÃO
ALTERNATIVA
BALTERNATIVA
B
ALTERNATIVA
B
ALTERNATIVA
D
A diferença entre o maior e o menor palpite é 274 – 234 = 40 e 40 pode ser escrito como 40 =
A diferença
o maior
e o menor
274e –40234
= 40
40 pode
ser escrito
A diferença entre
o maiorentre
e o menor
palpite
é 274palpite
– 234 =é 40
pode
sere escrito
como
40 = como 40 =
31 +31
9.
Isto
leva
igualdades:
274 274
–igualdades:
31
234
+ 274
9 =+ 243.
queque
Como quatro
alunos
correspondem
a 10%
dos
alunos
da–=31
escolinha
futebol,
tem
31 leva
+às9.seguintes
Isto
nos
leva
às
seguintes
–9de
31
=Podemos
234Podemos
+ 9concluímos
=concluir
243.
Podemos
concluir
que
+
9. nos
Isto
nos
às seguintes
igualdades:
= 234
= 243.
concluir
que esta
4 x 10 = 4 ÷ (10/100) = 4 ÷ (1/10) = 40 alunos. Logo, 40 – 4 = 36 alunos participam somente da escolinha de
futebol. Os mesmos quatro alunos correspondem a 25% dos alunos da escolinha de basquete, que tem, portanto,
4 x 4 = 4 ÷ (25/100) = 4 ÷ (1/4) = 16 alunos. Assim, 16 – 4 = 12 alunos participam somente dessa escolinha.
Conclusão: o número de atletas que participam somente de uma escolinha é 36 + 12 = 48. QUESTÃO 5
ALTERNATIVA B
Observe que AB, AC e BC são diagonais das faces do cubo e, portanto, possuem
a mesma medida. Logo, os segmentos AB e AC são lados do triângulo equilátero
ABC. O ângulo BÂC é, então, um ângulo interno de um triângulo equilátero, que
mede 60º.
Solução da prova da 1ª Fase
OBMEP 2016 – Nível 2
QUESTÃO 6
ALTERNATIVA C
D
3
A
Vamos colocar todas as respostas, identificandoEsuas respectivasAautoras, em
B uma mesma tabela.
A
B
1
Ana, Beatriz e
Cecília
C
2
3
Ana
Beatriz e
Cecília
Cecília
4
Beatriz e
Cecília
5
Ana e Cecília
Beatriz
A prova tem cinco questões; como Ana acertou quatro questões e Cecília três,
D concluímos que elas devem ter acertado pelo menos duas
Ana
questões em comum, e a
questões 1 e 5. Mas Beatriz também
acertou
E tabela nos mostra que elas acertaram asAna
Beatriz
a questão 1, logo errou todas as outras; concluímos que Cecília não acertou as
A prova tem cinco questões. Como Ana acertou quatro questões e Cecília três, concluímos que elas devem ter acertado
questões 2 e 4, e logo ela acertou também a questão 3. Segue que Ana errou a
pelo menos duas questões em comum, e a tabela nos mostra que elas acertaram as questões 1 e 5. Mas Beatriz também
questão 3.
acertou a questão 1; logo, errou todas as outras. Concluímos que Cecília não acertou as questões 2 e 4, e, logo, ela
acertou tambémQUESTÃO
a questão 73. Segue que Ana errou a questão 3.
ALTERNATIVA A
Se Jurema pintar a sequência de 13 quadradinhos iniciando com o
QUESTÃO 7
quadradinho
da extremidade esquerda e depois pintar outra sequência terminando no
ALTERNATIVA A
quadradinho da extremidade direita, nesses dois casos, ela obrigatoriamente deverá
Se Jurema pintar
a sequência
de 13 quadradinhos
iniciando
com o quadradinho
da extremidade
pintar
pintar
nove quadradinhos,
a saber,
os quadradinhos
que vão
de 5 a 13,esquerda
incluindoe depois
os
outra sequênciaextremos.
terminandoEsses
no quadradinho
da
extremidade
direita,
nesses
dois
casos,
ela
obrigatoriamente
deverá
pintar
mesmos quadradinhos serão também pintados se ela começar a
nove quadradinhos,
a
saber,
os
quadradinhos
que vão de 5 ao 13,
incluindo
os extremos.
Esses
mesmos
pintar a partir do segundo quadradinho,
mesmo
também
ocorrerá
se ela
iniciarquadradinhos
a
serão também pintar
pintados
se
ela
começar
a
pintar
a
partir
do
segundo
quadradinho;
o
mesmo
também
a partir do terceiro ou do quarto quadradinho. Logo, os nove quadradinhos,ocorrerá
que se ela
iniciar a pintar avão
partir
do quarto quadradinho.
Logo, os nove quadradinhos,
do 5 ao 13,
serão
dodo5terceiro
ao 13,ouincluindo-os,
serão obrigatoriamente
pintados, qualquer
queincluindo-os,
seja a
obrigatoriamente pintados, qualquer que seja a escolha de Jurema.
escolha de Jurema.
QUESTÃO 8
QUESTÃO 8 ALTERNATIVA D
ALTERNATIVA
D
N1Q14
A tabela abaixo indica o que João e Maria dizem a respeito do dia da brincadeira (hoje, no diálogo) em cada pergunta:
QUESTÃO 9
Pergunta
João
Maria
ALTERNATIVA D
Como João e Maria partem
do mesmo quinta
ponto da pista
e em sentidos contrários, mantendo
Primeira
sexta
constantes suas respectivas velocidades, no momento em que João tiver corrido 1200 metros
Segunda
domingo
sábado
da pista, Maria terá corrido 3000 – 1200 = 1800 metros da mesma (quando ambos se
Terceira
quarta Joãoquinta
encontram pela primeira vez).
Assim, enquanto
corre 1200 metros, Maria corre 1800.
Portanto, quando João correr 3000 metros nessa pista,
Como, pelo enunciado, João e Maria deram a resposta correta exatamente uma vez, concluímos que a brincadeira
Maria terá corrido (3000 x 1800) ÷ 1200 = 4500 metros.
aconteceu em uma quinta-feira.
3000
Outra solução: Observamos
a resposta
correta de
foi para
a primeira
Uma maneiraque
simples
de visualizar
a João
solução
consiste
em pergunta “Que dia da semana é hoje?”. As
600
outras duas respostas
João em
não cinco
podemtrechos
ser verdadeiras,
pois implicariam
dividir adepista
de 600 metros
cada e que todas as respostas de Maria estariam
600ou seja, se
erradas. De fato,
se
a
resposta
correta
de
João
fosse
para
a
pergunta
“Que dia da semana 2400
será amanhã?”,
acompanhar os movimentos de João e Maria. Enquanto
o dia seguinte fosse
uma dois
segunda-feira,
a conversa
teria três.
ocorrido em um domingo e o dia anterior seria um sábado,
João corre
desses trechos,
Maria corre
1800
2400
confirmando que as três respostas de Maria estariam erradas. Conclusão análoga é encontrada1200
se a resposta correta de
João fosse para a pergunta “Que dia da semana foi ontem?”. Portanto, a conversa ocorreu em uma quinta-feira.
1200
1800
QUESTÃO 8
ALTERNATIVA D
N1Q14
Solução da prova da 1ª Fase
OBMEP 2016 – Nível 2
4
QUESTÃO 9
QUESTÃO 9
ALTERNATIVA D
ALTERNATIVA DComo João e Maria partem do mesmo ponto da pista e em sentidos contrários, mantendo
constantes suas respectivas velocidades, no momento em que João tiver corrido 1200 metros
Como João e Maria partem do mesmo ponto da pista e em sentidos contrários, mantendo constantes suas respectivas
da pista, Maria terá corrido 3000 – 1200 = 1800 metros da mesma (quando ambos se
velocidades, no momento
em que
João
tiver corrido
1200 metros
da pista,
corrido
3000
– 1200
= 1800
metros
encontram
pela
primeira
vez). Assim,
enquanto
JoãoMaria
correterá
1200
metros,
Maria
corre
1800.
da mesma (quando Portanto,
ambos se encontram
pelacorrer
primeira
vez).metros
Assim, nessa
enquanto
João corre 1200 metros, Maria corre 1800.
quando João
3000
pista,
Portanto,Outra
quando
João
correr
3000
metros
nessa
pista,
Maria
terá
corrido
(3000
Maria
terá corridode(3000
1200
= 4500
solução:
a velocidade
Mariax é1800)
3/2 =÷1,5
vezes
a demetros.
João, já que ele corre 1200 metros
x 1800) ÷
= 4500
metros.
no1200
mesmo
tempo
que ela corre 1800 metros. Logo, enquanto este corre 3000 metros, ela corre
3000
maneira
deconsiste
visualizar
solução
consiste
1,5 x 3simples
000Outra
=Uma
4500
metros.asimples
Uma maneira
de solução:
visualizar
avelocidade
solução
eméadividir
a pista
emacinco
de
Maria
3/2
= 1,5
vezes
deem
João, já que 600
ele corre 1200 metros
a a
pista
em
trechos
de
600
metros
trechos de 600
metros
cada
evelocidade
acompanhar
os
movimentos
de
Joãoaenquanto
edecada
Maria.
Outra
solução:
decorre
Maria
é 3/2
= 1,5
vezes
João,eeste
já que
ele 3000
corre metros,
1200 metros
nodividir
mesmo
tempo
que cinco
ela
1800
metros.
Logo,
corre
ela corre
600
2400
acompanhar
os
movimentos
de
João
e
Maria.
Enquanto
Enquanto Joãonocorre
desses
trechos,
Maria
corre
três. Logo, enquanto este corre 3000 metros,
mesmo
tempo
que
ela
corre
1800
metros.
ela corre
1,5dois
x 3 000
= 4500
metros.
João
corre
dois
desses
trechos,de
Maria
corre
três.
x3
000
= 4500
metros.
Outra
solução:
aévelocidade
Maria
é 3/2
= 1,5
a de João, já 1800
que ele corre 1200 metros
2400
Outra solução:1,5
a velocidade
de Maria
3/2 = 1,5 vezes
a de
João,
já vezes
que ele
QUESTÃO 10 no mesmo tempo que ela corre 1800 metros. Logo, enquanto este corre 30001200
metros, ela corre
corre 1200 metros no mesmo tempo que ela corre 1800 metros. Logo, enquanto
ALTERNATIVA B x 3 000 = 4500 metros.
este corre 3000 metros,1,5
ela corre 1,5 x 3 000 = 4500 metros.
1200
1800
QUESTÃO 10
Para facilitar a notação, vamos escrever (R) para
QUESTÃO
10
ALTERNATIVA
B
representar
a área da região
R. Vamos nomear as quatro regiões
QUESTÃO
10
ALTERNATIVA
B
amarelas pelas
letras
Q, R e S,aconforme
figura ao (R) para
ParaP, facilitar
notação,indicado
vamosnaescrever
ALTERNATIVA
B QUESTÃO
10
lado.
Para
facilitar
a
notação,
vamos
escrever
(R) para
representar
a área daBregião R. Vamos nomear as quatro
regiões
ALTERNATIVA
Para facilitar arepresentar
notação,
vamos
escrever
(R)
para
representar
a
área
da
R. Vamos
a pelas
área da
região
R. R
Vamos
nomear as
quatroregião
regiões
amarelas
letras
P, Q,
e S, conforme
indicado
na
figura
ao
Observemos
que
(P)
=
(Q).
De
fato,
as
duas
regiões
são
nomear as quatro
regiões
amarelas
pelas
letras
P,
Q,
R
e
S,
conforme
indicado
na figura
amarelas
Q, R e S,
figura ao(R)
Para P,facilitar
a conforme
notação, indicado
vamos na
escrever
para
lado. pelas letras
as mesmas medidas de base e altura. Temos: (Q)
ao lado. triângulos
lado.com representar
a área da região R. Vamos nomear as quatro regiões
= (1/2) x 4 = 2, Observemos
pois Q é a que
metade
um paralelogramo
formado
por quatro triângulos
(P)
=de(Q).
fato,
as duas
regiões
são
letras
P, regiões
Q,
R e De
S,
conforme
indicado
na mesmas
figura
ao
Observemos que (P) =amarelas
(Q). De pelas
fato, as
duas
são
triângulos
com
as
menores. triângulos
Observemos
que
(P) = medidas
(Q). De fato,
as duas
regiões
são (Q)
com
as
mesmas
de
base
e
altura.
Temos:
lado.
medidas de base e altura. Temos: (Q) = (1/2) x 4 = 2, pois Q é a metade de um paralelogramo
triângulos
de basede
e altura.
Temos: (Q) formado por quatro triângulos
= (1/2)com
x 4as=mesmas
2, pois medidas
Q é a metade
um paralelogramo
formado por quatro
triângulos
menores.
Por
outro
lado,
a
região
R
é
a
parte
central
de
um
= (1/2)
x 4 = 2,Observemos
pois Q é aque
metade
formado
por quatro triângulos
(P) = de
(Q).um
De paralelogramo
fato, as duas regiões
são
menores.
hexágono
formado
6 triângulos
menores,
obtida formado
tomandopor 6 triângulos
Por outro
lado,menores.
a região
R épor
a parte
de
um
hexágono
triângulos
com central
as mesmas
medidas
de base e altura.
Temos: (Q)
sempre
metadePor
de outro
cada lado,
um desses
triângulos,
conforme
menores,
obtida atomando
sempre
um
a de
região
é desses
a parte
central
de um
= (1/2)
x 4 a=metade
2, pois
Q cada
é a Rmetade
de triângulos,
um
paralelogramo
formado por quatro triângulos
indicado
na
figura
ao
lado.
Logo,
(R)
=
6
x
(1/2)
=
3.
Por
outro
lado,
a
região
R
é
a
parte
central
de
um
formado
por
6
triângulos
menores,
obtida
tomando
conforme indicadohexágono
na figura
ao
lado.
Logo,
(R)
=
6
x
(1/2)
=
3.
menores.
hexágono
formado
por de
6 triângulos
obtida tomando
sempre
a metade
cada
um menores,
dessesa triângulos,
conforme
Finalmente, obtemos
que
(S)
= 7. De
fato,
decompondo
região S em
4
Finalmente,
obtemos
que
(S)um
= 7.desses
De fato,triângulos,
decompondo
a região
S em 4
sempre
a
metade
de
cada
conforme
Por
outro
lado,
a
região
R
é
a
parte
central
de um
indicado
na
figura
ao
lado.
Logo,
(R)
=
6
x
(1/2)
=
3.
regiões, regiões,
temos um
triângulo
menor
no centro
de Sde
e três
triângulos
iguais em
um
triângulo
menor
no
centro
S
e
três
triângulos
iguais
em
seu
indicado hexágono
na figura aoformado
lado. Logo,
= 6 x (1/2)menores,
= 3.
por (R)
6 triângulos
obtida tomando
seu entorno,
como
indicado
na
figura
ao
lado.
O
triângulo
central
tem
área
entorno, como indicado
na figura
ao lado.
O triângulo
central
tem área 1a eregião
os S em 4
Finalmente,
obtemos
que (S)
7. De fato,
decompondo
sempre
a metade
de cada
um= desses
triângulos,
conforme
1 e os outros
têm
área
2,
pois
são
a
metade
de
um
paralelogramo
formado
por
4
triângulos
outrostrês
três,
têm
área
2,
pois
são
a
metade
de
um
paralelogramo
formado
por
4
Finalmente,
obtemos
que
(S)
=
7.
De
fato,
decompondo
a
região
S
em
regiões,
um triângulo
menor
centro
e três
em4 seu
indicado
na figura ao
lado.no
Logo,
(R) =de
6 xS(1/2)
= 3.triângulos iguais
triângulos
menores.
Assim,
(S)
=
1
+
3
x
2
=
7.
menores.
Assim,
(S)
=
1
+
3
x
2
=
7.
regiões,
um como
triângulo
menornanofigura
centro
S eO três
triângulos
em seu
entorno,
indicado
ao de
lado.
triângulo
centraliguais
tem área
1 e os
entorno,
como
indicado
na
figura
ao
lado.
O
triângulo
central
tem
área
1
e
os
Finalmente,
obtemos
que
(S)
=
7.
De
fato,
decompondo
a
região
outros
três,
têm
área
2,
pois
são
a
metade
de
um
paralelogramo
formado
porS4em 4
Consequentemente, a área total destacada em amarelo é igual a
Consequentemente,
a área
total
destacada
emum
amarelo
é igual aformado
2 x (Q) +por
(R)4 + (S) =
outros
três,
têm
área
2,
pois
são
a
metade
de
paralelogramo
menor
triângulos
= 1 +no3 xcentro
2 = 7. de S e três triângulos iguais em seu
2 x (Q) + (R) + (S) =
(2 xregiões,
2) + menores.
3 +um
7 = triângulo
14.Assim, (S)
(2 x 2)triângulos
+ 3 + 7 = 14.
menores.
Assim,
(S) = 1na
+ 3figura
x 2 = ao
7. lado. O triângulo central tem área 1 e os
entorno,
como
indicado
Consequentemente,
áreasão
total
é igual formado
a 2 x (Q)por
+ (R)
outros
três, têm área 2, apois
a destacada
metade de em
um amarelo
paralelogramo
4 + (S) =
QUESTÃO
QUESTÃO
11 (211x Consequentemente,
aAssim,
área total
destacada
em
amarelo é igual a 2 x (Q) + (R) + (S) =
2)
+
3
+
7
=
14.
triângulos
menores.
(S)
=
1
+
3
x
2
=
7.
ALTERNATIVA E
(2Depois
x 2)
+ 79 =pulos
14. Luciana retornará à posição marcada com o número 1, conforme
ALTERNATIVA
E + 3de
QUESTÃO 11
Consequentemente,
a área total destacada em amarelo é igual a 2 x (Q) + (R) + (S) =
indicado
na
sequência
seguinte:
Depois de
9 pulos,
Luciana
retornará
à posição marcada com o número 1, conforme indicado na sequência seguinte:
ALTERNATIVA
E
QUESTÃO
11
(2 x 2) + 3 + 7 = 14.
ALTERNATIVA
E de 9 pulos Luciana retornará à posição marcada com o número 1, conforme
Depois
Depois
de
911
pulos seguinte:
Luciana retornará à posição marcada com o. número 1, conforme
indicado
na sequência
QUESTÃO
indicado ALTERNATIVA
na sequência seguinte:
E
Como 999
= 111
que
deLuciana
999
pulos
Luciana
estará
na
posição
marcada
com1,oconforme
número 1;
Depois
dedepois
9 pulos
retornará
à posição
marcada
com
o número
Como
999 x= 9,
111concluímos
x 9, concluímos
que
depois
de 999
pulos
Luciana
estará
na
posição
marcada
.
consequentemente,
depois
de
pular
1000
vezes,
ela
estará
na
posição
seguinte,
a
qual
está
marcada
com
o
número
5.
indicado
na
sequência
seguinte:
com o número 1; consequentemente, depois de pular 1000 vezes ela estará na. posição
marcada com
o número
5. x 9, concluímos que depois de 999 pulos Luciana estará na posição marcada
Como
999 = 111
Como
999o =número
111 x 9,1;concluímos
que depoisdepois
de 999 de
pulos
Luciana
com
consequentemente,
pular
1000 estará
vezesna
elaposição
estarámarcada
.na posição
QUESTÃO 12
commarcada
o número
1;o consequentemente,
depois de pular 1000 vezes ela estará na posição
com
número
5.
ALTERNATIVA E
marcadaComo
com o número
5. x 9, concluímos que depois de 999 pulos Luciana estará na posição marcada
111
Seja α uma 999
letra=qualquer
de A até Z. O número de códigos do tipo AAα é 26.
QUESTÃO
12
com o número 1; consequentemente, depois de pular 1000 vezes ela estará na posição
O número
de
códigos
do
tipo
Aαα
ALTERNATIVA
E o númeroé5.26 x 26 = 676 e o número de códigos do tipo ααα
QUESTÃO
12
marcada
com
Eα uma
é 26 xALTERNATIVA
26 x 26 =Seja
17576.
Se oletra
último
livro codificado
na Oordem
AAA,
qualquer
de A até Z.
número
de AAB,...,
códigos ABA,...
do tipo éAAα é 26.
1 5 9 4 8 3 7 2 6 1
1 5 9 4 8 3 7 2 6 1
1 5 9 4 8 3 7 2 6 1
1 5 9 4 8 3 7 2 6 1
Seja
uma
letradepois
qualquer
de
Aéaté
O =número
códigos
tipo Bαα,
AAα
26.ααα
DAB, então
ele
foiαregistrado
deAαα
codificados
todos
livros
dos
códigos
Aαα,
QUESTÃO
12
O número
de
códigos
do tipo
26 xZ.26
676
e ode
número
dedocódigos
do étipo
EDAA.
número
códigos
do
tipoSe
Aαα
ésua
26 xordem
26 =codificado
676
e o número
de códigos
ααα é
Cαα eOmais
o ALTERNATIVA
livro
código
Logo,
numérica
é do
676tipo
+ ABA,...
é 26
x de
26de
x 26
= 17576.
o último
livro
na classificação
ordem
AAA, AAB,...,
Seja
α
uma
letra
qualquer
de
A
até
Z.
O
número
de
códigos
do
tipo
AAα
é
26
x
26
x
26
=
17576.
Se
o
último
livro
codificado
na
ordem
AAA,
AAB,...,
ABA,...
é é 26.
676 + 676 + 2 = 2030.
Solução da prova da 1ª Fase
OBMEP 2016 – Nível 2
5
QUESTÃO 12
ALTERNATIVA E
Seja α, β e γ letras quaisquer de A até Z. O número de códigos do tipo AAα é 26. O número de códigos do tipo Aαβ é 26
x 26 = 676 e o número de códigos do tipo αβγ é 26 x 26 x 26 = 17576. Se o último livro codificado na ordem AAA, AAB,...,
ABA,... é DAB, então ele foi registrado depois de codificados todos livros dos códigos Aαβ, Bαβ, Cαβ e mais o livro de
Solução mais detalhada: O livro recebeu o código DAB depois de todos os demais
código DAA. Logo, sua ordem numérica na classificação é 676 + 676 + 676 + 2 = 2030.
livros, que receberam os códigos que:
Solução mais detalhada:
O livro
o código
i) iniciam com
a recebeu
letra A, a
saber: DAB depois de todos os demais livros, que receberam os códigos que:
i) iniciam com a letra A,
a saber:
AAA,
AAB, até AAZ, num total de 26 livros;
ABA,
livros;
AAA, AAB, até
AAZ,ABB,
num até
totalABZ,
de 2626
livros;
ABA, ABB, até...ABZ, 26 livros;
AZA, AZB,...,AZZ, 26 livros.
Até este ponto foram codificados 26 x 26 = 676 livros.
AZA, AZB,...,AZZ, 26 livros.
ii) iniciam com a letra B, isto é, BAA, BAB,..., BAZ, BBA,..., BBZ,..,BZA, BZB,... BZZ,
Até este
ponto
codificados
26livros.
x 26 = 676 livros.
num
totalforam
de 26
x 26 = 676
ii) iniciam comiii)
a letra
B, isto
é, BAA,
BBZ,..,BZA,
BZZ,
num total de 26 x 26 = 676 livros.
iniciam
com
a letraBAB,...,
C, de BAZ,
formaBBA,...,
análoga,
num totalBZB,...
de 676
livros
iii) iniciam come,afinalmente,
letra C, de forma análoga, num total de 676 livros.
iv) iniciam
a letra
D, totalizando
somente
doisDAA
livros:
DAA
DAB (o último).
iv) iniciam finalmente
comcom
a letra
D, totalizando
somente
dois livros:
e DAB
(o eúltimo).
Portanto,
o
número
de
livros
da
biblioteca
é
3
x
676
+
2
=
2030.
Portanto, o número de livros da biblioteca é 3 x 676 + 2 = 2030.
...
QUESTÃO 13
ALTERNATIVA A
QUESTÃO 13
Sejam M e N os dois números, sendo M o número que ao se retirar o último algarismo
ALTERNATIVA
A indicaremos por b) resulta no número N. Do enunciado podemos concluir que
(o qual
M+
N =números,
1357 e M
= 10N
b. Portanto,
Sejam M e N os
dois
sendo
M o+número
que ao se retirar o último algarismo (o qual indicaremos por b) resulta
no número N. Do enunciado, podemos concluir que M + N = 1357 e M = 10N + b. Portanto,
10N + b + N = 1357 => 11N + b = 1357
10N + b + N = 1357, ou seja, 11N + b = 1357
Como
1357
resto
4 na
divisão
que
11N
+ bb=– 1353
4
Como 1357 deixa
resto
4 nadeixa
divisão
por 11,
temos
que por
11N 11,
+ b =temos
11 x 123
+ 4.
Logo,
4 = 11+x 4.
123Logo
– 11Nb.–Portanto,
b–4
é múltiplo de 11.
Como
b é–um
algarismo,
b sóbpode
igual a de
4. 11. Como b é um algarismo, b só pode
= 11
x 123
11N
. Portanto,
– 4 éser
múltiplo
ser igual a 4.
QUESTÃO 14
QUESTÃO 14
ALTERNATIVA
C
ALTERNATIVA
C
A área do quadrilátero ACDF é a soma das áreas dos triângulos ACD e
A área do quadrilátero ACDF é a soma das áreas dos triângulos ACD e ADF. O triângulo ACD
ADF. O triângulo ACD tem base CD = 2 e altura AB = 10 relativa à base
tem base CD = 2 e altura AB = 10 relativa à base CD, enquanto o triângulo ADF tem base FA =
CD, enquanto que o triângulo ADF tem base FA = 6 e altura DE = 7
6 e altura DE =
7 relativa
à baseFA.
FA.Logo
Logo,aa área
área do
é (2é x(210)
2 =÷102 e=a10
área
relativa
à base
dotriângulo
triânguloACD
ACD
x ÷10)
ea
do triângulo ADF
é
(6
x
7)
÷
2
=
21.
Somando
essas
áreas,
obtemos
que
o
quadrilátero
ACDF
área do triângulo ADF é (6 x 7) ÷ 2 = 21. Somando essas áreas, obtemos
tem área 31. que o quadrilátero ACDF tem área 31.
QUESTÃO 15
ALTERNATIVA D
N1Q18
QUESTÃO 16
ALTERNATIVA B
Consideremos n um número inteiro positivo e,
seguindo o padrão indicado pelas flechas, vamos
acompanhar o preenchimento das n primeiras casas da
tabela. Observemos que n será um quadrado perfeito
somente no caso em que a tabela formada pelas casas
preenchidas for quadrada. Isso ocorre apenas quando a
Solução mais detalhada: O livro recebeu o código DAB depois de todos os demais
livros, que receberam os códigos que:
i) iniciam com a letra A, a saber:
AAA, AAB, até AAZ, num total de 26 livros;
Solução da prova da 1ª Fase
6
ABA, ABB, até ABZ, 26 livros;
OBMEP 2016 – Nível 2
...
AZA, AZB,...,AZZ, 26 livros.
Até este ponto foram codificados 26 x 26 = 676 livros.
QUESTÃO 15
ALTERNATIVAii)Diniciam com a letra B, isto é, BAA, BAB,..., BAZ, BBA,..., BBZ,..,BZA, BZB,... BZZ,
num total de 26 x 26 = 676 livros.
Como o número total de bolas em cinco caixas consecutivas é sempre o mesmo, a quantidade de bolas da primeira até a
iii) iniciam com a letra C, de forma análoga, num total de 676 livros
quinta caixa deve ser igual à quantidade de bolas da segunda até a sexta caixa:
e, finalmente,
(no de bolas na Caixa
1) + 5 +com
9 + 1a+letra
( no de
na Caixa
5) =
iv) iniciam
D, bolas
totalizando
somente
dois livros: DAA e DAB (o último).
o
o
5
+
9
+
1
+
(n
de
bolas
na
Caixa
5)
+
(n
na+Caixa
6)
Portanto, o número de livros da bibliotecade
é 3bolas
x 676
2 = 2030.
Logo, (no de bolas na Caixa 1) = (no de bolas na Caixa 6).
Pelo mesmo motivo, começando da segunda caixa e depois na terceira caixa,
QUESTÃO 13
5 + 9 + 1 + (no deALTERNATIVA
A + (no de bolas na Caixa 6) =
bolas na Caixa 5)
Sejam
M e 5)
N +os(ndois
números,
sendo
o
o número que ao se retirar o último algarismo
9 + 1 + (no de bolas
na Caixa
de bolas
na Caixa
6) +M
(no
de bolas na Caixa 7).
(o qual indicaremos por b) resulta no número N. Do enunciado podemos concluir que
Logo, o número de
Caixa
7 é=5.10N + b. Portanto,
M bolas
+ N =na
1357
eM
De modo análogo, vemos que o número de bolas da Caixa 8 é 9, o número de bolas na Caixa 9 é 1, que a Caixa 10 possui
b+N
=>número
11N + bde=bolas
1357que o da Caixa 6, o qual é igual ao
o mesmo número de bolas que o da Caixa 510N
e a+
Caixa
11,=o1357
mesmo
número de bolas na Caixa 1, como vimos acima. As quantidades de bolas repetem-se a cada cinco caixas.
Como 1357 deixa resto 4 na divisão por 11, temos que 11N + b = 1353 + 4. Logo b – 4
Na ilustração há a informação de que as caixas contendo 3 e 7 bolas são vizinhas; para que isto ocorra, a Caixa 1 deve
= 11 x 123 – 11N . Portanto, b – 4 é múltiplo de 11. Como b é um algarismo, b só pode
conter 7 bolas e as caixas 5 e 6 devem conter, respectivamente, 3 e 7 bolas. Assim, os conteúdos das caixas formam a
ser igual a 4.
sequência 7, 5, 9, 1, 3, 7, 5, 9, 1, 3 ....
De fato, não podeQUESTÃO
ocorrer que
14a primeira caixa contenha 3 bolas, pois isto geraria a sequência 3, 5, 9, 1, 7, 3, 5, 9, 1, 7, ...
ALTERNATIVA
C
e a ordem entre 3 e 7 seria incompatível
com o que aparece na ilustração no enunciado.
A área do quadrilátero ACDF é a soma das áreas dos triângulos ACD e
Para descobrir o conteúdo da Caixa 2016, fazemos a divisão de 2016 por 5; o resto é 1 e isto nos diz que o conteúdo da
ADF. O triângulo ACD tem base CD = 2 e altura AB = 10 relativa à base
Caixa 2016 é o mesmo que o da Caixa 1, ou seja, que a Caixa 2016 contém 7 bolas.
CD, enquanto que o triângulo ADF tem base FA = 6 e altura DE = 7
Solução 2: (utilizando
Álgebra)
relativa
à base FA. Logo a área do triângulo ACD é (2 x 10) ÷ 2 = 10 e a
ADFde
é (6
x 7)distribuídas
÷ 2 = 21. em
Somando
essas
áreas, obtemos
Sejam x1, x2, x3, área
x4, x5 do
e xtriângulo
os números
bolas
seis caixas
consecutivas,
respectivamente. Como o
6
que
o
quadrilátero
ACDF
tem
área
31.
número total de bolas em cincos caixas consecutivas é sempre o mesmo, segue que x1 + x2 + x3 + x4 + x5 = x2 + x3 + x4 +
x5 + x6 e, consequentemente, x1 = x6. Assim, caixas cujos números diferem por cinco unidades contêm o mesmo número
de bolas. Como em
duas caixas
QUESTÃO
15 consecutivas aparecem 3 e 7 bolas, concluímos que os conteúdos das caixas formam a
sequência 7, 5, 9,ALTERNATIVA
1, 3, 7, 5, 9, 1, 3 ...,
D pois a outra possibilidade, 3, 5, 9, 1, 7, 3, 5, 9, 1, 7 ..., é incompatível com a informação
da ilustração. Assim,
a
caixa
de
número
2016 contém a mesma quantidade de bolas que a Caixa 1, a saber, 7 bolas.
N1Q18
QUESTÃO 16 QUESTÃO 16
ALTERNATIVA B
ALTERNATIVA B
Consideremos
número
inteiro
positivo
Consideremos n um número
inteiro positivone, um
seguindo
o padrão
indicado
pelase,
seguindo oo preenchimento
padrão indicado
pelas casas
flechas,
vamos
flechas, vamos acompanhar
das n primeiras
da tabela.
o preenchimento
dasnoncaso
primeiras
Observemos queacompanhar
n será um quadrado
perfeito somente
em que casas
a tabelada
tabela.
Observemos
que
n
será
um
quadrado
perfeito
formada pelas casas preenchidas for quadrada. Isso ocorre apenas quando
somente estiver
no caso
em que coluna
a tabela
formada
a última casa preenchida
na primeira
(quando
n for pelas
par) oucasas
na
2
preenchidas
for Como
quadrada.
quando a
primeira linha (quando
n for ímpar).
2016 =Isso
2025ocorre
– 9 = 45apenas
– 9, observamos
que 2016 aparecerá
na 45ª
coluna
e 10ª linha,
uma vez
2025 coluna
= 452 estará
na
última
casa
preenchida
estiver
na que
primeira
(quando
1ª linha e 2016 estará nove linhas abaixo.
respectivamente. Como o número total de bolas em cincos caixas consecutivas é sempre o
mesmo, segue que x1 + x2 + x3 + x4 + x5 = x2 + x3 + x4 + x5 + x6 e, consequentemente, x1 = x6.
Assim, caixas cujos números diferem por cinco unidades contêm o mesmo número de bolas.
Como em duas caixas consecutivas aparecem 3 e 7 bolas, concluímos
queda
osprova
conteúdos
Solução
da 1ª das
Fase
caixas formam a sequência 7, 5, 9, 1, 3, 7, 5, 9, 1, 3 ..., pois a outra possibilidade,
3,
5,
9, 2
OBMEP 2016 – Nível
1, 7, 3, 5, 9, 1, 7 ..., é incompatível com a informação da ilustração. Assim, a caixa de
número 2016 contém a mesma quantidade de bolas que a Caixa 1, a saber, 7 bolas.
QUESTÃO 17
QUESTÃO 19
ALTERNATIVA
C
ALTERNATIVA
C
O retângulo
perímetromaior
do ABCD
retângulo
maior
ABCD da
é igual
ao
1ª solução:1ªO solução:
perímetro do
é igual
ao perímetro
figura em
perímetro
figura
emretângulos
forma de(os
cruz
formada
cinco
retângulos
forma de cruz
formadada
pelos
cinco
que
possuempelos
números
marcados
em
vermelho,
ilustração
ao lado).
O perímetro
dessa
seu interior(destacados
e o retângulo em
cinza),
como nana
ilustração
ao lado.
O perímetro
dessa figura
é
igual à soma
das medidas
todos os
lados
dos quatro
menos
as
figura
é igual de
à soma
das
medidas
de retângulos
todos os externos,
lados dos
quatro
de cada umretângulos
de seus lados
que coincidem
lados
do retângulo
somaque
das
externos,
menoscom
asosde
cada
um de cinza.
seus Alados
medidas decoincidem
todos os lados
desses
quatro
retângulos
externos
é
16
+
18
+
26
+
14
=
74
e
com os lados do retângulo cinza. A soma das medidas de
o perímetrotodos
da figura
em forma
de cruz
é 54,retângulos
pois ele é igual
ao perímetro
os lados
desses
quatro
externos
é 16 +do18retângulo
+ 26 +
ABCD. Logo,
o
perímetro
do
retângulo
cinza
é
74
–
54
=
20
cm.
14 = 74 e o perímetro da figura em forma de cruz é 54, pois ele é
A
7
B
C
igual ao perímetro do retângulo ABCD. Logo, o perímetro do D
2ª solução (exige alguns
conhecimentos
de
Álgebra):
2ª solução
alguns
conhecimentos
deconhecimentos
Álgebra):
retângulo cinza
é 74 – (exige
54 = 20
cm.
2ª
solução
(exige alguns
de Álgebra):
2ª solução (exige alguns conhecimentos de Álgebra):
Assolução
letras de
a até
f naAsfigura
medidas
dos lados
2ª
(exige
alguns
conhecimentos
def Álgebra):
letrassão
de as
a até
naletras
figura
são
as fmedidas
As
dede
a cada
até
na figurados
sãolados
as medidas dos lados
dosletras
retângulos
menores.
Calculando
o
perímetro
As
de As
a até
f
na
figura
são
as
medidas
dos
lados
dos
retângulos
menores.
dos
retângulos
menores.
Calculando
o
perímetro
de
cada
letras de a até f na figura
são
as
medidas
dos
lados
dos
retângulos
menores. Calculando
o perímetro de cada
b
d
2
2
16
Calculando odos
perímetro
de cada
um dos retângulos
menores,
temos:
2b de
2dcada
16
retângulos
menores.
Calculando
o perímetro
2b 2d
16
2a 2e
182b 2d
a 2e
216
18
2a 2e
18
2e
14 2temos:
um dos retângulos menores,
temos: 2c menores,
a 2e
18
c
e
2
2
14
um dos retângulos
14
um dos retângulos menores, temos: 2c 2e
2b temos:
2f
26 2c 2e
um dos retângulos menores,
b 2f
214
26
2b 2f
26
2b 2e
? 2b 2f
b 2e
226
?
2b 2e
?
2b 2e
?
O perímetro do retângulo
maior ABCD
é
O perímetro
do retângulo
maior
é maior ABCD é
O perímetro
doABCD
retângulo
2 a b c O
2perímetro
b2
a
2
b
2
c
2
d
2
e
2
f
54.
d e2fado
retângulo
c 2 dmaior
e ABCD
f 2aé 2b 2c 2d 2e 2f 54.
O perímetro do retângulo maior ABCD é 2 a b c 2 d e f 2a 2b 2c 2d 2e 2f 54.
Somando os2perímetros
redor
central
c dos
2 dquatro
os
e perímetros
fretângulos
b ao
2quatro
c 2ddo
2retângulo
e 2f 54.
a b Somando
2a 2dos
retângulos
ao
redor cujas
do retângulo
central
Somando
osdo
perímetros
dos quatro
aodadas,
redor
do cujas
retângulo central c
Somando
os perímetros
dos quatro retângulos
ao redor
retângulo central
cujasretângulos
medidas são
temos:
medidas são
dadas,
temos:
são dadas,
temos:
Somandomedidas
os perímetros
dos
quatro
retângulos
ao
redor
do
retângulo
central
cujas
medidas são dadas, temos:
+e2ddadas,
2
b2+b22ef 2=c22
2fb2
2
2.f + 2b + 2e
2b 2medidas
d 2a2b2são
2+c22
ba2+d2
c
2+f22bd2+b22ce2+e2
ba2
+e2temos:
de2+b22ac2+f 22ee22+ab22c
+2e2
2e.2e 2f 2b 2
2d 2
2e
ca
2e 2maior
b 2f d 2a2e 2b2f22
cb2d
perímetro
do
retângulo
perímetro
doaretângulo
maior
perímetro do retângulo maior
2b 2d 2a 2e 2c 2e 2b 2f 2a 2b 2c 2d 2e 2f 2b perímetro
2e . do retângulo maior
Assim 16 18 14 26
.bPortanto,
o
perímetro
5416
2b18
2e14
226
b 254
e 74
54
20
perímetro
do
retângulo
maior
Assim,
Assim
.
Portanto,
o perímetro
2
b
2
e
2
2
e
74
54
20
Assim 16 18 14 26 54 2b 2e 2b 2e 74 54
20 . Portanto, o pe
do
retângulo
cinza
é
20
cm.
do
retângulo
cinza
é
20
cm.
Assim 16
.
Portanto,
o
perímetro
retângulo
18
14 cinza
26
é54
2
b
2
e
2
b
2
e
74
54
20
Portanto, o perímetro
do
20
cm.
do retângulo cinza é 20 cm.
do retângulo cinza é 20 cm.
QUESTÃO
QUESTÃO 2018
QUESTÃO 20
ALTERNATIVA E E ALTERNATIVA E QUESTÃO 20
ALTERNATIVA
QUESTÃO 20
ALTERNATIVA
E a aplicação de dois procedimentos
Solução 1: Uma sequência
com1:três
números
é obtida
Solução
sequência
com após
três números
é obtida após a aplicação de dois procedimentos
ALTERNATIVA
E Uma
Solução
1:
Umaapós
sequência
três
números
é obtida após
aplicação
de dois proc
Solução
Uma
sequência
com
três
números
é
obtida
a aaplicação
de
dois
a apartir
do primeiro
a partir do1:primeiro
número,
finalizando
no
terceiro
número
igual
1. com
Vamos
fazer
a procedimentos
contagem
a
partir
do
primeiro
número,
finalizando
no
terceiro
número
igual
adois
1. Vamos
fazer
a contagem
Solução
1:
Uma
sequência
com
três
números
é
obtida
após
a
aplicação
de
procedimentos
a
partir
do
primeiro
número,
finalizando
no
terceiro
número
igual
a
1.
Vamos
das sequências
a partir
da
quantidade
de
algarismos
do número
número,
finalizando
nodas
terceiro
número
ada1.quantidade
Vamos
fazer
a contagemdodas
sequências
a partir da quantidade defazer a
sequências
a igual
partir
de inicial.
algarismos
número
inicial.
a
partir
do
primeiro
número,
finalizando
no
terceiro
número
igual
a
1.
Vamos
fazer
a número
contagem
das
sequências
a
partir
da
quantidade
de
algarismos
inicial.
número
inicial
com 3 número
algarismos:
nesse
caso
o único procedimento
usado
foiprocedimento
o dedo
inicial
com
3 algarismos:
nesse caso
o único
usado foi o de
algarismos
dodas
número
inicial.
sequências
a partir da quantidade
denúmero
algarismos
do com
número
inicial.
inicial
3
algarismos:
nesse
caso
o
único
procedimento usad
apagar o algarismo dasapagar
unidades
(duas vezes,
consecutivamente).
Nesta
situação,
o algarismo
das unidades
(duas
vezes,
consecutivamente).
Nesta
situação,
número
com
3 algarismos:
caso
o
único
procedimento
usado
foi
o
de
• número inicial
com 3inicial
algarismos:
nesseapagar
caso
onesse
único
procedimento
usado
foi
o
de
apagar
o
algarismo
das Nesta
oalgarismo
algarismo das
das unidades),
unidades (duas
vezes, consecutivamente).
o número inicial é impar
(5
possibilidades
para
o
com
o
o
número
inicial
é
impar
(5
possibilidades
para
o
algarismo
das
unidades),
com
o
apagar
o
algarismo
das
unidades
(duas
vezes,
consecutivamente).
Nesta
situação,
unidades
vezes, consecutivamente).
número
inicial
é ímparpara
(5 possibilidades
paraunidade
o Nesta
número
inicial é oimpar
(5 possibilidades
o algarismo das
algarismos(duas
das dezenas
também ímpar
(também
5situação,
possibilidades
para
o5algarismo
algarismos
das dezenas
também
ímparo (também
possibilidades
para
ooalgarismo
o número
inicial
é impar
(5 possibilidades
para
algarismo
das
unidades),
com
algarismos
das
dezenas
também
ímpar
(também
5
possibilidades
o
algarismo
das
unidades),
com
o
algarismos
das
dezenas
também
ímpar
(também
5
possibilidades
para
opara o
das dezenas), e com das
o algarismo
das
centenas
igual a das
1 (acima
de 199,
não
dezenas),
e com
oímpar
algarismo
centenas
igual para
a 1 o(acima
de 199, não
algarismos
das
dezenas
também
(também
5
possibilidades
algarismo
dasdas
dezenas),
com ao 1algarismo
das
igual oa 11como
(acima de
algarismo
dezenas),
e com
o algarismo
centenas
(acima de
199,centenas
não obtemos
obtemos odas
1 como
terceiro
número
aplicando
apenas
2e igual
procedimentos).
Assim,
obtemos
o 1 ocomo
terceiro
número
aplicando
apenas
2 procedimentos).
das dezenas),
e com
algarismo
das
centenas
igual anúmero
1 (acima
de 199,apenas
não 2Assim,
obtemos
o
1
como
terceiro
aplicando
procedimento
terceiro
número
aplicando
apenas
2
procedimentos).
Assim,
existem
5
x
5
x
1
=
25
números
de
três
algarismos
existem 5 x 5 x 1 = 25
números
de
quedegeram
uma sequência
existem
5 xterceiro
5 xtrês
1 número
=algarismos
25 números
três algarismos
que geram Assim,
uma sequência
obtemos o
1 como
apenas
2 procedimentos).
existem
5aplicando
x 5 x 1 =
25 números
de três algarismos
que geram uma
que
geram
formada por três
números.
formada
poruma
trêssequência
números.
formada
por
três
números.
existem 5 x 5 x 1 = 25 números
depor
três
algarismos
que geram uma sequência
formada
três
números.
número inicial com
2número
algarismos:
necessariamente
usamos
dois procedimentos
procedimentos
•
algarismos:
usamos
dois
diferentes
para formá-la:
2por
inicialnecessariamente
com 2 algarismos:
necessariamente
usamos
dois procedimentos
formada
três números.
algarismos
número inicial
com 2 (se
algarismos:
necessariamente
usamos dois proc
diferentes para
formá-la:
apagamos
o
das
unidades
iniciar
por
um
apagamos
os
algarismos
das
unidades
(se
iniciar
por
um
ímpar)
ou
dividimos
por
2
(se
iniciar
porpor
umum
par),
diferentes
formá-la: apagamos
o algarismos
dasdois
unidades
(se iniciar
número inicial
compara
2 algarismos:
necessariamente
usamos
procedimentos
diferentes
para
formá-la:
apagamos
o
algarismos
das
unidades (se inici
ímpar)
ou
dividimos
por
2
(se
iniciar
por
um
par),
nessa
ordem
ou
vice
e
versa.
nessa ordem diferentes
ou vice-versa.
ímpar)
ou dividimos
por 2 (se
iniciar
por um
par),
nessa ordem
ou vice
eum
versa.
para formá-la:
apagamos
o dividimos
algarismos
das
unidades
(seum
iniciar
ímpar) ou
por
2 (pois
(se
iniciar
por
par),por
nessa
ordem ou vice e ve
Se o primeiro número
for
ímpar,
o
algarismo
das
dezenas
é
2
deve
ser
o
Se
primeiro
número
for
ímpar,
algarismo
das
2 (pois deve
serapós
o
ímpar)número
ou dividimos
por 2 o(se
iniciar
por
um
par),onúmero
nessa
oudezenas
vice
e versa.
• Se o primeiro
for oímpar,
algarismo
das
dezenas
é 2ordem
(pois
deve
ser
o éresultado
obtido
Se
o
primeiro
for
ímpar,
o
algarismo
das
dezenas
é 2 (pois d
resultado obtido após resultado
apagar o obtido
seu algarismo
das unidades).
Nesse das
caso,
após
apagar
o
seu
algarismo
unidades).
Nesse
caso,
Se
o
primeiro
número
for
ímpar,
o
algarismo
das
dezenas
é
2
(pois
deve
ser
o
apagar o seu algarismo das unidades). Nesse
caso, temos
5após
possibilidades.
resultado
obtido
apagar
o
seu
algarismo
das
unidades).
Ne
temos 5 possibilidades.temos 5 possibilidades.
resultado obtido após apagar
o
seu
algarismo
das
unidades).
Nesse
caso,
temosa 5sua
possibilidades.
Se o primeiro número
foro par,
o segundo
Nesse
o
Se
primeiro
númeroé for
par,metade.
o segundo
é acaso,
sua metade.
Nesse caso, o
temos5 possibilidades.
Se
o
primeiro
número for
par, o segundo
é a sua metade. Ness
segundo termo deve ser
ímpar
(para
usarmos
o
procedimento
de
apagar
o
segundo
termo
deve
ser
ímpar
(para
usarmos
o
procedimento
o
Se o primeiro número for par,
o segundo
édeve
a sua
metade.
Nesse
caso,deoo apagar
segundo
termo
ser
ímpar
(para
usarmos
procedimento de
algarismo das unidades).
Como, após
apagar asComo,
unidades,
devemos
obter
1, o
algarismo
das
unidades).
após
apagar
as
unidades,
devemos
obter
1,
o
segundo termo deve ser ímpar
(para das
usarmos
o procedimento
deapagar
apagar
algarismo
unidades).
Como,
após
as ounidades, devemos
número obtido é ímpar
entre
10
e
20.
Nesse
caso,
também
temos
5
número obtido é ímpar entre 10 e 20. Nesse caso, também temos 5
Solução da prova da 1ª Fase
OBMEP 2016 – Nível 2
•
8
Se o primeiro número for par, o segundo é a sua metade. Nesse caso, o segundo termo deve ser ímpar
(para usarmos, em continuação, o procedimento de apagar o algarismo das unidades). Como, após
apagar as unidades, devemos obter 1, o número obtido no estágio intermediário é ímpar entre 10 e 20.
Nesse caso, também temos 5 possibilidades.
Assim, existem 5 + 5 = 10 números de dois algarismos que geram uma sequência formada por três números.
• número inicial com 1 algarismo: temos duas sequências, uma com o número inicial igual a 4 e outra iniciando
por 3.
Logo, o número de sequências formadas por três números é 25 + 10 + 2 = 37.
A tabela abaixo mostra as possíveis sequências formadas por três números. Para isso, usamos as letras u e d,
para representar, respectivamente, o algarismo das unidades e das dezenas do número inicial.
Número
inicial
Observação
1º procedimento
Número intermediário
2º procedimento
Quantidade de
sequências
1du
d e u ímpares
apaga unidade
1d
apaga unidade
5 x 5 = 25
2u
u ímpar
apaga unidade
2
divide por 2
5
du
u par
divide por 2
ímpar entre 10 e 20
apaga unidade
5
u=4
divide por 2
2
divide por 2
1
u=3
soma 1 e divide por 2
2
divide por 2
1
total de sequências
37
Solução 2: As sequências descritas no enunciado que começam com números de apenas um algarismo são:
2→1, 3→2→1, 4→2→1, 5→3→2→1, 6→3→2→1, 7→4→2→1 e 8→4→2→1 e 9→5→3→2→1.
Destas, somente duas têm três termos: a que começa com 3 e a que começa com 4.
Há apenas as seguintes sequências com dois termos: 2→1, 11→1, 13→1, 15→1, 17→1 e 19→1. Utilizando-as, há
dois procedimentos para se obter sequências com três termos:
1) Colocando-se como primeiro termo da sequência o dobro dos números iniciais das sequências com dois termos
exibidas acima:
4→2→1, 22→11→1, 26→13→1, 30→15→1, 34→17→1 e 38→19→1.
Observe que 4→2→1 já havia sido contada antes e, portanto, no total, até agora, temos sete sequências de três
termos.
2) Colocando-se como primeiro termo da sequência números iniciados com 2 (ou seja, com 2 na casa das dezenas)
ou 11, 13, 15, 17 ou 19 (ou seja, com 1 na casa das centenas e um algarismo ímpar na casa das dezenas) e terminados
com um número ímpar na casa das unidades:
21→2→1, 23→2→1, 25→2→1, 27→2→1, 29→2→1
111→11→1, 113→11→1, 115→11→1, 117→11→1, 119→11→1
131→13→1, 133→13→1, 135→13→1, 137→13→1, 139→13→1
151→15→1, 153→15→1, 155→15→1, 157→15→1, 159→15→1
171→17→1, 173→17→1, 175→17→1, 177→17→1, 179→17→1
191→19→1, 193→19→1, 195→19→1, 197→19→1, 199→19→1
Assim, ao todo temos 7 + 30 = 37 sequências de três termos.
Solução da prova da 1ª Fase
OBMEP 2016 – Nível 2
9
QUESTÃO 19
ALTERNATIVA D
O problema pede que encontremos dois números consecutivos cujas somas de seus algarismos seja um múltiplo de 5.
Isto implica que a diferença entre as somas dos algarismos dos números consecutivos deve ser um múltiplo de 5.
Se a unidade de um número for diferente de 9, temos que a diferença entre as somas de seus algarismos com a soma
dos algarismos de seu sucessor é sempre 1; por exemplo, somando os algarismos de 24 obtemos 2 + 4 = 6 e, somando
os algarismos de 25, obtemos 2 + 5 = 7. Isto ocorre, pois a unidade é acrescida de 1 quando tomamos o sucessor e
os outros algarismos não se alteram. Isto restringe nosso trabalho em encontrar números consecutivos que terminem,
respectivamente, em 9 e 0 e atendam as exigências do enunciado.
Se a unidade de um número for 9, mas sua dezena for diferente de 9, a diferença entre as somas dos algarismos dos
números consecutivos será 8, pois, ao considerarmos a alteração que ocorre quando passamos de um número terminado
em 9 para o seu consecutivo, vemos que a unidade 9 se transforma em 0 e ocorre o aumento de 1 na dezena; por exemplo,
29 tem 11 como soma de seus algarismos e seu sucessor, 30, tem 3 como soma de seus algarismos. Neste caso, a
diferença entre as somas dos algarismos dos números consecutivos é igual a 8 e, portanto, esses números não atendem
o enunciado.
Se a unidade e a dezena de um número forem iguais a 9, mas a centena for diferente de 9, com o mesmo raciocínio, a
diferença entre as somas dos algarismos dos consecutivos será de 17, pois, ao considerarmos a alteração que ocorre,
passamos de um número deste tipo, terminado em 99 com centena diferente de 9, para o seu consecutivo, vemos que
os dois algarismos 9 finais viram 0 e que a centena é acrescida de 1; por exemplo, 399 tem soma de seus dígitos igual
a 21 e 400 tem soma de seus algarismos igual a 4. Neste caso, também, a diferença entre as somas dos algarismos dos
números consecutivos não é múltiplo de 5 e esses números não servem.
Do mesmo modo, para um número com três noves no final, mas com algarismo da casa de milhar diferente de 9, teremos
uma diferença entre as somas dos algarismos dos números consecutivos igual a 3 x 9 - 1 = 26 (também não servem),
mas, com quatro noves no final e dezena de milhar diferente de 9, essa diferença é 4 x 9 - 1 = 35 , a qual, felizmente, é
múltiplo de 5.
Só nos resta encontrar o menor número desse tipo que atenda as exigências do enunciado. Este número deve terminar com
9999 e a soma de seus dígitos deve ser múltiplo de 5. Como 4 x 9 = 36, devemos procurar o menor número que, somado
a 36, resulte em um múltiplo de 5. Este número é 4 e, portanto, o menor número com as propriedades especificadas no
enunciado é 49999. Assim, 49999 e 50000 são o penúltimo e o último números da lista de Juliana.
Portanto, a soma dos algarismos do penúltimo número da lista de Juliana é 4 x 9 + 4 = 40.
Solução da prova da 1ª Fase
OBMEP 2016 – Nível 2
10
QUESTÃO 20
ALTERNATIVA C
Vamos primeiro contar quantos pacotes distintos é possível fazer com qualquer número de figurinhas, incluindo o pacote
sem nenhuma figurinha. Para fazer um pacote, Bruno pode, por exemplo, escolher primeiramente quantas figurinhas
da Alemanha, depois quantas do Brasil e finalmente quantas da Colômbia ele deseja colocar no pacote. Pelo princípio
multiplicativo, isso pode ser feito de 6 x 7 x 5 = 210 maneiras diferentes; observemos que o fator 6 nessa expressão
corresponde ao fato de que Bruno tem 6 escolhas (a saber, 0, 1, 2, 3, 4, 5) para o número de figurinhas da Alemanha; já
o fator 7 é o número de escolhas para o número que figurinhas do Brasil e 5 é o número de escolhas para o número de
figurinhas da Colômbia que ele pode colocar no pacote.
Por outro lado, o número de pacotes com menos que três figurinhas é 10, como vemos na tabela abaixo (na segunda
coluna, usamos letras A, B e C para denotar Alemanha, Brasil e Colômbia, respectivamente):
Quantidade de
figurinhas escolhidas
para colocar no
pacote
0 figurinha
1 figurinha
2 figurinhas
O que fica dentro do pacote
Quantidade de
pacotes
nada
A ou B ou C
AA ou BB ou CC ou AB ou AC ou BC
Total
1
3
6
1 + 3 + 6 = 10
Segue, então, que o número de pacotes distintos com pelo menos três figurinhas é 210 – 10 = 200.
Outra solução: Um pacote com pelo menos três figurinhas poderá conter figurinhas com as três bandeiras diferentes, ou
figurinhas com somente duas das bandeiras ou ainda figurinhas com apenas uma das bandeiras. Vamos fazer a contagem
do número de pacotes distintos que podem ser feitos em cada um desses casos, com atenção para que sempre os
pacotes contenham, no mínimo, três figurinhas.
1. Pacotes de figurinhas com as três bandeiras diferentes
Bruno tem 5 possibilidades para o número de figurinhas com a bandeira da Alemanha que poderá colocar em um pacote:
A, AA, AAA, AAAA, AAAAA. Da mesma forma, terá 6 possibilidades para o número de figurinhas com a bandeira do
Brasil e 4 para figurinhas com a bandeira da Colômbia.
O número de pacotes distintos que Bruno poderá formar com pelo menos três figurinhas com as três bandeiras diferentes
será 5 x 6 x 4 = 120.
2. Pacotes de figurinhas com todas as figurinhas com a mesma bandeira
O número de pacotes distintos que Bruno poderá formar com pelo menos três figurinhas e todas as figurinhas no pacote
com a mesma bandeira é 3 + 4 + 2 = 9 (AAA, AAAA, AAAAA, BBB, BBBB, BBBBB, BBBBBB, CCC e CCCC).
3. Pacotes de figurinhas com bandeiras de exatamente dois países
Se os países forem, por exemplo, Alemanha e Brasil, teremos 5 x 6 – 1 possibilidades, já que os pacotes devem conter
pelo menos três figurinhas, e precisamos desconsiderar o pacote que tem apenas uma figurinha com a bandeira da
Alemanha e uma do Brasil. A mesma contagem para as outras duplas (Alemanha-Colômbia e Brasil-Colômbia) nos dará,
neste caso, o número de pacotes procurado:
(5 x 6 – 1) + (5 x 4 – 1) + (6 x 4 - 1) = 29 + 19 + 23 = 71.
Somando os valores obtidos nas três contagens parciais, teremos 120 + 9 + 71 = 200 pacotes distintos.












