Instituto de Fısica Fısica III – 2016/1

Universidade Federal do Rio de Janeiro – Instituto de Fı́sica
Fı́sica III – 2016/1 – Primeira Prova: 16/05/2016
Versão: A
~,
F~e = q E
U = k0
qq ′
,
r
Formulário
I
1
q
~ ·dA
~ = Qint ,
~
,
onde k0 =
E
E = k0 2 r̂
r
4πǫ0
ǫ0
S
~ =E
~ 0 /K ,
E
C = Q/V ,
U=
ǫ0
2
Z
d3 rE 2 ,
~ = −∇V
~ ,
E
1
U = QV ,
2
V = k0
sen2 θ =
q
r
1 − cos 2θ
2
3. Considere um arame fino de comprimento L, disposto
ao longo do eixo Z simetricamente em torno do ponto
z = 0. Neste arame há uma densidade linear de carga
λ = C0 z, onde C0 é uma constante. Encontre a
expressão para o potencial eletrostático num ponto
genérico do plano z = 0 (ou seja, o plano X Y), a
uma distância ρ do arame (supondo que, no infinito,
o potencial se anule).
3/2
i
h
2
−ρ
(a) C0 /(2πǫ0 ) ρ2 + L4
(b)
(c)
(d)
(e)
Seção 1.
(a)
x = v0 t ; y = (1/2)(eVB /mL)t2
(b)
x = (1/2)(eVB /mL)t2 ; y = v0 t
(c)
x = v0 t ; y = v0 t
(d)
x = −v0 t ; y = (1/2)(eVB /mL)t2
(f)
onde θ, é o usual ângulo polar, medido a partir do
eixo X , tal como mostra a figura. Qual é o campo
elétrico no centro do anel?
C0 /(2πǫ0 )[(ρ2 + L2 )3/2 − ρ ]
h
i
1/2
C0 /(2πǫ0 ) ρ2 + L2
−ρ
h
1/2
i
2
C0 /(2πǫ0 ) ρ2 + L4
−ρ
0
Múltipla escolha (8×0,8 = 6,4 pontos)
2. Considere um anel circular, muito fino, de raio a, com
uma carga total Q distribuı́da uniformemente (e estacionariamente) ao longo dele. O anel está no plano
cartesiano x = 0 (ou seja, no plano YZ), com o eixo X
passando pelo centro do anel. Qual é o vetor campo
elétrico num ponto P : (x, 0, 0) situado no eixo X ?
(k0 = 1/4πǫ0 ):
1. Considere que os terminais de uma bateria com uma
d.d.p. conhecida VB estão conectados a duas placas
(planas) condutoras, muito grandes, e perpendiculares
ao eixo Y . As placas não se tocam, e tem uma distribuição superficial de cargas uniforme e estacionária.
Saiba ainda que a placa de menor (maior) potencial
está localizada em y = 0 (y = L). Um elétron com
massa m e carga −e é lançado na região interior às placas, com uma velocidade inicial ~v0 = v0 x̂. A evolução
temporal das coordenadas x(t) e y(t) do elétron dentro
da região limitada pelas placas pode ser dada por:
(e)
5. Considere um anel circular fino, de raio R, com centro
na origem de um sistema de coordenadas cartesianas,
situado no plano z = 0. Tal anel possui uma densidade linear de carga elétrica dada por
λ0 sen θ , se 0 < θ < π ,
λ(θ) =
0,
caso contrário ,
(a)
(b)
(c)
(d)
(e)
x = v0 t ; y = −(1/2)(eVB /mL)t2
x = 1/2(eVB /mL)t2 ; y = −v0 t
(f)
Qx
x̂
(a2 + x2 )3/2
Qx
~ ) = −k0
x̂
E(P
(a2 + x2 )3/2
~ ) = k0 Q x̂
E(P
x2
~ ) = −k0 Q x̂
E(P
x2
Qa
~ ) = k0
(x̂ + ŷ + ẑ)
E(P
(a2 + x2 )3/2
Qa
~ ) = −k0
E(P
(x̂ + ŷ + ẑ)
(a2 + x2 )3/2
~ ) = k0
E(P
(a)
(b)
(c)
4. Uma placa condutora neutra, em equiilı́brio eletrostático, quadrada, de lado L e espessura d, tal que
L ≫ d, é colocada a uma distância 2d de um plano
de cargas também quadrado de lado L, com densidade superficial de cargas dada por σ (σ > 0), como
mostrado na figura abaixo.
(e)
Quais são o módulo E(P ) do campo elétrico no ponto
P localizado entre a placa e o plano, e a densidade superficial de cargas σ(Q), no ponto Q, sobre a superfı́cie
da placa que fica mais próxima do plano?
(a)
(b)
(c)
σ/2ǫ0 ; −σ/2
σ/ǫ0 ; −σ/2
σ/2ǫ0 ; −σ
(d)
σ/ǫ0 ; σ
(e)
−σ/2ǫ0 ; −σ
(f)
(g)
1
(d)
−σ/ǫ0 ; −σ
σ/ǫ0 ; σ/2
2
λ0
ŷ .
8ε0R
λ0
ŷ .
8ε0R
λ0
−
x̂ .
8ε0 R
λ0
x̂ .
8ε0R
~0 .
−
7. Uma partı́cula pontual de carga q > 0 está na presença de uma esfera condutora aterrada. Verifica-se
que o fluxo do campo elétrico através de uma superfı́cie gaussiana S que engloba a partı́cula e a esfera
é q/ε0 (1 − α), com 0 < α < 1. São feitas então as
seguintes afirmativas:
I) Caso a superfı́cie gaussiana envolvesse apenas a esfera condutora, o fluxo obtido seria −αq/ε0 .
II) A carga total induzida na esfera condutora é negativa.
III) A esfera condutora possui uma distribuição de
cargas em sua superfı́cie, porém sua carga total é nula.
IV) A carga total contida dentro da superfı́cie gaussiana S é positiva.
São verdadeiras:
6. Seja um capacitor I ideal, com capacitância CI , de placas planas e paralelas, de mesma área AI e distância LI
entre si, “recheado” com vácuo. Considere, agora, um
novo capacitor II, de placas planas e paralelas, “recheado” com um material isolante de constante dielétrica
K = 2, mas com a distância entre as placas duas vezes maior que a do capacitor I; qual deve ser a nova
área (das placas) para manter a capacitância original
CI ? Considere, a seguir, um terceiro capacitor III, de
placas planas e paralelas, “recheado” com o mesmo
material, mas agora com área (das placas) duas vezes maior que a do capacitor I; qual deve ser a nova
distância entre as placas para manter a capacitância
original CI ?
(a)
AII = 2AI ; LIII = 4LI .
(b)
AII = 4AI ; LIII = 2LI .
(a)
(c)
AII = AI ; LIII = 4LI .
(b)
I, II e IV
(d)
AII = AI ; LIII = 2LI .
(c)
I, III e IV
(e)
AII = 2AI ; LIII = LI /4 .
(d)
III e IV
(e)
I e IV
(f)
AII = AI /2; LIII = LI .
(g)
AII = 2AI ; LIII = LI /2 .
(h)
AII = AI ; LIII = LI .
I e II
com um orifı́cio circular de raio a. A distribuição de carga continua sendo uniforme, com densidade superficial σ.
Para essa nova configuração, responda as perguntas a seguir.
(c) [0,6 ponto] Considere que uma partı́cula de teste, de massa m e carga q0 , onde q0 > 0, tenha sido abandonada
do repouso no ponto P (0, 0, z). Calcule a posição de equilı́brio da partı́cula no eixo Z. Adote a aceleração da
gravidade como ~g = −gẑ.
(d) [0,6 ponto] Calcule a variação da energia potencial eletrostática da partı́cula de carga q0 a partir do momento
em que ela foi abandonada do ponto P (0, 0, z), até passar pela origem do sistema de coordenadas.
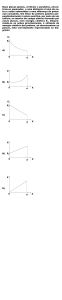
8. Um corpo de dimensões desprezı́veis possui massa m e
carga q. Ele é solto do repouso do alto de uma rampa
de altura h. Nesta região o campo gravitacional g
é constante, e há ainda um campo eletrostático presente. Sabendo-se que o corpo chega ao ponto mais
baixo da rampa com velocidade v, qual a diferença
de potencial eletrostático entre o ponto mais baixo da
rampa e o ponto de soltura do corpo?
(a)
(b)
(c)
(d)
(e)
mv 2 /2q − mgh/q
mv 2 /2q + mgh/q
mgh/q − mv 2 /2q
−mv 2 /2q − mgh/q
Para determinarmos a diferença de potencial
devemos conhecer o formato da rampa.
Seção 2. Questões discursivas (3,6 pontos)
1. [3,6 pontos] Considere uma coroa circular, com uma distribuição superficial de carga σ constante (estacionária e
uniforme), onde σ > 0. A coroa possui raio interno a e raio externo b, e está localizada no plano OX Y, com o seu
centro na origem conforme ilustra a figura abaixo:
(a) [1,2 pontos] Calcule o potencial eletrostático gerado por essa coroa circular no ponto P (0, 0, z), localizado no
eixo Z, conforme ilustra a figura.
(b) [1,2 pontos] Calcule o vetor campo elétrico gerado por essa coroa circular no ponto P (0, 0, z), localizado no eixo
Z, conforme ilustra a figura.
Considere agora o limite em que o raio externo b tende ao infinito, de forma que passamos a ter um plano infinito
3
4
A solução positiva se refere ao caso q0 > 0 e a negativa ao caso q0 < 0.
Gabarito para Versão A
(d) A variação de energia potencial é dada por
Seção 1.
Múltipla escolha (8×0,8 = 6,4 pontos)
1. (a)
5. (a)
2. (a)
6. (c)
3. (e)
7. (b)
4. (a)
8. (c)
∆U = q0 (V (0, 0, 0) − V (0, 0, z)).
Pelo item (a) vemos que
∆U =
No limite em que b → ∞ obtemos
√
√
q0 σ
(b − b2 + z 2 + a2 + z 2 − a).
2ǫ0
(10)
q0 σ √ 2
( a + z 2 − a).
2ǫ0
(11)
∆U =
Seção 2. Questões discursivas (3,6 pontos)
1. Resolução:
(a) O potencial eletrostático de uma distribuição arbitrária num ponto ~rp é dado pela expressão
Z
dq
.
V (~rp ) =
4πǫ0 |~r − ~rp |
(1)
Para a geometria do problema, é conveniente fazermos a integração em coordenadas
p cilı́ndricas. Como se trata de
uma distribuição superficial (uniforme) de carga, temos dq = σdA = 2σπρdρ, r = ρ2 + z 2 e a integral se estende
entre ρ = a e ρ = b. Desta forma temos, no ponto indicado na figura
b2
Z b2
Z b
dy
σ p
σ
σρdρ
p
p
y + z 2 =
=
V (0, 0, z)
=
2ǫ0
ρ2 + z 2
y + z2
a2 2ǫ0 2
a 2ǫ0
a2
√
σ √ 2
=
(2)
[ b + z 2 − a2 + z 2 ] .
2ǫ0
(b) Pela simetria axial, sabemos que o campo deve ter a direção de z. Temos então
~ 0, z) = −∇V
~ = − ∂V (0, 0, z) ẑ .
E(0,
∂z
Sabendo que
temos
∂ √ 2
z
z +C = √
,
∂z
z2 + C
1
σ~z
1
~
√
√
E(0, 0, z) = −
−
2ǫ0
b2 + z 2
a2 + z 2
(3)
(4)
(5)
(c) Na posição de equilı́brio temos que
q0 E = mg .
(6)
Pelo item anterior, no limite b → ∞ o campo de um plano com buraco é dado por
~ 0, z) =
E(0,
σ~z
√
2ǫ0 a2 + z 2
(7)
Substituindo na equação (6) obtemos para a posição de equilı́brio
zeq = ± s
1
mga
q02 σ 2
4ǫ20
(9)
(8)
− m2 g 2
2