Física Geral II

1a LISTA DE EXERCÍCIOS DE TERMODINÂMICA
(incluindo exercícios de revisão de FGE-2001)
Primeira Parte: Exercícios de revisão FGE 2001 (optativo)
1. O processo de calibração de um termômetro de gás a volume constante consiste em
medirmos os valores de pressão para os pontos de gelo (pg) e vapor (pv). Repetem-se então
estas medidas, reduzindo-se gradativamente a pressão dentro do bulbo do termômetro,
mantendo sempre o volume constante. Se fizermos agora um gráfico da razão (pv /pg)V ( o
índice V significa que o volume é mantido constante), observamos experimentalmente que a
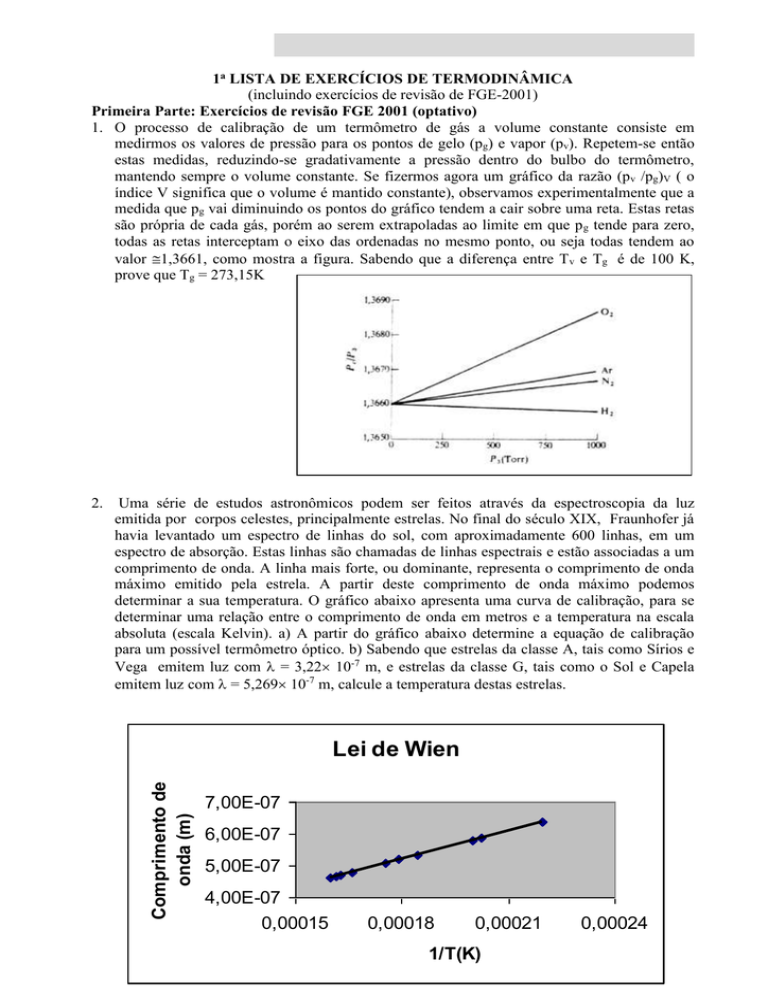
medida que pg vai diminuindo os pontos do gráfico tendem a cair sobre uma reta. Estas retas
são própria de cada gás, porém ao serem extrapoladas ao limite em que p g tende para zero,
todas as retas interceptam o eixo das ordenadas no mesmo ponto, ou seja todas tendem ao
valor 1,3661, como mostra a figura. Sabendo que a diferença entre T v e Tg é de 100 K,
prove que Tg = 273,15K
Uma série de estudos astronômicos podem ser feitos através da espectroscopia da luz
emitida por corpos celestes, principalmente estrelas. No final do século XIX, Fraunhofer já
havia levantado um espectro de linhas do sol, com aproximadamente 600 linhas, em um
espectro de absorção. Estas linhas são chamadas de linhas espectrais e estão associadas a um
comprimento de onda. A linha mais forte, ou dominante, representa o comprimento de onda
máximo emitido pela estrela. A partir deste comprimento de onda máximo podemos
determinar a sua temperatura. O gráfico abaixo apresenta uma curva de calibração, para se
determinar uma relação entre o comprimento de onda em metros e a temperatura na escala
absoluta (escala Kelvin). a) A partir do gráfico abaixo determine a equação de calibração
para um possível termômetro óptico. b) Sabendo que estrelas da classe A, tais como Sírios e
Vega emitem luz com  = 3,22 10-7 m, e estrelas da classe G, tais como o Sol e Capela
emitem luz com  = 5,269 10-7 m, calcule a temperatura destas estrelas.
Lei de Wien
Comprimento de
onda (m)
2.
7,00E-07
6,00E-07
5,00E-07
4,00E-07
0,00015
0,00018
0,00021
1/T(K)
0,00024
3. A massa específica do ar a 0 0C é 1,29 g/l, o volume molar é 22,4 l/mol e a velocidade do
som é 332 m/s. Calcule a razão entre os calores específicos e o calor específico molar a
volume constante. Supondo que o ar seja composto unicamente de oxigênio, a que freqüência
o comprimento de onda do som será igual ao livre caminho médio do oxigênio ( Considere o
diâmetro da molécula de oxigênio 1gual a 3,0 x 108 cm)
4. Um sistema termodinâmico é levado de um estado inicial A para um estado B, passa pelo
estado C e depois volta ao estado A, segundo o ciclo mostrado abaixo. Calcule o trabalho
realizado pelo sistema em cada uma das etapas, inclusive o trabalho total. Sabendo que nos
trechos AB e BC são fornecidos respectivamente 7,0 J e 8,0 J, determine o calor total
fornecido ou retirado do sistema no trecho CA.
5. Uma dado sistema é tal que uma variação quase estática no volume a N = cte pode ser
5
3
descrita pela seguinte equação de estado p  V , na qual  é uma constante que deve ser
determinada a partir do gráfico. a)Calcule o trabalho quase-estáticon sobre o0 sistema e o
fluxo líquido de calor para o sistema em cada um dos três processos ( ADB, ACB, e no
processo linear AB), como mostrado na figura. Descreva, segundo o gráfico, o que acontece
com o gás em cada um dos três caminhos. (ver Callen pág 21).
6. Um anel de cobre de 20,0 g tem um diâmetro de 3,00 cm à temperatura de 0 0C, uma esfera
de Alumínio tem diâmetro de 3,00600 cm à temperatura de 100 0C. A esfera é colocada em
cima do anel e permite-se que os dois encontrem seu equilíbrio térmico, sem ser perdido
calor para o ambiente. A esfera passa exatamente pelo anel na temperatura de equilíbrio.
Qual a temperatura de equilíbrio e a massa da esfera? Calcule a variação da entropia do
sistema. Cu=17 x 10-6 0C-1, Al=23 x 10-6 0C-1 e cCu = 0,0923 cal/g0C cAl = 0,215 cal/g0C
7. Mistura-se 800 g de gelo a – 40 0C com 500 g de água a 0 0C. Calcule a temperatura final do
sistema e a massa de água ao final do processo. Considere Lliq = 79,5 cal/g, cágua = 1,0
cal/g0C e cgelo = 0,5 cal/g0C.
8. Um mole de um gás ideal passa por uma expansão isotérmica. Partindo da 10 lei da
Termodinâmica, encontre o calor adicionado ao gás em termos dos volumes final e inicial e
da temperatura
9. Mostre que a variação de pressão na atmosfera da terra, suposta isotérmica, é dada por
p  p0 e Mgy / RT , onde M é a massa molecular do ar.
10. Um gás ideal sofre uma compressão adiabática de p = 1,0 atm, V = 1,0 x 106 L, T = 0,0 0 C
para p = 1,0 x 105 atm, V = 1,0 x 103 L. a) Este gás é mono, di ou poliatômico? b) Qual a sua
temperatura final? c) Quantos moles do gás estão presentes? d) Qual a energia cinética
translacional total por mole antes e depois da compressão?
Segunda Parte: Exercícios dos caps 1 e 2
11. Faça uma análise de um sistema termodinâmico segundo os seguintes aspectos: estados e
propriedades, parâmetros que caracterizam o sistema e as condições de equilíbrio.
12. (a) Diga como um sistema, contendo dois gases, pode estar em equilíbrio mecânico, mas
não em equilíbrio térmico ou químico. (b) Diga como um sistema contendo dois gases
pode estar em equilíbrio térmico, mas não em equilíbrio mecânico ou químico. (c) Diga
como um sistema, contendo dois gases, pode estar em equilíbrio térmico e mecânico, e
não em equilíbrio químico.
13. Em um gráfico de volume contra temperatura, desenhe e designe linhas indicando os
seguintes processos, cada um iniciando pelo mesmo estado T0 e V0: (a) uma expansão
isotérmica; (b) uma compressão isotérmica; (c) um aumento de temperatura isocorico.
14. A pressão de um gás ideal mantido a volume constante é dada pela equação P = AT onde
T é a temperatura termodinâmica e A é uma constante. Seja a temperatura T* definida por
T* =B1nCT onde B e C são constantes. A pressão P é 0,1 atm no ponto tríplice da água.
A temperatura T* é 0 no ponto tríplice e 100 no ponto de vapor. (a) Encontre os valores
de A, B e C. (b) Encontre o valor de T*, quando P é 0,15 atm. (c) Encontre o valor de P,
quando T* é 50. (d) Qual é o valor de T* no zero absoluto? (e) Esboce um gráfico de T*
contra a temperatura Celsius t para —2000C < t < 2000C.
15. Estime, tão acuradamente quanto puder, da Fig. 2.1, o volume específico molar do co 2 à
pressão de 3 x 10~ N m2 e à temperatura T1. Suponha T, = 340K. (b) A esta pressão e
temperatura, quantos quilomoles de CO2 estarão contidos em um tanque de volume 0.5
m3? (c) Quantos quilomoles o tanque iria conter, se o CO2 fosse um gás ideal?
16. A Fig. 2.20 mostra cinco processos, a - b, b - c, c - d, d - a e a - c, em um gráfico no plano
P-v para um gás ideal em um sistema fechado. Mostre os mesmos processos (a) no plano
P-T e (b) no plano T-v. (c) Localize os quatro pontos de interseção das linhas na
superfície P-v-T da Fig. 2.2, que correspondem aos pontos a, b, c, d da Fig. 2.20
17. Na Fig. 2.20, seja P2 = 10 x 105 N m-2, P1 = 4 x 105 N m-2, v1 = 2,5 m3 quilomol-1.
Encontre (a) a temperatura T, (b) o volume específico v2 (c) a temperatura nos pontos b e
d o volume v no ponto a se o sistema consistir de 4 quilomoles de hidrogênio, (e) a massa
do hidrogênio.
18. Em todos os chamados gases diatômicos, algumas das moléculas estão dissociadas em
átomos separados, a fração dissociada aumentando com a temperatura. O gás como um
todo consiste, então, em uma porção diatômica e outra monoatômica. Muito embora cada
componente possa atuar como um gás ideal, a mistura não o é, porque o número de moles
varia com a temperatura. O grau de dissociação δ de um gás diatômico é definido como a
razão da massa m1 da porção monoatômica para a massa total m do sistema: δ = m1/m.(a)
Mostre que a equação de estado do gás é PV = (δ + 1)(m/M2)RT, onde M2, é o “peso”
molecular da componente diatômica. Suponha que o gás obedeça à lei de Dalton (P = P A
+ PB). (b) A tabela abaixo dá uma lista de valores medidos da razão PV/m para vapor
iodado a três temperaturas diferentes. Calcule e mostre, em um gráfico, o grau de
dissociação como função da temperatura.
t(0C)
800
1.000
1.200
PV/m (Jkg-1) 3,72 x 104 5,08 x 104 7,30 x 104
19. a)
Mostre que o coeficiente de dilatação volumétrica pode ser expresso
1   
como     ,onde ρ é a densidade. (b) Mostre que o coeficiente de compressão
  T  p
1   
 
  P T
20. a) Mostre que o coeficiente de dilatação de um gás de Van der Waals é:
Rv 2 v  b 
, e qual será a expressão para β se a = b = 0 (gás ideal)? b) Mostre

2
RTv 3  2av  b 
isotérmica pode ser expresso como:  
que o coeficiente de compressão de um gás de Van der Waals é:  
v 2 v  b 
2
RTv 3  2av  b 
2
,
e qual será a expressão para κ se a = b = 0?
21. Uma substância hipotética tem um coeficiente de compressão isotérmica κ = a/v, e um
coeficiente de dilatação β= 2bTIv, onde a e b são constantes. (a) Mostre que a equação de
estado é dada por v — bT2 + aP = constante. (b) Se a uma pressão P0 e temperatura T0, o
volume específico é v0, avalie a constante.
22. Uma substância tem um coeficiente de compressão isotérmica κ = aT3/P2, e um
coeficiente de dilatação β = bT2/P, onde a e b são constantes. Encontre a equação de
estado da substância e a razão a/b.
23. A relação entre a pressão, temperatura e o volume (v) de 1 mol de hidrogênio pode ser
dada pela equação de estado P  RT v  B(T ) , na qual B independe de P. a) encontre
 v 
 v 
  e   , e expresse dv como função de T e P, assim como feito em aula. b)
 T  P  P  T
prove que dv é uma diferencial exata. c) confirme a equação
 P 
 V   P 
   
 
 usando a equação de estado acima.
 T V
 T  P  V  T
 V 
24. O volume de um cilindro circular é dado pela expressão V   r 2 h . Encontre 
 e
 r h
 V 

 . Escreva a diferencial completa dV , e verifique que é uma diferencial exata.
 h r
25. Um volume V à temperatura T contem nA moles de um gás ideal A e nB moles de um gás
ideal B. Estes gases não reagem quimicamente. a)Mostre que a pressão total P é dada
por: P  pA  pB , na qual pA e pB são as pressões parciais de cada gás. b) Mostre que
nA
é a fração de moles de A no sistema.
pA  xA P , na qual xA 
nA  nB
26. Uma equação de estado aproximada é P  v  b   RT . a) Calcule os coeficientes de
dilatação e de compressão para uma substância que obedeça esta equação de estado. b)
Mostre que as equações correspondente para um gás de Van der Waals se reduzem as
expressões derivadas em (a) quando a = 0.
27. Mostre que as constantes críticas de uma substância que obedece à equação de estado:
P  v  b  e à / vRT   RT , são Pc  a / 4e 2b 2 , vc  2b , Tc  a / Rb .
28. Faça os seguintes programas no Maple ou Matemática (em anexo).