III

Mecânica dos Fluidos I
Aula 3
Turma 3305
Prof. António Sarmento
Tel. 21 8417405
Email: [email protected]
I
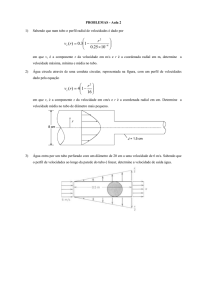
Água escoa-se num tubo de secção circular constante de raio R=10 cm. Admita que o fluido
tem apenas velocidade axial e que tem um perfil de velocidades uniforme (isto é, que é
constante em toda a secção).
A. Calcule:
1. O caudal volúmico;
2. O caudal mássico;
3. O caudal de energia cinética;
4. O caudal de quantidade de movimento.
B. Reconheça que o cálculo que efectuou resultou da aplicação da equação genérica

q B    V .n dS
 
A
que dá caudal qB de uma grandeza B cujo valor por unidade de volume seja .
Nota: O caudal de uma dada grandeza representa o valor dessa grandeza que atravessa a
superfície em questão por unidade de tempo.
Problema 3.5
Água escoa-se num tubo de secção circular constante de raio R=10 cm. Admita que o fluido
tem apenas velocidade axial e que o perfil de velocidades depende apenas da distância r ao
eixo do tubo (perfil com simetria axial).
a) Calcule o caudal volúmico, o caudal mássico, o caudal de energia cinética e o caudal
de quantidade de movimento para as seguintes distribuições radiais de velocidade
axial:
1. Perfil de velocidades parabólico
  r 2 
v z r   V0 1    
  R  
com V0=2 m/s.
2. Perfil de velocidades experimental
r (cm)
0
2
4
5
6
7
8
9
vz(r) [m/s]
2
1,92
1,68
1,5
1,28
1,02
0,72
0,38
b) Calcule a velocidade média na secção
Notas:
1. O perfil parabólico ocorre na ausência de turbulência, quando o escoamento é dito de
laminar;
2. Pode simplificar a equação genérica para o cálculo de caudal de uma grandeza B
dada no problema anterior sabendo que as propriedades do escoamento não variam
com  mas apenas com o raio r e que o elemento de área num sistema de
coordenadas cilíndrico é dado por dS  rdrd .
3. Pela condição de não-escorregamento a velocidade do fluido na parede do tubo é
nula, vz(r=R)=0.
4. Define-se a velocidade média como sendo <V>=q/A, isto é, a velocidade do
escoamento tampão que transporta o mesmo caudal.
II
Um jacto de água cilíndrico com uma secção transversal A=3 cm2 e uma velocidade V=10
m/s incide normalmente numa placa, saindo desta com uma direcção tangencial à placa.
Tenha em atenção que a velocidade do jacto de água que abandona a placa é idêntica à
velocidade do jacto e que a pressão exterior é atmosférica e que se exerce em toda a fronteira
entre o ar e o jacto. Admita que o perfil de velocidades é tampão nas secções em que o jacto
abandona a placa.
V=10 m/s
V=10 m/s
V=10 m/s
a) Determine a força que se exerce sobre o jacto.
b) Determine a força que o jacto exerce sobre a placa.
Passos para a resolução:
1. Anteveja em que direcções são diferentes de zero as forças solicitadas.
2. Estabeleça o princípio de conservação que permite responder a este problema.
3. Passe a equação o enunciado do princípio que estabeleceu e resolva-a.
4. Reflicta sobre se todas as forças aplicadas ao jacto são produzidas pela placa.
III
Uma tubagem com uma área transversal constante A= 5 cm2 por onde passa um caudal de
água de q=10 l/s contém um cotovelo como o representado na figura. Sabendo que se
mediram as pressões absolutas p1=115 kPa e p2=105 kPa, nas secções das flanges de ligação
do cotovelo ao resto da tubagem, determine a força total que se exerce nos parafusos das
flanges. Admita que o perfil de velocidades é tampão nas secções referidas onde se mediu a
pressão.
1
y
x
2
Passos para a resolução:
1. Anteveja em que direcções é diferente de zero a força solicitada.
2. Estabeleça o princípio de conservação que permite responder a este problema.
3. Passe a equação o enunciado do princípio que estabeleceu e resolva-a.
4. Reflicta sobre se todas as forças aplicadas ao jacto são produzidas pelo cotovelo.