Problemas Resolvidos de Física

Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
HALLIDAY, RESNICK, WALKER, FUNDAMENTOS DE FÍSICA, 8.ED., LTC, RIO DE
JANEIRO, 2008.
FÍSICA 1
CAPÍTULO 4 – MOVIMENTO EM DUAS E TRÊS DIMENSÕES
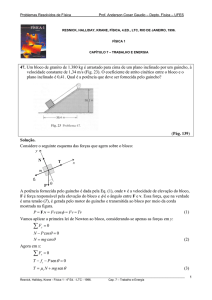
131. Um golfista arremessa uma bola a partir de uma elevação imprimindo à bola uma velocidade
inicial de 43 m/s e um ângulo de 30o acima da horizontal. A bola atinge o campo a uma
distância horizontal de 180 m do local de lançamento. Suponha que o campo seja plano. (a)
Qual era a altura da elevação de onde foi arremessada a bola? (b) Qual era a velocidade da bola
ao chegar ao campo?
(Pág. 94)
Solução.
Considere o seguinte esquema da situação:
y
v0
θ0
h
x
d
(a) Para determinar a altura da elevação, vamos resolver as equações de movimento em x e em y. O
movimento da bola em x ocorre com velocidade constante:
x = x0 + v x 0t
d = 0 + v0 cos θ 0 t
t=
d
v0 cos θ 0
(1)
O movimento em y ocorre com aceleração constante −g:
1
y − y0 = v y 0 t − gt 2
2
1
0 − h = v0 sen θ 0 t − gt 2
2
Substituindo-se (1) em (2):
⎛
d
− h = v0 sen θ 0 ⎜
⎝ v0 cos θ 0
⎞ 1 ⎛
⎞
d
⎟− g⎜
⎟
⎠ 2 ⎝ v0 cos θ 0 ⎠
(
)
(2)
2
9,8 m/s 2 (180 m )
gd 2
h= 2
− d tan θ 0 =
− (180 m ) tan 30D = 10, 5604 " m
2
2
D
2v0 cos 2 θ 0
2 ( 43 m/s ) cos 30
2
( )
( )
h ≈ 11 m
(b) O módulo da velocidade da bola imediatamente antes de atingir o solo, v, é dada por:
________________________________________________________________________________________________________
a
Halliday, Resnick, Walker - Fund.de Física 1 - 8 Ed. - LTC - 2009.
Cap. 04 – Movimento em Duas e Três Dimensões
1
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
v = v x2 + v y2
(3)
Como o componente da velocidade em x é constante, temos:
( )
v x = v x 0 = v0 cos θ = ( 43 m/s ) cos 30D = 37, 2390 " m/s
O componente y da velocidade pode ser calculado por meio da análise do movimento em y:
v y2 = v y20 − 2 g ( y − y0 )
v y2 = v02 sen 2 θ − 2 g ( 0 − h )
v y = v02 sen 2 θ + 2 gh =
( 43 m/s )
2
( ) (
)
sen 2 30D + 2 9,8 m/s 2 (10, 5604 " m ) = 25,8695" m
Substituindo-se os valores de vx e vy em (1):
v=
( 37, 2390" m/s )
2
+ ( 25,8695" m ) = 45, 3429 " m/s
v ≈ 45 m/s
________________________________________________________________________________________________________
a
Halliday, Resnick, Walker - Fund.de Física 1 - 8 Ed. - LTC - 2009.
Cap. 04 – Movimento em Duas e Três Dimensões
2