Exercícios Logaritmo

WWW.CURSOSMIGUEL.COM.BR
Matemática – Caderno 5
FUNÇÃO LOGARÍTMICA:
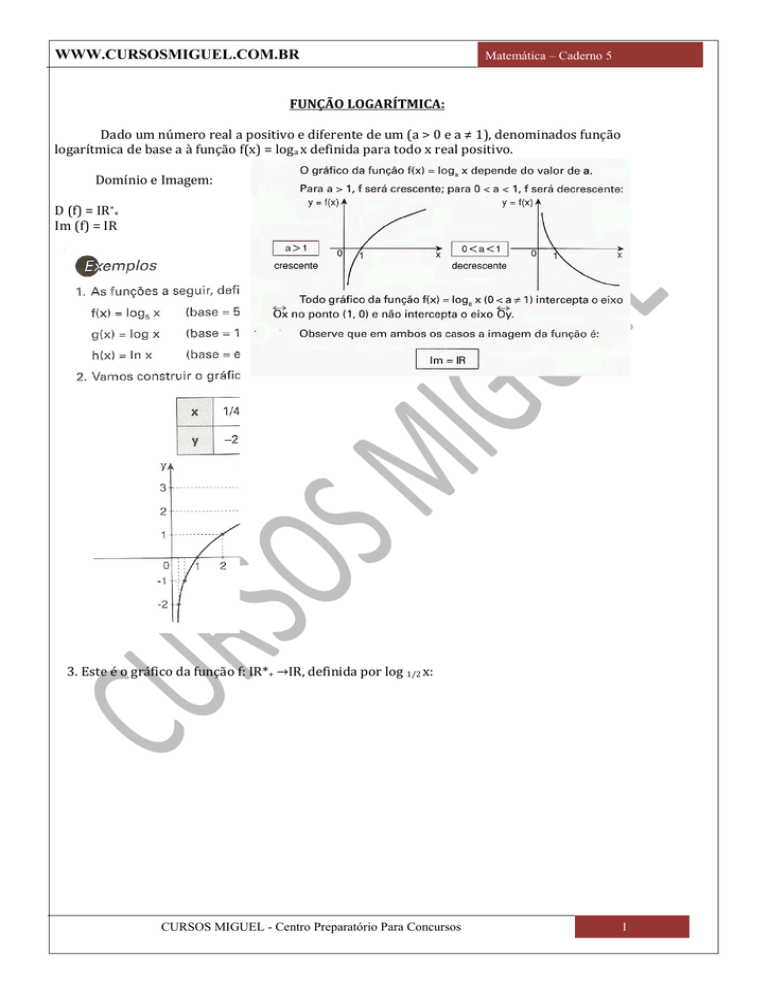
Dado um número real a positivo e diferente de um (a > 0 e a ≠ 1), denominados função
logarítmica de base a à função f(x) = loga x definida para todo x real positivo.
Domínio e Imagem:
2
D (f) = IR*+
Im (f) = IR
3. Este é o gráfico da função f: IR*+ →IR, definida por log 1/2 x:
CURSOS MIGUEL - Centro Preparatório Para Concursos
1
WWW.CURSOSMIGUEL.COM.BR
Matemática – Caderno 5
PROPRIEDADES DOS LOGARITMOS
log a b = x
↔ b = ax
NOMENCLATURA
Potenciação
base
potência
expoente
Elementos/ Operação
a
b
x
Logaritmação
base do logaritmo
logaritmando
Logaritmo
P1. log b (a.c) = log b a + log b c
P2. log b
= log b
a - log b c
= . log b a
P3. log b √ = log b
P4. log b an = n. log b a
=b
P5.
P6.
log a 1 = 0
P7.
log a a = 1
P8.
log a am = m
P9.
log b x = log b y ↔ x = y , ∀ (x,y,b)  IR* + , e b≠ 1
Cologaritmo de um número
colog a b = - log a b = log a
1
b
Mudança de base
log a b =
consequências → log a b . log b a = 1 e
log a b. log c a = log c b
Equações logarítmicas
Equações com logaritmos, em que as variáveis podem aparecer no logaritmando ou na base, são
chamadas equações logarítmicas.
CURSOS MIGUEL - Centro Preparatório Para Concursos
2
WWW.CURSOSMIGUEL.COM.BR
Matemática – Caderno 5
Para resolvê-las, aplicamos a definição, as condições de existência e as propriedades dos
logaritmos.
Exemplos:
Resolva em IR as equações:
a) log x (2x + 15) = 2
b) log 2 (2x +3) = log 2 x2
Exercícios 1
01. O logaritmo de um certo número numa certa base é 3. O logaritmo desse mesmo número numa base
igual a metade da anterior é 6. Determinar o número procurado.
02. A solução da equação
√
=
é um número k. Determine o logaritmo de k na
base √ .
03. Calcule o valor da expressão log 1/2 32 + log10 0,001 – log 0,1
√
.
04.(Mús/Saúde) Sabendo que log P = 3Log a – 4Log b + log c, assinale a alternativa que representa
o valor de P. (dados: a = 4,
b = 2 e c = 16)
a) 1 2
b) 5 2
c) 1 6
d) 2 4
e) 73
05. Resolva a equação log2 (x + 2) + log2 (x - 2) = 5
06. Resolva a equação log2 (x – 1) + 1 = log2 (x + 2) + log2 (7 - x) - log2 3
07. (URI) Considere a expressão A = - log 0,1√
08. Sabendo que log b a = 4 , calcular
- (- log
+ log 6 36). O valor de A é:
b6 .
09. Resolva a equação: log 5 x + log 25 x = 3
10. Sendo log x a = 6 , e log x b = 4 e log x c = 2, calcular log c
a.b.c .
CURSOS MIGUEL - Centro Preparatório Para Concursos
3
WWW.CURSOSMIGUEL.COM.BR
Matemática – Caderno 5
11. Calcule o valor de x em cada uma das equações:
a) log 2 (3x – 1) + log 2 x = 2
b) log 3 (x2 – x – 6) = log 3 4 + log 3 ( x – 3)
c) log 16 x + log 4 x + log 2 x = 7
d) log 1/3 (x + 2) + log 3 (2x – 1) = 0
Gab: 1)64
9) 25
2)8
10) 3
3)-13/2
4)
11)a.1
b.{}
5)6
c.16
6)4
7) -7/6
8)3/4
d.3
Exercícios 2
01. (PUC) Se log
2 2
512 = x, então x vale:
a) 6
b) 3/2
c)9
d)3
e)2/3
02. (UFRGS) O valor de log 3 18 + log 3 6 - log 3 12 é:
a) 1
b)2
c)12
d)
log 324
log 312
e) log 312
03. (UFRGS) Se log a = 4, então log
a
é:
1000
a) 2
b) 1
c) 0
d) -1
e) -2
04. (UFSM) Se log 5 = a e log 7 = b, então log 122,5 é:
a) a + b
b) a + b + 1
c) a + b – 1
d) 2a + 2b -1
e) 2a + 2b
CURSOS MIGUEL - Centro Preparatório Para Concursos
4
WWW.CURSOSMIGUEL.COM.BR
Matemática – Caderno 5
05. (PEIES) Supondo satisfeitas as condições de existência dos logaritmos e sendo log c a = b e log c d =
2, a expressão
a
é equivalente a:
dc
b 1
2 2
b 1
4 2
b 3
4 2
b
+1
4
b 3
2 2
log d
a)
b)
c)
d)
e)
4 log x 3  3 log x 2  2 log x
06. (UFSM) Se x  IR e x > 1 , então a expressão y =
é equivalente
4 log x 5  4 log x 4  2 log x 2
a) 9/10
b)15/21
c) 1/2
d) -20 log x
e) 1
log3 2
07. (PUC) A potência 9
é igual a:
a) 2
b) 3
c) 4
d) 5
e) 6
08. (PUC) Se log 2 m = k, então log 8 m será:
a) 2k
b) k/3
c) 3k
d) k/2
e) k + 6
09. (PEIES) Sabendo que log 10 3 = 0,4771 e log 10 6 = 0,7781, a solução da equação 10x = 9.16 é:
a) 1,5128
b) 2,5128
c) 2,8215
d) 2,1582
e) 1,1582
10. (PUC-RS) Na igualdade x = 7
a) 7
b) 10
c) 14
d) 35
e) 49
log7 5  log7 2
, o valor de x é:
11. (UFSM) Se log m = 2 – log 4, então m é:
a) 0,04
b) 1,5
c) 20
d) 25
e) 96
CURSOS MIGUEL - Centro Preparatório Para Concursos
5
WWW.CURSOSMIGUEL.COM.BR
Matemática – Caderno 5
12. (UFSM) O valor de log 3 4 x log 4 5 x log 5 27 é:
a) 1/5
b) 1/4
c) 1/3
d) 2
e) 3
13. (UFRGS) O valor de log (217,2) – log (21,72) é:
a) -1
b) 0
c) 1
d) log (217,2 – 21,72)
e)
log ( 217,2)
log( 21,72)
14. (UFRGS) O logaritmo de um número na base 16 é 3/2. Então, o logaritmo deste número na base 1/4
é:
a) -4/3
b) -3/4
c) 3/8
d) -3
e) 6
15. (EsPCEx). Na figura abaixo, está representado o gráfico da função y=log x. Nesta representação estão
destacados três retângulos cuja soma das áreas é Igual a:
a) log2 + log3 + log5
b)log30
c) 1+log30
d) 1 + 2log 30
e) 1 + 2log15
16. (UFSM) Seja k a solução da equação log 4 (log 2 x) = -1. O valor de k4 é :
a) 1/8
b) 1/2
c) 1
d) 4
e) 2
17. (UPF) A expressão
a)
1
1
+ log   é igual a:
log x
x
1
1  log 2 x
1  log 2 x
log x
1  log 2 x
c)
log x
b)
CURSOS MIGUEL - Centro Preparatório Para Concursos
6
WWW.CURSOSMIGUEL.COM.BR
d)
Matemática – Caderno 5
1
2 log x 2
e) – log x2
18. (EsPCEx) A figura abaixo fornece a representação gráfica da função y = log b x
y
0.25
1
x

-1
Nestas condições, o valor de b é:
a) 1/4
b) 2
c) 3
d) 4
e) 10
19. (UNICRUZ) Dados log 2 = a e log 3 = b , encontrar o valor de log 15 = ?.
a) a + b
b) a + b + 1
c) a – b + 1
d) a – b – 1
e) 1 – a + b
20. (EsPCEX) Seja
O conjunto solução da desigualdade
( ) no intervalo [
a) [0, ).
b) *
+
, é igual a:
c) [
.
d) [
e) [
).
)
 1 x 
 tem por domínio:
x

2


22. (EsPCEx) A função f x   log
a)   2, 1
b)     2
c)     2, 1
3
2
d)   ,  2 1,  
4
3
5
4
e) 
 n 
 , em que n é um
 n 1
23. (EsPCEx) Considere a soma S = log    log    log    ...  log
numero natural. O menor valor de n para o qual S > 1 é:
a) 20
b) 21
c) 22
d) 25
e) 29
24. (EsPCEx) Há números reais para os quais o quadrado de seu logaritmo decimal é igual ao logaritmo
decimal de seu quadrado. A soma dos números que satisfazem essa igualdade é:
a) 90
b) 99
c) 100
d) 101
e) 201
25. (ESPCEx) Acrescentando 48 unidades a um numero, seu logaritmo na base 5 aumenta de 2
unidades. Esse número é:
a) 1
b) 2
c) 3
d) 6
e) 12
CURSOS MIGUEL - Centro Preparatório Para Concursos
7
WWW.CURSOSMIGUEL.COM.BR
Matemática – Caderno 5
26. (EsPCEx) Um satélite será levado ao espaço por um foguete que tem seu consumo de combustível
calculado pela função C(t) = log2(t2 + 7)2 + 2 log2
1
, em que C é o consumo em toneladas e t é o tempo
7
em horas. Para colocar o satélite em órbita, o foguete deverá percorrer uma distância de 56.000Km a
uma velocidade média de 8.000Km/h.
Com base nessas informações, o físico responsável pelo cálculo chegou a conclusão de que o foguete,
para cumprir a missão, terá um consumo de combustível igual a:
a) 1 tonelada
d) 7 toneladas
b) 2 toneladas
e) 8 toneladas
c) 6 toneladas
27. (EsPCEx) A curva da figura representa o gráfico da função f(x) = log2x.
Dados log102 = 0,30 e log1012 = 1,08.
Com base nesses dados, as somas das áreas dos dois retângulos hachurados é, aproximadamente,
a) 1,60
b) 2,10
c) 2,08
d) 2,60
e) 3,60
28 – (EsPCEx) A figura abaixo representa o gráfico f :      tal que f(x) = log a x,
onde a > 1.
Estão locados no gráfico os logaritmos de três abscissas: “a” (que é a própria base), “b” e “c”. Sabendo
que OA = BC , podemos afirmar que
a) log a b = c
b) a c = b
c) a.b = c
d) a + b = c
e) 10 a + 10b = 10c
29. (EEAR) Se x e y são números reais positivos, co
= x, e
256 = 4, então x + y é igual a
a) 2
b) 4
c) 7
d) 9
e)12
30. (EEAR) Sejam x, y e b números reais maiores que 1. Se
x=2e
y = 3, então o valor de
(x² y³) é
a) 13
b) 11
c) 10
d) 8
e) 15
CURSOS MIGUEL - Centro Preparatório Para Concursos
8
WWW.CURSOSMIGUEL.COM.BR
Matemática – Caderno 5
31. Os pontos 0, 3 e 1, 5 pertencem ao gráfico da função f x   2 x b  c, onde b e c são naturais.
1
b  2c é:
2
3
b) 
c) 2
2
Então o valor de
3
2
a)
d)
5
2
32. Se loga 2 = M e loga 3 = N, então loga 12 é:
a) 2M + N b) M² + N c) M²N d) 2MN
e) 0
e) Nda
33. Se log3 4 = a e log4 5 = b, então o valor de log3 5 em função de a e b é:
a)
1
ab
b)
b
a
c)
1
ab
d) a.b
e)
a
b
34. Sejam x, y e b números reais maiores que 1. Se
(x² y³) é
a) 13
b) 11
c) 10
x=2e
y = 3, então o valor de
d) 8
35. A razão entre o logaritmo de 16 e o de 4, numa mesma base b, sendo 0 < b ≠ 1, é
a) 1/4.
b) 1/2.
c) 4.
d) 2
36. Considerando n > 1, se log a n = n, então o valor de a é
a) n
b) nn
c)
d)
37. (EsSA) O logaritmo de um produto de dois fatores é igual à soma dos logaritmos de cada fator,
mantendo-se a mesma base. Identifique a alternativa que representa a propriedade do logaritmo
anunciada.
a) logb (a.c) = log b a + log b c
b) logb (a.c) = log b (a +c)
c) logb (a+ c) = (log b a) . (log b c)
d) logb (a+ c) = log b (a.c)
e) loge (a.c) = log b a + log f c
38. (EsSA) Sabe-se que 1, a e b são raízes do polinômio p(x) = x³ - 11x² + 26x – 16, e que a > b. Nessas
condições, o valor de ab + log b a é
a) 49/3
b) 67
c) 193/3
d) 19
e) 64
39. (EsSA) Aumentando-se um número x em 75 unidades, seu logaritmo na base 4 aumenta em 2
unidades. Pode-se afirmar que x é um número
a) irracional
b) maior que 4
c) divisor de 8 d) menor que 1 e) múltiplo de 3
40. (EsSA) Se f(x) =
a)
b)
√
, com x real e maior que zero, qual o valor de f(f(5))?
c)
41. (EsSA) Se 5 x +2 = 100 então 52x é igual a:
a) 16
b) 100
c) 8
d) 10
d)
e)
e) 4
CURSOS MIGUEL - Centro Preparatório Para Concursos
9
WWW.CURSOSMIGUEL.COM.BR
Matemática – Caderno 5
42. (EsSA) Se log 2 3 = a e log 2 5 =b Então o valor de log 0,5 75 é:
a) a – 2b
b) –a – 2b
c) -a +2 b
d) a - b
e) a + b
43.( Mús/Saúde) O conjunto solução da equação exponencial 4x-2x = 56 é
a) { - 7 , 8 }
b) { 3 , 8 }
c) { 3 }
d) { 2 , 3 }
e) {8}
44. (UFRGS) Aproximadamente
a) 109 e 1010.
b) 1010 e 1011.
c) 1011 e 1012.
d) 1012 e 1013.
e) 1013 e 1014.
45. (UFRGS) O número
a) 0 e 1
b) 1 e 2
c) 2 e 3
d) 3 e 4
e) 4 e 5
por 0,301, verificamos que o número 1610 está entre:
está entre:
46. (UFSM) Suponha que um campo de futebol seja colocado em um sistema cartesiano ortogonal,
conforme mostra a figura.
Para que o ponto A (log10 (x + 1) + 1, log10 (x2 + 35)) tenha abscissa e ordenada iguais, é necessário e
suficiente que
a) x > -1.
b) x = 5.
c) x < -1.
d) x = -5.
e) x > 5.
47. (EsSA) Dados log 3 = a e log 2 = b , a solução de 4x=30 é
a) (2a+1)/b
b) (a+2)/b
c) (2b+1)/a
48. Se o gráfico da função f(x) = log b x passa pelo ponto (
a:
a) 3
b) 2
x
c)
x
d) (a+1)/2b
e) (b+2)/a
), então o valor da expressão
d) -
x
49. (UPF) Dado loga = 2 , logb = 3 e log c
a) 20/32
b) 30/31
c) 8
é igual
e) -4
= 5 , então podemos dizer que log abcx vale:
d) 14/25
CURSOS MIGUEL - Centro Preparatório Para Concursos
e) 25
10
WWW.CURSOSMIGUEL.COM.BR
Matemática – Caderno 5
50. (EsPCEx) Um dos modelos matemáticos de crescimento populacional é conhecido como “Modelo
Malthusiano” (Thomas Malthus, 1766-1834). Neste modelo, a evolução de uma população é dada pela
função P(t) = Po. Kt em que Po é a população inicial, k indica a taxa de crescimento (considerada constante e
não negativa neste modelo) e t é o tempo decorrido.
Um biólogo que estudava uma cultura de bactérias observou que, oito horas após o início do experimento,
a população era de 8000 indivíduos e que, duas horas depois dessa observação, a população era de 16000
indivíduos. Podemos afirmar que a população inicial era de:
a) 250.
b) 500.
c) 512.
d) 1000.
e)1024.
51. (EsPCEx) O número N de bactérias de uma cultura é dado em função do tempo t (em minutos), pela
fórmula N(t)=(2,5)1,2t. Considere log10 2=0,3, o tempo (em minutos) necessário para que a cultura tenha
1084 bactérias é:
a) 120
b) 150
c) 175
d)185
e)205
Y
52. Daqui a y anos o valor de uma motocicleta será de V = 2000.(0,75) dólares. A partir de hoje, daqui a
quantos anos ela valerá a metade do que vale hoje? (Adote log 2 = 0,3 e log 3 = 0,48)
a) 3 anos
b) 2,5 anos
c) 2 anos
d) 4,5 anos
e) 6 anos
53. (EsSA). Utilizando os valores aproximados log 2 = 0,30 e log 3 = 0,48, encontramos para log √
de:
a) 0,32
b) 0,35
c) 0,31
d) 0,33
e) 0,36
o valor
Gabarito: 1)a 2)b 3)d 4)d 5)c 6)c 7)c 8)b 9)d 10)b 11)d 12)e 13)c 14)d 15)e 16)e 17)b 18)d 19)e 20)b
21)b 22)a 23)b 24)d 25)b 26)c 27)d 28)c 29)d 30)a 31)d 32)a 33)d 34)a 35)d 36)d 37)a 38)b 39)b
40)a 41)a 42)b 43)c 44)d 45)c 46)b 47)d 48)e 49)b 50)b 51)c 52)b 53)b
Exercícios de Log Enem
01. (Enem 11) A Escala de Magnitude de Momento (abreviada como MMS e denotada como
),
introduzida em 1979 por Thomas Haks e Hiroo Kanamori, substituiu a Escala de Richter para medir a
magnitude dos terremotos em termos de energia liberada. Menos conhecida pelo público, a MMS é, no
entanto, a escala usada para estimar as magnitudes de todos os grandes terremotos da atualidade. Assim
como a escala Richter, a MMS é uma escala logarítmica.
e
se relacionam pela fórmula:
= -10,7 +
( )
Onde
é o momento sísmico (usualmente estimado a partir dos registros de movimento da superfície,
através dos sismogramas), cuja unidade é o dina·cm. O terremoto de Kobe, acontecido no dia 17 de janeiro
de 1995, foi um dos terremotos que causaram maior impacto no Japão e na comunidade científica
internacional. Teve magnitude
= 7,3.
Mostrando que é possível determinar a medida por meio de conhecimentos matemáticos, qual foi o
momento sísmico
do terremoto de Kobe (em dina.cm)? (e)
a)
b)
c)
d)
e)
02. (Enem 13) Em setembro de 1987, Goiânia foi palco do maior acidente radioativo ocorrido no Brasil,
quando uma amostra de césio-137, removida de um aparelho de radioterapia abandonado, foi manipulada
inadvertidamente por parte da população. A meia-vida de um material radioativo é o tempo necessário
para que a massa desse material se reduza a metade. A meia-vida do césio-137 é 30 anos e a quantidade
restante de massa de um material radioativo, após t anos, é calculada pela expressão M(t) = A . (2,7)kt, onde
A é a massa inicial e k uma constante negativa.
Considere 0,3 como aproximação para log102.
CURSOS MIGUEL - Centro Preparatório Para Concursos
11
WWW.CURSOSMIGUEL.COM.BR
Matemática – Caderno 5
Qual o tempo necessário, em anos, para que uma quantidade de massa do césio-137 se reduza a 10% da
quantidade inicial? (e)
a) 27
b) 36
c) 50
d) 54
e) 100
/2013
03. (Enem 15) Um engenheiro projetou um automóvel cujos vidros das portas dianteiras foram desenhados
de forma que suas bordas superiores fossem representadas pela curva de equação y = log (x), conforme a
figura. (e)
A forma do vidro foi concebida de modo que o eixo x sempre divida ao meio a altura h do vidro e a base do
vidro seja paralela ao eixo x. obedecendo a essas condições, o engenheiro determinou uma expressão que
fornece a altura h do vidro em função da medida n de sua base, em metros.
A expressão algébrica que determina a altura do vidro é (e)
CURSOS MIGUEL - Centro Preparatório Para Concursos
12
WWW.CURSOSMIGUEL.COM.BR
CURSOS MIGUEL - Centro Preparatório Para Concursos
Matemática – Caderno 5
13
WWW.CURSOSMIGUEL.COM.BR
Matemática – Caderno 5
Inequação Logarítmica:
Chama-se inequação logarítmica aquela que apresenta a incógnita no logaritmando ou na base de um
logaritmo.
Exemplos
a) log 2 (3x – 1) > 3
b) log 1/2 (x – 1) + log 1/2 (x +5)  -4 c) log x 9 > 1
As inequações logarítmicas são resolvidas por meio das seguintes propriedades:
P1. Sendo (x1, x2, b)  IR* + , log b x2 > log b x2 ↔ x2 > x1, com b > 1.
P2. Sendo (x1, x2, a)  IR* + , log b x2 > log b x2 ↔ x2 < x1, com 0< b < 1.
Determinação do Domínio de Funções
Inequações
Inequações são sentenças matemáticas do tipo:
f ( x)  g ( x);
f ( x)  g ( x);
f ( x)  g ( x);
f ( x)  g ( x);
Resolver uma inequacão significa determinar os valores de x que satisfazem tal desigualdade.
Para facilitar sua aprendizagem, vamos separar as inequações em dois tipos diferentes.
1º Tipo:
Inequações do 1º Grau e do 2º Grau
1) Resolva a seguinte inequacão: - 2x < x – 90
2) Resolva a seguinte inequacão: x2 - 5x + 6  0
3) Resolva a seguinte inequacão: - 2x2 + 3x + 2 < 0
2º Tipo:
Inequações Produto ou Quociente
4) Resolva a seguinte inequacão: (x – 2) . (x2 – 4x + 3)  0
5) Resolva a seguinte inequacão:
x²  x
0
x ²  3x  2
CURSOS MIGUEL - Centro Preparatório Para Concursos
14
WWW.CURSOSMIGUEL.COM.BR
MATEMÁTICA MÓDULO II
Domínio
Determinar o domínio de uma função f(x) significa achar os valores de x para os quais a função
existe.
É importante lembrar da aritmética dos números reais que um denominador nunca poderá se
anular e que não existe raiz com índice par de um número negativo.
Em resumo
a
b 0
b
par
coisa  coisa  0
log b a  a  0, b  0 e b  1
par
fração  fração  0
1) Determine o domínio da seguinte Função: f(x) =
x²  5x  6
10  x
2) Determine o domínio da seguinte Função: f(x) =
x 1
x²  2 x
3) Determine o domínio da seguinte Função: f(x) =
100  x
x ²  11x  28
Testes
1 – o intervalo que corresponde à solução da inequação x² - x -2 >0 é:
a) (-1; 2)
b) (-2; 1)
c) (-  ; -1)  (2; ) d)  ;2  1; 
2 – As soluções de x2 – 2x < 0 são valores de x pertencentes ao conjunto:
a) (0,2)
b) (-  , 0)
c) (2,  )
d) (-  ,0)  (2, )
e) (-2; 2)
e) (0, )
3 – (UFRGS) As soluções reais da desigualdade x2 +1 > 2x são os números x, tais que.
a) x  0
b) x  1
c) x > 1
d) x  1
4 - A menor solução inteira de x2 – 2x – 35 < 0
a) -5
b) -4
c) -3
d) -2
e) x < 1
e) -1
5 – O Conjunto solução de x2 – 4x + 4  0 é :
a) x   / x 2  0 
b) x   /  2  x  2 
c) { 2 }
d) { 4 }
e) {x   / x  2 

CURSOS MIGUEL - Centro Preparatório Para Concursos
15
WWW.CURSOSMIGUEL.COM.BR
MATEMÁTICA MÓDULO II
6 – O conjunto solução da inequacão
(x2 – 7x + 12 ) . (x2 – 16) < 0 é:
a) (-4,3)
b) (- ,3)  (4, )
c) 3,  
d) 3,4
e) 4,  
7. Os valores de x que satisfazem a inequação
x 2  4x  4
 0 são:
x 2  7 x 12
a) 2  x  3
b) 2  x  4
c) 3  x  4
d) x  3
e) x < 3 OU x > 4
8 – (PEIES) A solução da inequação
( 3 – x ) ( x - 32 ) < 0 é o conjunto
a)  32 ,3 
b)
32 ,3 
c) (, 32   3,  )
d) ( - , 32   3, )
e) ( 32 ,3]
9 – O conjunto solução da inequacão (x + 3 ) ( x – 2 )  0
a) {x   /
b) {x   /
c) {x   /
d) {x   /
e) {x   /
x3 
2  x 3 
x  2 ou x  3
 3 x  2 
 2 x 3 

10 – O número de soluções inteiras da inequação
a)6
b)5
c)4
d)7
e)3
( x 2  2 x7) ( x 2  7 x 6) 0 é :
x 2  5x  6
 0 são:
x2
c) x < 2 ou x > 3 d) x  2 e) x < 3 e x  2
11(PUC) Os valores de x que verificam
a) x < 3
b) 2 < x < 3
CURSOS MIGUEL - Centro Preparatório Para Concursos
16
WWW.CURSOSMIGUEL.COM.BR
12 – (UFSM) Seja a inequação
MATEMÁTICA MÓDULO II
5  x2
 0 , com x  2 . Sua solução é :
2 x
a) ] - , 5 ]  ] 2, 5 ]
b) ] -2,-5]  ]2,5 ]
c) ] 2,+  [
d) [ -5,5 ]
e) 
9 x2
13 – O conjunto solução da inequação
0 é :
x
a) x  3
b)  3  x  3 e x  0
c) 
d) os reais negativos
e) x  3 ou 0  x  3
14 - O conjunto de todos os números reais que satisfazem a inequação
a) { 0 }
b) {0, 12 }
2
 1é :
x 1
c) x  ,1  x  1
d) {x  , x  0}
e) {x  , x  1 ou x  3}
15 – (PEIES) – Dadas as funções reais expressas por: f(x) = 2x -4 e g(x) = -x + 4, a intersecção
dos intervalos tais que f(x) > 0 e g(x)  0 é:
a)  * ={x   / x  0
b) ]2,4]
c)  * ={x   / x  0
d) [2,4[
e) ]2,4[
16 – O domínio da função f(x)= x 2  9 é dado por :
a)  x   / x  3 ou x  3
b) x   /  3  x  3
c) x   / x  3
d) x   / x  3
e) 

17 – (FURG) O domínio da função f(x)=
x 2  3x 10
é:
1 x
a) (1,2]
b) (-  , 5]
c) (-  , -5)  (1,2)
d) (-  , -5)
e) (-  , -5]  (1,2]
CURSOS MIGUEL - Centro Preparatório Para Concursos
17
WWW.CURSOSMIGUEL.COM.BR
18 - Dada a função f(x)=
a) x   / x  0 ou x  1
b) x   / x  0 ou x  1
c)  x   / x  0 ou x  1
d) { x € IR/ 0≤ x ≤ 1
e) x   / 0  x  1
19 – (URI) Se f(x)=
MATEMÁTICA MÓDULO II
x
o seu domínio é:
x 1

x  1. x  3, o domínio de f(x) será:
a) x   / x  1
b) x   /  3  x  1
c) x   / x  3
d) x   / x  3 e x  1
e) x   / x  3 e x  1
20 – (PEIES-95)O domínio da função f(x)=
1
2  x  x2
é
a) ]-2, 1[
b) ]0,  [
c) [-2, 1[
d) ]-  , -2[  [1,  [
e) ]- , -2[  ]1,  [
21 – (PEIES-96)O domínio da função f(x)=
a) (-1,2)
b) [-1,2]
x2
é
1 x
c) (-  , 1]  [2,  ] d) (-  , -1]  (2,  )
22 – (PEIES-97)O domínio da função f(x)=
1
( x  1).(2 x  3)
e) (-  , -1)  [2,  )
é
a) ]- 32 ,1[
b) (- , 32 [  ]1,  )
c) (-  ,- 32 [  [1,  )
d) [- 32 ,1]
e) (-  , - 32 ]  [1,  )
 x 2  4x  3 
 é o conjunto de números reais dado por
 x2 
23 – (PEIES) O domínio da função f(x)=log 10 
a) ]- , [
b) ]-3, -2[  [-1,3]
c) ]-3, -2[  ]-1,+  [
d) ]-3, -1]  [3,+  [
e) ]-2,+  [
CURSOS MIGUEL - Centro Preparatório Para Concursos
18
WWW.CURSOSMIGUEL.COM.BR
MATEMÁTICA MÓDULO II
24–(PEIES) O domino da função real f(x)=
a) ]-  ,-3[  ]-3, 0]  ] 3,  [
b) ]-  ,-3[  ]3,  [
c) ]3,  [
d) x   : x 2  9  0
e) ]-  ,  [

x
1
é o conjunto:
 2
x3 x 9

25 – (UFSM) Seja f:A   tal que
 x 1 
 Então o domínio da função é
 x  2
2
f(x)= x  3x  2  log
a) (-  , -2)  [2,  )
b) (-  ,-2)  (2,  )
c) (-2, 2]
d) (-  , -2]  (2,  )
e) (-  , -2]  [2,  )
26 – (PEIES) O domínio da função f(x)=
a) ]-  , -1[  [1,2[  ]3,+  [
b) ]-  ,+  [
c) ]-  ,1]  [2,+  )
d) x   / x  1 ou x  1
e) x   / x  1 ou x  3
x y =
27 – (UFSM) Seja f: A  
x 1
 log 10 ( x 2  5x  6) em  ,é o subconjunto
x 1
1
 2  3x  2 x 2 onde A   .
2x  1
Então , o domínio da função f é:


1  1 
  ,1
2   2 
1

e)   ,   2, 
2

 1
 2
 1 
d)   ,2 
 2 
a)    
b)   4, 
 1 
, 2
 2 
c)   
28. (EsSA) A soma dos dois primeiros números inteiros do domínio da função definida por
g(x) =
1
9
2 x 1
 32 x 4
a) 3
é:
b) 1
c) -1
d) 5
e) 7
29. (EsPCEx) Assinale a alternativa que representa o conjunto de todos os números reais para os quais
está definida a função
f (x) =
√
√
.
a) ıR – [-2, 2]
b)(c)(d)(e)(-
CURSOS MIGUEL - Centro Preparatório Para Concursos
19
WWW.CURSOSMIGUEL.COM.BR
MATEMÁTICA MÓDULO II
30. (EsPCEx 15) Considere as funções reais f e g, tais que f(x) = √ +4 e f(g(x)) = x2 – 5, onde g(x) é não
negativa para todo x real. Assinale a alternativa cujo conjunto contém todos os possíveis valores de x,
que satisfazem os dados do enunciado.
a) IR - ] -3, 3[
b) IR - ] -√ , √ [
c) ] -√ , √ [
d) ] -3, 3[
e) IR - ] -∞, 3[
GAB: 01)C
11)E
21)E
02)A
12)A
22)B
03)D
13)E
23)C
04)B
14)E
24)A
05)C
15)B
25)A
06)A
16)A
07)E
17)E
26)A
27)D
08)C
18)A
09)D
19)E
10)A
20)A
28)D 29)C 30)A
Logaritmo natural
Quando nos deparamos com logaritmos em grande parte estudamos os logaritmos decimais que são
logaritmos cuja base é representada pelo número 10 - que normalmente oculta-se o mesmo em sua
representação. Os logaritmos Naturais são logaritmos representados pela base “e” que é um número
irracional denominado de constante ou número de Euler equivalente a (e=2,71828..).
Matematicamente representamos o logaritmo natural por;
Ln(x) = logex
Portanto, algumas consequências de sua definição podem ser representadas:



Ln 1 = 0
Ln e = 1
Ln (en) = n
Também podemos listar aqui suas propriedades operacionais importantes.
1. Logaritmo natural de um produto

ln (x · y) = ln x + ln y
2. Logaritmo natural de um quociente

ln (x/y) = ln x - ln y
3. Logaritmo natural de uma potência

ln (xn) = n . ln x
Muitos exercícios referentes a logaritmos naturais podem ser resolvidos a partir de técnicas utilizadas
para facilitar a resolução dos mesmos. Vejamos;
Iremos transformar a base “e” para a base decimal (10)
CURSOS MIGUEL - Centro Preparatório Para Concursos
20
WWW.CURSOSMIGUEL.COM.BR
MATEMÁTICA MÓDULO II
Demonstração
Ln x = logex
Fazendo a mudança de base para a base decimal
Logex= Log10x / log10e
Resolvendo
Logex =Log10x /0,434
“Desmembrando”
Logex= 1 /0,434 . Log10x
Logex = 2,31 Log10x ( Obs: Valor aproximado, uma vez que o valor de” log10e”foi truncado)
Agora vejamos algumas aplicações em exercícios sobre o conceitos descritos acima.
Exemplo 1) Se Log 8=0,90, determine o valor de Ln(8).
Resolução
Ln8= Loge8 = 2,31 log108 = 2,31 x 0,90= 2,1.
Exemplo 2) Se Ln 3=1,1 e Ln 6=1,8. Determinar o valor de Ln 18.
Resolução
Aplicando a regra do produto
Ln 18= Ln(3 . 6)= Ln 3+ Ln6 = 2,9
Nota: Não devemos confundir os termos referentes a logaritmo natural e logaritmo neperiano, muita
das vezes ambos são tratados como sinônimos, mas na verdade o logaritmo neperiano refere-se a um
logaritmo na qual sua base é denotada por “a”, onde se segue;
107 . log a (x/107)
a= (1-10-7)10^7 = limn->∞(1-1/n)n= 1/e
107 .log1/e (x/107)
Logo, percebe-se que o logaritmo neperiano refere-se a base ”1/e”.
CURSOS MIGUEL - Centro Preparatório Para Concursos
21
WWW.CURSOSMIGUEL.COM.BR
MATEMÁTICA MÓDULO II
Exercícios
01. (Enem 2009) Suponha o modelo exponencial y = 363 e0,03x, em que x = 0 corresponde ao ano 2000,
x = 1 corresponde ao ano 2001, e assim sucessivamente, e que y é a população em milhões de
habitantes no ano x, seja usado para estimar essa população com 60 anos ou m ais de idade nos países
em desenvolvimento entre 2010 e 2050. Desse modo, considerando
e0,3 = 1,35, estima-se que a população com 60 anos ou mais estará, em 2030, entre: (e)
a) 490 e 510 milhões
b) 550 e 620 milhões
c) 780 e 800 milhões
d) 810 e 860 milhões
e) 870 e 910 milhões
02. O número de bactérias N em um meio de cultura que cresce
exponencialmente pode ser determinado pela equação
ekt em que
é a quantidade inicial,
isto é, N= N (0), e k é a constante de proporcionalidade. Se inicialmente havia 5000 bactérias na
cultura e 8000 bactérias 10 minutos depois, quanto tempo será necessário para que o número de
bactérias se torne duas vezes maior que o inicial? (c)
(Dados: In 2 = 0,69 In 5 = 1,61)
a) 11 minutos e 25 segundos.
b) 11 minutos e 15 segundos.
c) 15 minutos.
d) 25 minutos.
e) 25 minutos e 30 segundos.
03.(EsPCEx) Fazendo x=ln5 temos que y = ex – e-x = , a ϵ Z e b ϵ Z*, a e b primos entre si. Logo a + b é
igual a: (b)
a) 28
b) 29
c) 40
d) 51
e) 52
04. Em quantos anos 500g de uma substância radioativa, que se desintegra a uma taxa de 3% ao ano,
se reduzirão a 100g? Use Ln 5 = 1,609 e Q = Qo.e-rt, em que Q é a massa da substância, r a taxa e t é
o tempo em anos. R: 53,63anos
CURSOS MIGUEL - Centro Preparatório Para Concursos
22