FIS-14 — Lista-10 — Outubro/2012

FIS-14 — Lista-10 — Outubro/2012
———————————————————————————
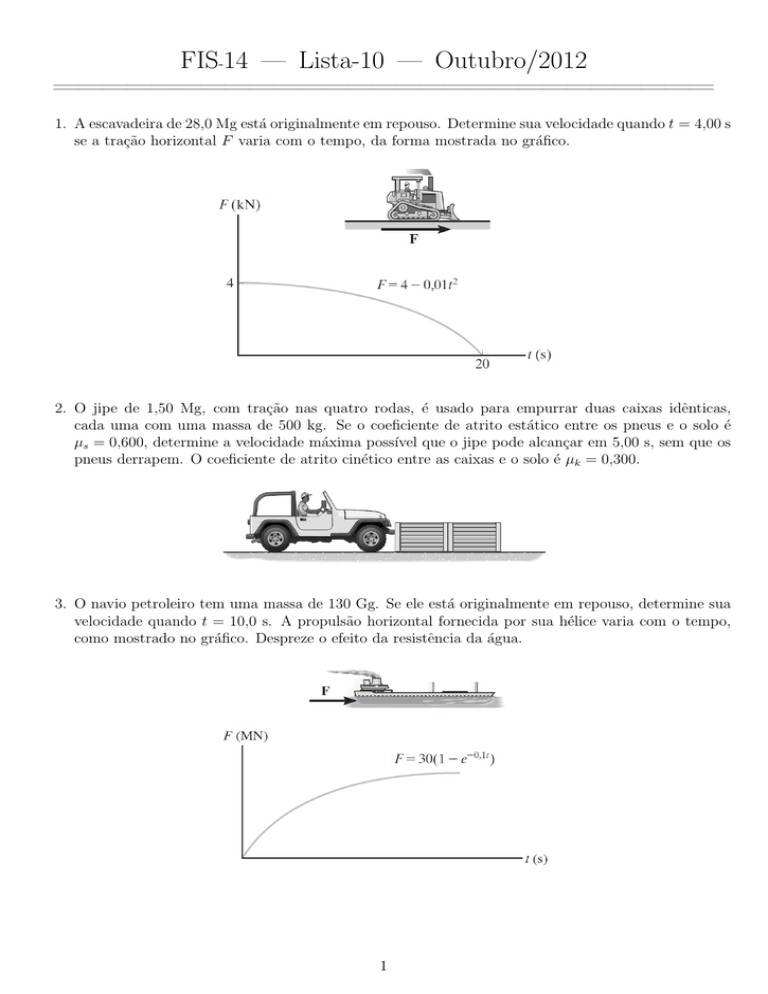
1. A escavadeira de 28,0 Mg está originalmente em repouso. Determine sua velocidade quando t = 4,00 s
se a tração horizontal F varia com o tempo, da forma mostrada no gráfico.
2. O jipe de 1,50 Mg, com tração nas quatro rodas, é usado para empurrar duas caixas idênticas,
cada uma com uma massa de 500 kg. Se o coeficiente de atrito estático entre os pneus e o solo é
µs = 0,600, determine a velocidade máxima possı́vel que o jipe pode alcançar em 5,00 s, sem que os
pneus derrapem. O coeficiente de atrito cinético entre as caixas e o solo é µk = 0,300.
3. O navio petroleiro tem uma massa de 130 Gg. Se ele está originalmente em repouso, determine sua
velocidade quando t = 10,0 s. A propulsão horizontal fornecida por sua hélice varia com o tempo,
como mostrado no gráfico. Despreze o efeito da resistência da água.
1
4. A caixa de 100 kg é içada pelo motor M . O motor exerce no cabo uma força T = (200t1/2 + 150) N,
onde t está em segundos. Se a caixa parte do repouso no solo, determine a velocidade da caixa
quando t = 5,00 s.
5. A força atuando sobre um projétil que tem massa m, enquanto este passa horizontalmente pelo cano
do canhão é F = Csen(πt/t0 ). Determine a velocidade do projétil quando t = t0 . Se o projétil alcança
o final do cano nesse instante, determine o comprimento s.
6. Uma partı́cula de 0,5 kg sofre a ação da força F~ = {2,00t2 i − (3,00t + 3,00)j + (10,0 − t2 )k} N, onde
t está em segundos. Se a partı́cula tem uma velocidade inicial de v~0 = {5,00i + 10,0j + 20,0k} m/s,
determine a intensidade da velocidade da partı́cula quando t = 3,00 s.
7. A bola de beisebol de 0,150 kg tem uma velocidade de v = 30,0 m/s, imediatamente antes de ser
atingida pelo taco. Após isso, ela desloca-se ao longo da trajetória mostrada, antes que o apanhador
a pegue. Determine a intensidade da força impulsiva média transmitida à bola, se esta esteve em
contato com o taco durante 0,750 ms.
2
8. O guincho na traseira do jipe A é acionado e puxa o cabo de reboque a 2,00 m/s, medidos relativamente ao jipe. Se tanto o carro B, de 1,25 Mg, quanto o jipe A, de 2,50 Mg, estão livres para se
moverem, determine suas velocidades no instante em que se encontram. Se o cabo tem 5,00 m de
comprimento, quanto tempo isso levará?
9. Se o homem de 75,0 kg dispara a bala de 0,100 kg, a uma velocidade de saı́da horizontal de 900 m/s,
medida relativamente ao carrinho de 300 kg, determine a velocidade do carrinho logo após o disparo.
Qual é a velocidade do carrinho quando a bala penetra no alvo? Durante o disparo, o homem
permanece na mesma posição sobre o carrinho. Despreze a resistência ao rolamento do carrinho.
10. O carrinho B de 10,0 kg está apoiado em roletes de dimensão desprezı́vel. Se uma maleta A de
5,00 kg é lançada horizontalmente sobre o carrinho a 3,00 m/s quando ele está em repouso, determine
o perı́odo de tempo que A desliza relativamente a B e a velocidade final de A e B. O coeficiente de
atrito cinético entre A e B é µk = 0,400.
11. Uma bola de 1,00 kg está viajando horizontalmente a 20,0 m/s quando atinge um bloco B de 10,0 kg
que está em repouso. Se o coeficiente de restituição entre A e B é e = 0,600, e o coeficiente de atrito
cinético entre o plano e o bloco é µk = 0,400, determine a distância que o bloco B desliza sobre o
plano antes de parar.
3
12. A bola de 2,00 kg é lançada até o bloco suspenso de 20,0 kg a uma velocidade de 4,00 m/s. Se o
tempo de impacto entre a bola e o bloco é 5,00 ms, determine a força normal média exercida sobre
o bloco durante esse tempo. Considere e = 0,800.
13. A estaca P tem massa de 800 kg e está sendo enterrada na areia solta por um martelo C, de 300 kg,
que é deixado cair a uma distância de 0,500 m do topo da estaca. Determine a distância que a estaca
penetra na areia após um golpe, se a areia oferece uma resistência de atrito de 18,0 kN contra a
estaca. O coeficiente de restituição entre martelo e estaca é e = 0,100. Despreze os impulsos devidos
aos pesos da estaca e do martelo e o impulso devido à areia durante o impacto.
14. Uma bola tem massa m e é deixada cair sobre uma superfı́cie a partir de uma altura h. Se o
coeficiente de restituição entre a bola e a superfı́cie é e, determine o tempo necessário para a bola
parar de quicar.
15. Para testar as propriedades de fabricação de bolas de aço de 1,00 kg, cada bola é liberada do repouso
como mostrado e atinge a superfı́cie lisa inclinada de 45o . Se o coeficiente de restituição é e = 0,800,
determine a distância S até onde a bola atinge o plano horizontal em A. Em que velocidade a bola
atinge o ponto A?
4
16. Cada uma das três bolas tem uma massa m. Se A é liberada do repouso em θ, determine o ângulo
φ para o qual C eleva-se após a colisão. O coeficiente de restituição entre cada bola é e.
17. A garota lança a bola de 0,500 kg na direção da parede, a uma velocidade inicial de vA = 10,0 m/s.
Determine: (a) a velocidade com que a bola atinge a parede em B; (b) a velocidade com a qual ela
quica na parede se o coeficiente de restituição for e = 0,500; (c) a distância s, da parede até onde
ela atinge o solo em C.
18. Dois carros A e B tem massa de 2000 kg e colidem no pavimento escorregadio de um cruzamento. A
direção do movimento de cada carro após a colisão é medida pelos rastros deixados, como mostrado.
Se o motorista do carro A afirma que vinha a 15,00 m/s (54,00 km/h) imediatamente antes da
colisão e que, após a mesma, acionou os freios de modo que o carro derrapou 3,000 m antes de
parar, determine a velocidade aproximada do carro B imediatamente antes da colisão. Suponha que
o coeficiente de atrito cinético entre as rodas do carro e o pavimento é µk = 0,1500. Nota: a linha
de impacto não foi definida; no entanto, essa informação não é necessária para a solução.
5
19. Dois discos A e B têm massa de 1,00 kg e 2,50 kg, respectivamente. Se eles deslizam sobre um plano
horizontal liso com as velocidades mostradas, determine suas velocidades logo após o impacto. O
coeficiente de restituição entre os discos é e = 0,600.
20. A bola A atinge a bola B com uma velocidade inicial (vA )1 como mostrado. Se as duas bolas têm
a mesma massa e a colisão é perfeitamente elástica, determine o ângulo θ após a colisão. A bola B
está originalmente em repouso. Despreze a dimensão de cada bola.
21. Se uma barra de massa desprezı́vel está sujeita a um momento de binário M = (30t2 ) N · m, e o
motor do carro fornece uma força de tração F = (15t) N às rodas, onde t está em segundos, determine
a velocidade do carro no instante t = 5,00 s. O carro parte do repouso. A massa total do carro e do
motorista é 150 kg. Despreze a dimensão do carro.
6
22. O bloco de 5,00 kg está originalmente em repouso sobre a superfı́cie lisa. Sobre ele aje uma força
radial de 10,0 N e uma força horizontal de 35,0 N, sempre dirigida a 30o da tangente à trajetória,
como mostrado. Determine o tempo necessário para romper a corda, que requer uma tração de
T = 150 N. Qual é a velocidade do bloco quando isso ocorre? Despreze para o cálculo a dimensão
do bloco.
23. Uma atração de parque de diversões consiste de um carro que está fixo ao cabo OA. O carro gira
em uma trajetória circular horizontal e atinge velocidade v1 = 1,20 m/s, quando r = 3,60 m. O
cabo é então recolhido a uma taxa constante de 0,150 m/s. Determine a velocidade do carro em 3,00
segundos.
24. Um satélite de massa 700 kg é lançado em uma trajetória de voo livre em torno da Terra a uma
velocidade inicial vA = 10,0 km/s, quando a distância do centro da Terra é rA = 15,0 Mm. Se o
ângulo de lançamento nessa posição é φA = 70o , determine a velocidade vB do satélite e sua distância
mais próxima, rB , do centro da Terra. A Terra tem uma massa Me = 5,976(102 4) kg. Dica: sob
estas condições, o satélite está sujeito apenas à força gravitacional da Terra, F = GMe ms /r2 . Para
obter parte da solução, use a conservação da energia.
7
25. A bola de 2,00 kg gira em torno de uma trajetória circular de 0,500 m de diâmetro com velocidade
constante. Se o comprimento da corda é encurtado de l = 1,00 m até l0 = 0,500 m, puxando-se a
corda através do tubo, determine o novo diâmetro da trajetória d0 . Além disso, qual é a tração na
corda em cada caso?
26. Um ginasta de massa 80,0 kg segura duas argolas para baixo com seus braços na posição mostrada
quando ele oscila para baixo. Seu centro de massa está localizado no ponto G1 . Quando ele está
na posição mais baixa de sua oscilação, sua velocidade é (vG )1 = 5,00 m/s. Nessa posição, ele de
repente deixa que os braços subam, mudando seu centro de massa para a posição G2 . Determine
sua nova velocidade na oscilação para cima e o ângulo θ para o qual ele oscila antes de entrar
momentaneamente em repouso. Considere o corpo dele como uma partı́cula.
27. Ao pequeno rolamento de massa m é dada uma velocidade v0 em A, paralela à borda horizontal de
uma tigela lisa. Determine a intensidade da velocidade v da bola, quando esta houver caı́do uma
distância vertical h para atingir o ponto B. O ângulo θ é medido a partir de v até a horizontal no
ponto B.
8
28. Um jato jumbo comercial de quatro motores está em cruzeiro a uma velocidade constante de
800 km/h, em voo nivelado com os quatro motores em operação. Cada um dos motores é capaz
de descarregar gases da combustão a uma velocidade de 775 m/s em relação ao avião. Se, durante
um teste dois dos motores, um de cada lado do avião, são desligados, determine a nova velocidade de
cruzeiro do jato. Suponha que a resistência do ar (arrasto) é proporcional ao quadrado da velocidade,
isto é, FD = cv 2 , onde c é uma constante a ser determinada. Despreze a perda de massa devido ao
consumo de combustı́vel.
29. Em operação, o ventilador de jato de ar descarrega o ar a uma velocidade de vB = 20,0 m/s para
dentro de um bocal tendo um diâmetro de 0,500 m. Se o ar tem uma densidade de 1,22 kg/m3 ,
determine as componentes da reação horizontal e vertical em C e a reação vertical em cada uma das
duas rodas, D, quando o ventilador está em operação. O ventilador e o motor têm massa de 20,0 kg
e centro de massa em G. Despreze o preço da estrutura. Devido à simetria, as duas rodas suportam
cargas iguais. Suponha que o ar que entra no ventilador em A está essencialmente em repouso.
30. Uma lancha é propelida pelo motor a jato mostrado na figura. A água do mar é puxada pela bomba,
a uma vazão de 0,540 m3 /s, através de uma entrada A, de 150 mm de diâmetro. Uma hélice acelera
a vazão de água e a força para fora horizontalmente, através de uma saı́da de 100 mm de diâmetro,
B. Determine as componentes horizontal e vertical do empuxo exercidas sobre a lancha. O peso
especı́fico da água do mar é γsw = 10,0 kN/m3 .
9
31. O escoadouro é usado para desviar o curso da água, Q = 0,600 m3 /s. Se a água tem uma área
de seção transversal de 5,00 · 10−2 m2 , determine as componentes da força , no pino D e no rolete
C, necessárias para o equilı́brio. Despreze o peso do escoadouro e o peso da água dentro dele.
ρw = 1,00 Mg/m3 .
32. O trator com o tanque vazio tem massa total de 4,00 Mg. O tanque fica cheio com 2,00 Mg de água.
A água é descarregada a uma taxa constante de 50,0 kg/s, a uma velocidade constante de 5,00 m/s,
medida em relação ao trator. Se o trator parte do repouso, e as rodas traseiras fornecem uma força
de tração resultante de 250 N, determine a velocidade e a aceleração do trator no instante em que o
tanque esvazia-se.
33. O carrinho tem massa M e está cheio de água que tem massa m0 . Se uma bomba ejeta água por um
bocal que tem uma área de seção transversal A, a uma taxa constante de v0 em relação ao carrinho,
determine a velocidade do carrinho como uma função de tempo. Qual é a velocidade máxima do
carrinho, supondo-se que toda a água pode ser bombeada para fora? A resistência ao atrito do
movimento à frente é F . A densidade da água é ρ.
10
34. A corrente tem um comprimento total L < d e uma massa por unidade de comprimento m0 . Se uma
porção h da corrente é suspensa sobre a mesa e liberada, determine a velocidade de sua extremidade
A como uma função de sua posição y. Despreze o atrito.
35. Um avião comercial a jato tem massa de 150 Mg e está viajando a uma velocidade constante de
850 km/h em linha reta (θ = 0o ). Se cada um dos dois motores absorve ar a uma taxa de 1,00·103 kg/s
e o ejeta a uma velocidade de 900 m/s em relação à aeronave, determine o ângulo máximo de
inclinação θ, no qual a aeronave pode voar com uma velocidade constante de 750 km/h. Suponha
que a resistência do ar (arrasto) é proporcional ao quadrado da velocidade, isto é, FD = cv 2 , onde c
é uma constante a ser determinada. Os motores estão operando com a mesma potência em ambos
os casos. Despreze a quantidade de combustı́vel consumida.
36. Determine a intensidade da força F como uma função do tempo, que deve ser aplicada à extremidade
da corda em A para levantar o gancho H com uma velocidade constante v = 0,400 m/s. Inicialmente,
a corrente está em repouso sobre o solo. Despreze a massa da corda e do gancho. A corrente tem
massa de 2,00 kg/m.
11
37. A escavadeira carrega inicialmente 10,0 m3 de areia com uma densidade de 1,52 · 103 kg/m3 . A areia
é descarregada horizontalmente através de uma portinhola P , de 2,50 m2 , a uma taxa de 900 kg/s,
medida em relação à portinhola. Se a escavadeira mantém uma força de tração resultante constante
F = 4,00 kN em suas rodas dianteiras para fornecer movimento à frente, determine sua aceleração
quando metade da areia for despejada. Quando vazia, a escavadeira tem massa de 30,0 Mg. Despreze
qualquer resistência ao movimento à frente e a massa das rodas. As rodas traseiras estão livres para
rodar.
38. O foguete tem uma massa inicial m0 , incluindo o combustı́vel. Por razões práticas de conveniência da
tripulação, é necessário que ele mantenha uma aceleracão ascendente constante a0 . Se o combustı́vel
é expelido do foguete a uma velocidade relativa ve/r , determine a taxa na qual o combustı́vel deve
ser consumido para manter o movimento. Despreze a resistência do ar e suponha que a aceleração
gravitacional é constante.
39. Se a corrente é abaixada a uma velocidade constante, determine a reação normal exercida sobre o
solo como uma função do tempo. A corrente tem massa de 10,0 kg/m e um comprimento total de
6,00 m.
12
Respostas
1. v = 0,564 m/s
2. v = 11,8 m/s
3. v = 0,849 m/s
4. v = 2,34 m/s
5. v2 = 2Ct0 /πm, s = Ct02 /πm
6. v2 = 82,2 m/s
7. F = 12,7kN
8. vA = 0,667 m/s, vB = 1,33 m/s, t = 2,50 s
9. (vC )2 = −0,240 m/s, v3 = 0
10. v = 1,00 m/s, t = 0,510 s, s = 0,255 m
11. d = 1,08 m
12. F = 2,62 kN
13. d = 34,8 mm
p
14. ttot = 2h/g(1 + e)/(1 − e)
15. vA = 5,12 m/s, s = 0,571 m
16. φ = arccos[1 − (1 + e)4 (1 − cos θ)/16]
17. (vB )1 = 8,81 m/s, (vB )2 = 4,62 m/s, θ = 10,5o , φ = 20,3o , s = 3,96 m
18. (vB )1 = 9,833 m/s
19. vA0 = 3,30 m/s, vB = 1,76 m/s, θA = 18,8o , θB = 58,3o
20. θ = 90o
21. v = 3,33 m/s
22. v = 5,42 m/s, t = 0,894 s
23. v2 = 1,38 m/s
24. vθ = 10,2 km/s, rθ = 13,8 Mm
25. T1 = 20,3 N, T2 = 21,6 N, d0 = 0,414 m
26. v2 = 4,31 m/s, θ = 33,2o
p
27. v = v02 + 2gh
28. vp = 594 km/h
29. Cx = 95,8 N, Cy = 118 N, Dy = 38,9 N
30. Fx = 25,9 kN, Fy = 11,9 kN
13
31. Cx = 4,97 kN, Dx = 2,23 kN, Dy = 7,20 kN
32. a = 0,125 m/s2 , v = 4,05 m/s
33. v = (ρAv02 − F )/(ρAv0 ) ln[(M + m0 )/(M + m0 − ρAv0 t)], vmax = (ρAv02 − F )/(ρAv0 ) ln[(M + m0 )/M ]
p
34. 2g(y 3 − h3 )/3y 2
35. θ = 13,7o
36. F = (7,85t + 0,320) N
37. F = 3,55 kN
38. dm/dt = m0 (a0 + g)e[(a0 +g)ve/r ]t /ve/r
39. R = (11,8t + 14,4) N
14