Física - Mecânica Clássica

www.fisicaexe.com.br
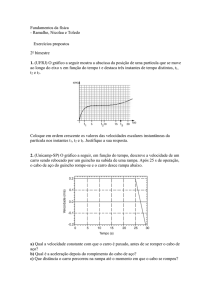
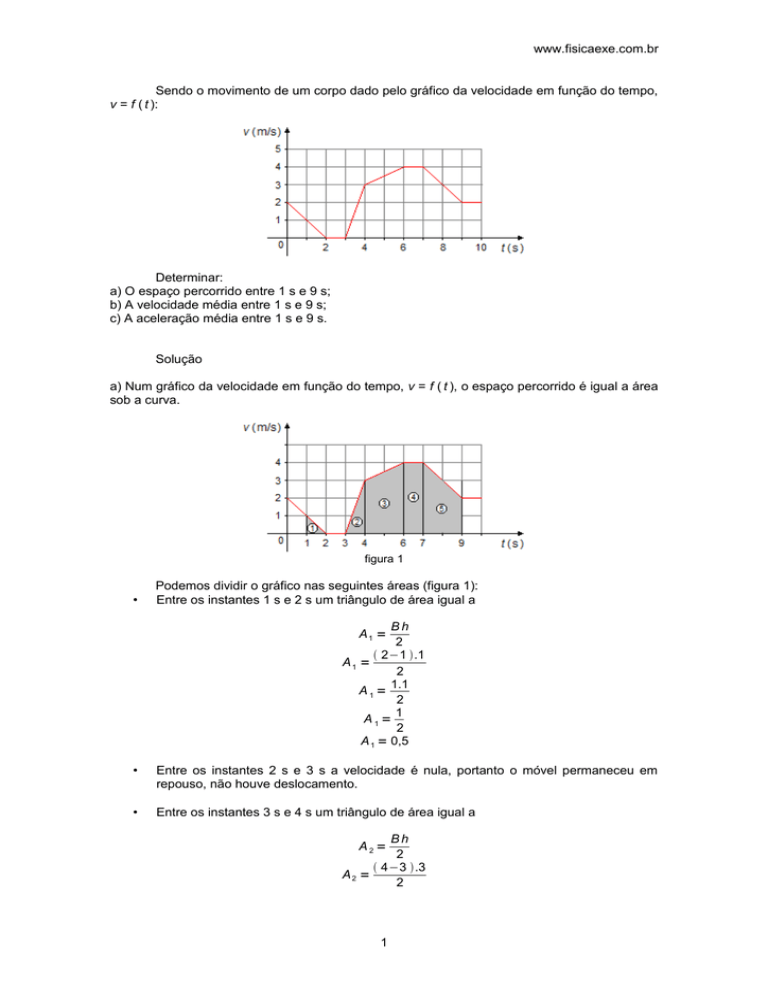
Sendo o movimento de um corpo dado pelo gráfico da velocidade em função do tempo,
v = f ( t ):
Determinar:
a) O espaço percorrido entre 1 s e 9 s;
b) A velocidade média entre 1 s e 9 s;
c) A aceleração média entre 1 s e 9 s.
Solução
a) Num gráfico da velocidade em função do tempo, v = f ( t ), o espaço percorrido é igual a área
sob a curva.
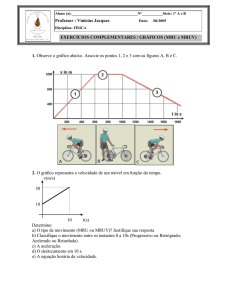
figura 1
•
Podemos dividir o gráfico nas seguintes áreas (figura 1):
Entre os instantes 1 s e 2 s um triângulo de área igual a
Bh
2
 2−1 .1
A1 =
2
1.1
A1=
2
1
A1=
2
A 1 = 0,5
A1 =
•
Entre os instantes 2 s e 3 s a velocidade é nula, portanto o móvel permaneceu em
repouso, não houve deslocamento.
•
Entre os instantes 3 s e 4 s um triângulo de área igual a
Bh
2
 4−3 .3
A2 =
2
A2=
1
www.fisicaexe.com.br
1.3
2
3
A2=
2
A 2 = 1,5
A2 =
•
Entre os instantes 4 s e 6 s um trapézio de área igual a
 Bb h
2
 43 . 6−4 
A3 =
2
7.2
A3 =
2
A3= 7
A3 =
•
Entre os instantes 6 s e 7 s um retângulo de área igual a
A 4 = L1 L2
A 4 = 4. 7−6 
A 4 = 4.1
A4 = 4
•
Entre os instantes 7 s e 9 s um trapézio de área igual a
 Bb h
2
 42 .  9−7 
A5 =
2
6.2
A5=
2
A5= 6
A5 =
O espaço percorrido será a área total dada pela soma das áreas encontradas
Δ S = A 1 A 2 A 3  A 4 A 5
Δ S = 0,51,5746
Δ S = 19 m
b) A velocidade média é dada por
v m=
ΔS
Δt
usando o espaço percorrido encontrado no item (a), temos
19
9−1
19
vm=
8
v m=
v m ≈ 2,4 m/s
c) A aceleração média é dada por
2
www.fisicaexe.com.br
am =
Δv
Δt
do gráfico temos que para t 1 = 1 s a velocidade vale v 1 = 1 m/s e para t 2 = 9 s a
velocidade vale v 2 = 2 m/s
2−1
9−1
1
am=
8
am =
a m ≈ 0,1 m/s
3
2