Física - Mecânica Clássica

nwww.fisicaexe.com.br
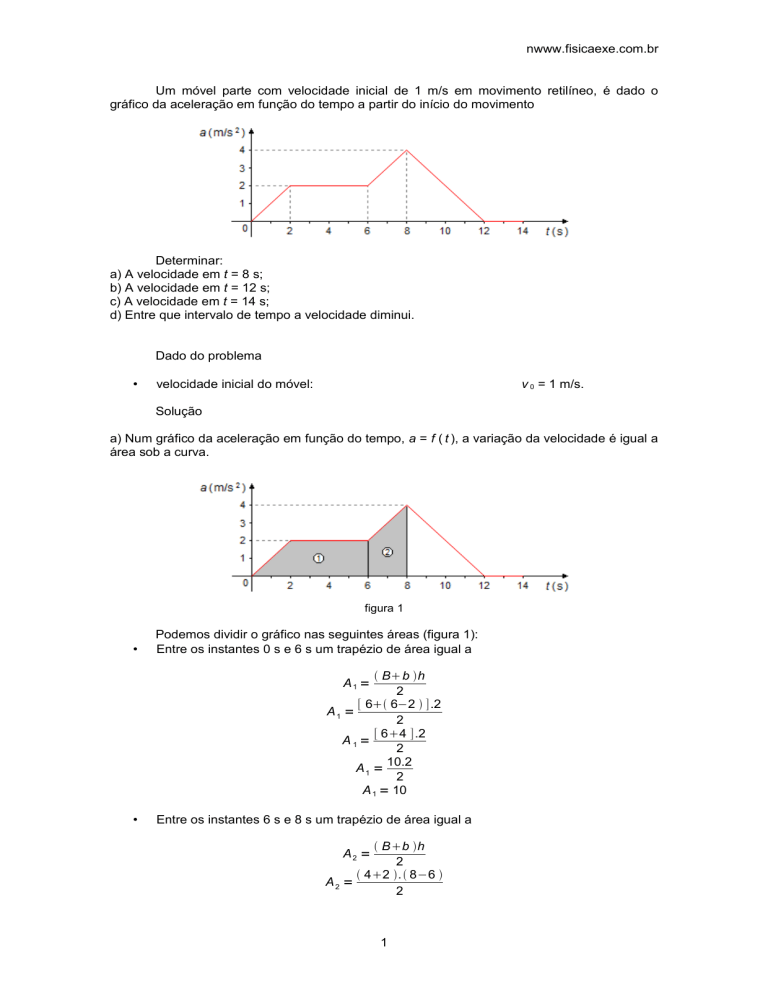
Um móvel parte com velocidade inicial de 1 m/s em movimento retilíneo, é dado o
gráfico da aceleração em função do tempo a partir do início do movimento
Determinar:
a) A velocidade em t = 8 s;
b) A velocidade em t = 12 s;
c) A velocidade em t = 14 s;
d) Entre que intervalo de tempo a velocidade diminui.
Dado do problema
•
velocidade inicial do móvel:
v 0 = 1 m/s.
Solução
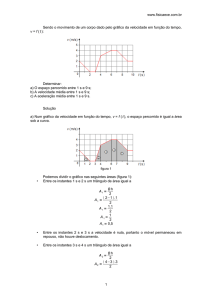
a) Num gráfico da aceleração em função do tempo, a = f ( t ), a variação da velocidade é igual a
área sob a curva.
figura 1
•
Podemos dividir o gráfico nas seguintes áreas (figura 1):
Entre os instantes 0 s e 6 s um trapézio de área igual a
 B b h
2
[ 6 6−2  ].2
A1 =
2
[ 64 ].2
A1=
2
10.2
A1 =
2
A 1 = 10
A1 =
•
Entre os instantes 6 s e 8 s um trapézio de área igual a
 Bb h
2
 42 .  8−6 
A2 =
2
A2 =
1
nwww.fisicaexe.com.br
6.2
2
A2 = 6
A2 =
A variação da velocidade será a área total dada pela soma das áreas encontradas
Δ v = A 1 A 2
Δ v = 106
Δ v = 16 m/s
Da definição de variação da velocidade temos
Δ v = ∣ v f −v i ∣
(I)
usando a variação da velocidade encontrada acima e a velocidade inicial dada no problema
( v i = v 0 = 1 m/s ), a velocidade em t = 8 s será
16 =∣ v 8 −1 ∣
16 = v 8 −1
v 8 = 161
v 8 = 17 m/s
b) Para encontrar a velocidade em t = 12 s devemos encontrar a variação da velocidade entre
t = 8 s e t = 12 s (figura 2).
figura 2
•
Entre os instantes 8 s e 12 s um triângulo de área igual a
Bh
2
 12−8 .4
A3 =
2
4.4
A3=
2
A3= 8
A3 =
Sendo esta área igual a variação da velocidade (Δ v) e a velocidade encontrada no item
(a) como sendo a velocidade inicial desta parte do movimento ( v i = v 8 = 17 m/s ), a expressão
(I) nos fornece
8 = ∣ v 12−17∣
8 = v 12−17
v 12 = 817
v 12 = 25 m/s
2
nwww.fisicaexe.com.br
c) Entre 12 s e 14 s a aceleração é nula (a = 0), portanto não há mudança na velocidade do
móvel, sua velocidade permanece constante.
d) A velocidade não diminui em nenhum intervalo de tempo.
Observação: entre os instantes 8 s e 12 s o gráfico apresenta uma reta em que a aceleração
diminui com o tempo. Mas isto não significa que a velocidade diminua, a reta está acima do
eixo das abscissas (eixo do tempo) assim a aceleração tem valor positivo (a > 0) e a velocidade
aumenta numa taxa menor. Para que a a velocidade diminuísse seria necessário que a reta
estivesse abaixo do eixo das abscissas, a aceleração teria valor negativo (a < 0) e o móvel
estaria sendo freado.
3