ANÁLISE DE MOVIMENTO RELATIVO USANDO UM SISTEMA DE

ANÁLISE DE MOVIMENTO RELATIVO
USANDO UM SISTEMA DE EIXOS EM ROTAÇÃO (Sec. 16.8)
Na descrição dos movimentos de pontos de um único corpo rígido, ou de
pontos em corpos rígidos articulados, as análises de velocidade e aceleração
relativas são feitas, como já exposto, por
um sistema auxiliar de eixos em translação.
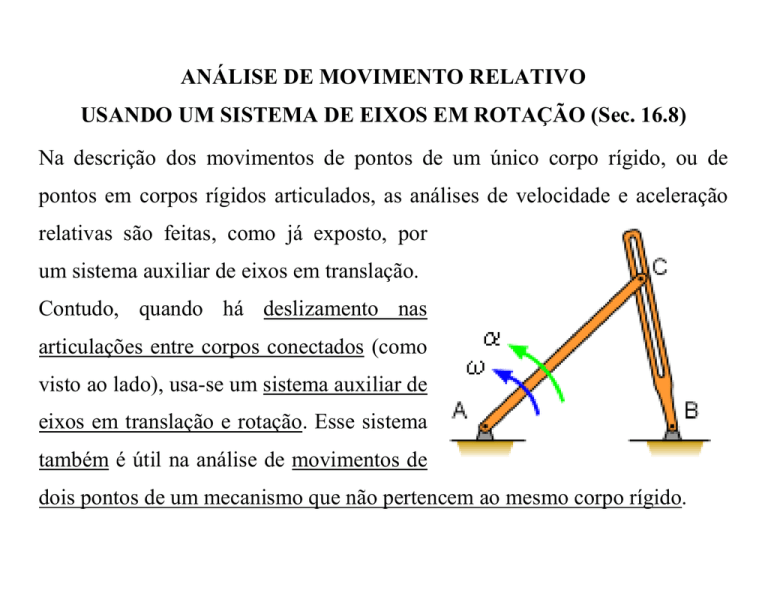
Contudo, quando há deslizamento nas
articulações entre corpos conectados (como
visto ao lado), usa-se um sistema auxiliar de
eixos em translação e rotação. Esse sistema
também é útil na análise de movimentos de
dois pontos de um mecanismo que não pertencem ao mesmo corpo rígido.
APLICAÇÃO
Uma aplicação particular é a da rotação da caçamba de um caminhão, que
ocorre em torno do pino C, por meio do avanço do cilindro hidráulico AB.
Para determinar essa rotação, é conveniente empregar equações de movimento
relativo em que um sistema auxiliar de
eixos (x,y) é fixado no cilindro. Dessa
forma, o movimento relativo de avanço
ocorrerá sempre ao longo do eixo y.
Nas análises que se seguem, de caráter
mais geral, serão obtidas duas equações,
que associam velocidades e acelerações de dois pontos, sendo um deles a
origem de um sistema de referência em translação e rotação no plano.
ANÁLISE DE POSIÇÃO
Sejam os pontos A e B na figura abaixo. Suas posições são dadas pelos
vetores de posição absoluta rA e rB, em um sistema fixo de coordenadas
(X,Y,Z). O ‘ponto de base’ A é a origem de um sistema móvel de coordenadas
(x,y,z), que está em translação e rotação em relação ao sistema (X,Y,Z), com
velocidade e aceleração angulares
dadas por ω e α ( = dω/dt). A posição
de B em relação a A é dada pelo
vetor de posição relativa rB/A. Assim,
rB = rA + rB/A (1)
em que rB/A , no sistema (x,y,z), é
rB/A = xBi + yBj (2)
ANÁLISE DE VELOCIDADE
A velocidade do ponto B é determinada derivando a Eq. (1), tal que
vB = vA + d(rB/A)/dt (3)
Uma vez que, da Eq. (2), rB/A = xBi + yBj , decorre que
drB/A d
dx B
di dy B
dj
(4)
=  x B i + y B j =
i + xB +
j + yB
dt
dt
dt
dt dt
dt
Levando a Eq. (4) na Eq. (3), tem-se que
dy B
 dx B
vB = vA + 
i+
dt
 dt
dj 
  di
j  +  x B + yB  (5)
dt 
  dt
Os termos (dxB/dt)i e (dyB/dt)j são os componentes da velocidade de B em
relação a A e são denotados, em conjunto, por (vB/A).
ANÁLISE DE VELOCIDADE (cont.)
Como os vetores i e j, do sistema (x,y,z), podem girar, suas derivadas
temporais são dadas por (vide figura ao lado)
di/dt = (dθ/dt)j = ωj = ω(k x i) (6)
dj/dt = (dθ/dt)(– i) = – ωi = ω(k x j) (7)
Das Eqs. (6), (7) e (2) em (5), resulta que
vB = vA + (vB/A) + xB(ωk) x (i) + yB(ωk) x (j)
vB = vA + (vB/A) + (ωk) x [(xB i) + (yBj)]
vB = vA + (vB/A) + (ω x rB/A) (8)
Essa é a equação da velocidade relativa via sistema em translação e rotação.
ANÁLISE DE VELOCIDADE (cont.)
Os termos à direita da equação de velocidade relativa via sistema de eixos em
translação e rotação, que é dada por
vB = vA + (vB/A) + (ω x rB/A) (8)
são representados graficamente ao
lado, de forma esquemática.
Os termos (vA) e (ω x rB/A)
relacionam o sistema (x,y,z), que
translada e gira, com o sistema
(X,Y,Z), que é fixo. A seguir, na
análise de aceleração, esses termos estarão, por conveniência, em sequência.
ANÁLISE DE ACELERAÇÃO
Sabe-se que a velocidade do ponto B é dada por
vB = vA + (ω x rB/A) + (vB/A)
(8)
Portanto, a aceleração do ponto B é obtida pela derivada da equação acima, ou
aB = aA + (dω/dt) x rB/A + ω x (drB/A/dt) + d(vB/A)/dt (9)
Como já exposto, dω/dt é a aceleração angular do sistema (x,y,z), ou seja, α.
Das Eqs. (3) e (8), sabe-se que a derivada temporal do vetor rB/A é
d(rB/A)/dt = (vB/A) + (ω x rB/A) (10)
Quanto ao vetor (vB/A), tem-se, da Eq. (5), que sua derivada temporal é tal que
d( v B/A ) d  dx B
dy B
= 
i+
dt
dt  dt
dt
2
d2 yB
  d xB
j =  2 i + 2
dt
  dt
  dx B di dy B dj 
j + 
+
 (11)
  dt dt dt dt 
ANÁLISE DE ACELERAÇÃO (cont.)
Os dois primeiros termos do lado direito da Eq. (11), qual seja
d( v B/A )  d 2 x B
d 2 yB
= 2 i+ 2
dt
dt
 dt
  dx B di dy B dj 
j + 
+
 (11)
  dt dt dt dt 
são os componentes da aceleração de B em relação a A e são denotados, em
conjunto, por (aB/A).
Em relação aos outros dois termos, tem-se, das Eqs. (6), (7) e (5), que
dxB di dyB dj dxB
dyB
 dxB dyB 
+
=
(ωk)× i +
(ωk)× j = (ωk)×
i+
j = ω×(vB/A ) (12)
dt dt dt dt dt
dt
dt 
 dt
Dessa forma,
d( v B/A )
= (a B/A ) + ω × ( v B/A ) (13)
dt
ANÁLISE DE ACELERAÇÃO (cont.)
Substituindo na Eq. (9), qual seja,
aB = aA + (dω/dt) x rB/A + ω x (drB/A/dt) + d(vB/A)/dt (9)
as Eqs. (10) e (13) e recordando que α = dω/dt, obtém-se
aB = aA + α x rB/A + ω x (vB/A) + ω x (ω x rB/A) + (aB/A) + ω x (vB/A) (14)
Reunindo os termos comuns, tem-se que
aB = aA + α x rB/A + 2ω x (vB/A) + ω x (ω x rB/A) + (aB/A)
(15)
Essa é a equação da aceleração relativa via sistema em translação e rotação.
O termo [2ω x (vB/A)] é denominado aceleração de Coriolis e sempre deve ser
considerado quando referenciais em rotação são utilizados.
ANÁLISE DE ACELERAÇÃO (cont.)
Os termos à direita da equação de aceleração relativa via sistema de eixos em
rotação, a saber,
aB = aA + α x rB/A + 2ω x (vB/A) + ω x (ω x rB/A) + (aB/A) (15)
são
representados
graficamente,
em
forma esquemática, na figura ao lado.
Observa-se que, face à generalidade das
análises apresentadas acima, os pontos A
e B poderão, ou não, possuir movimentos
independentes. Ou seja, as equações (8) e
(15) englobam todos os casos já vistos.
EXEMPLO
No mecanismo da figura ao lado, as
barras AB e DE são rotuladas por pino
nas
extremidades
A
e
D,
respectivamente, e unidas por uma
junta deslizante nas duas outras
extremidades. A junta pode se mover
livremente ao longo da barra DE, mas
se encontra articulada à barra AB em C, por um pino. Como indicado, quando
θ = 45o, a barra AB gira com velocidade angular ωAB = 4 rad/s e aceleração
angular αAB = 5 rad/s2. Nesse instante, quais são: (a) a velocidade angular da
barra DE e (b) a aceleração angular da barra DE?
Solução:
Como a distância entre os pontos D e C
varia, adota-se um sistema fixo (X,Y,Z)
e um sistema auxiliar rotativo (x,y,z),
que gira junto com a barra DE. Nota-se
que, no instante em tela, todos os vetores
serão expressos em termos de (x,y,z).
Velocidades
Primeiro, são determinadas a velocidade relativa do ponto C, (vC/D), e a
velocidade angular da barra DE, ωDE.
Pela equação da velocidade relativa via referencial rotativo, tem-se que
vC = vD + ωDE x rC/D + (vC/D) (i)
Solução (cont.):
Sabe-se que vD = 0 e que, no instante desejado, rC/D = 0,5i m.
Como a distância entre A a C não se altera, a velocidade absoluta de C pode
ser determinada a partir da barra AB, em que ωAB = – 4k rad/s, de modo que
vC = ωAB × rC/A = – 4k x (0,5i + 0,5j)
= (2i – 2j) m/s (ii)
Levando todas as informações na equação
(i), decorre que
2i – 2j = 0 + (ωDEk) x (0,5i) + (vC/D)i
2i – 2j = 0,5ωDE j + (vC/D)i (iii)
Igualando os termos em i e j, encontra-se (vC/D) = 2i m/s e ωDE =  4k rad/s .
Solução (cont.):
Acelerações
Pela equação da aceleração relativa via referencial rotativo, decorre que
aC = aD + αDE x rC/D + 2ωDE x (vC/D) + ωDE x (ωDE x rC/D) + (aC/D) (iv)
onde, para o instante desejado, tem-se, além de aD = 0, que
rC/D = 0,5i m ;
αDE x rC/D = (αDEk) x 0,5i = 0,5 αDE j m/s2 ;
2ωDE x (vC/D) = 2 (– 4k) x 2i = – 16j m/s2 ;
ωDE x ( ωDE x rC/D) = (– 4k) x [ – (4k) x (0,5 i)] = – 8i rad/s ;
(aC/D) = (aC/D) i .
Solução (cont.):
Quanto à aceleração de C, ela pode ser determinada a partir da barra AB por
aC = αAB x rC/A – ω2 rC/A
= – 5k x (0,5i + 0,5j) – (4)2 (0,5i + 0,5j)
= – 5,5i – 10,5j m/s2 (v)
Levando todas as informações acima na
equação (iv), obtém-se
– 5,5i – 10,5j = 0 + 0,5αDEj – 16j – 8i + (aC/D)i
Igualando os termos em i e j, resulta que
(aC/D) = 2,5i m/s2 e αDE = 11k rad/s2 .
EXERCÍCIO
O mecanismo de ‘retorno rápido’ da
figura ao lado consiste da manivela
AB, do bloco deslizante B e do
membro com ranhura CD. Se a
manivela tem o movimento angular
mostrado, determinar o movimento
angular do membro com ranhura nesse
instante.
Por
movimento
angular,
entende-se a velocidade e a aceleração
angulares. (Hibbeler, 12ª. ed., 16-158)
Referências:
 Dinâmica – Mecânica para Engenharia (12ª. edição), R. C. Hibbeler,
Pearson Prentice Hall, 2011;
 eCourses Dynamics – Multimedia Engineering Dynamics, K. Grammoll,
https://ecourses.ou.edu/cgi-bin/ebook.cgi?doc=&topic=dy&chap_sec=05.0.
Acessado em novembro de 2011.