Probabilidade: como medir e gerenciar a incerteza? Introduç˜ao Os

Propaganda

Probabilidade: como medir e gerenciar a
incerteza?
Introdução
Os jornais informaram que há uma chance de
60% de chover no próximo fim de semana no
Rio. Talvez seja melhor programar um cinema
em vez de programar uma ida à praia.
O noticiário da TV informou que a partir do
inı́cio de setembro haverá uma mudança no
trânsito do Rio devido às obras do novo acesso
ao centro. Como eu passo pelo local da obra
diariamente, talvez seja melhor sair de casa um
pouco mais cedo para evitar grandes engarrafamentos decorrentes da nova mudança.
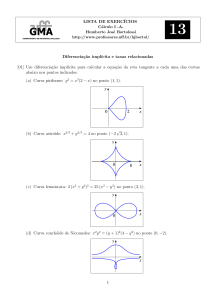
1
A nossa vida é cercada de incerteza: uma pequena chance disso, uma grande chance daquilo, etc.
Os conceitos de probabilidade, esperança (valor
esperado), retorno e possibilidade não são apenas para jogadores, são ferramentas práticas
que podemos usar para avaliar riscos, determinar opções preferidas e avaliar potenciais impactos de certas decisões.
2
PROBABILIDADE
Já vimos como analisar um conjunto de dados
por meio de técnicas gráficas e numéricas.
O resultado da análise nos permite ter uma boa
ideia da distribuição desse conjunto de dados,
em outras palavras, de como esses dados são
gerados.
Em particular, a distribuição de frequências
é um instrumento importante para avaliar a
variabilidade das observações de um fenômeno
aleatório.
As frequências relativas observadas podem ser
olhadas como estimativas de probabilidades de
ocorrência de certos eventos de interesse.
3
Com suposições adequadas, e sem observarmos diretamente o fenômeno aleatório de interesse, podemos propor um modelo teórico
que reproduza de maneira razoável a distribuição das frequências, quando o fenômeno é observado diretamente.
Modelos Probabilı́sticos
Tais modelos devem, de alguma forma,
1. identificar o conjunto de resultados possı́veis do fenômeno aleatório, que costumamos
chamar de espaço amostral, em geral denotado por S e
2. designar chances (probabilidades) aos resultados ou conjuntos de resultados possı́veis.
4
O conceito de probabilidade nos auxilia na quantificação da incerteza associada aos fenômenos
aleatórios, ou seja aos fenômenos cujos resultados não são conhecidos previamente a sua
realização/observação.
Na aula de hoje discutiremos conceitos relacionados à incerteza e veremos
• como calcular probabilidades de eventos
compostos tais como a probabilidade de
chover hoje ou amanhã e a probabilidade
de chover hoje e amanhã;
• uma ferramenta simples, mas poderosa, a
árvore de probabilidade, muito útil para resolver problemas de cálculo de probabilidades;
5
Também veremos
• uma formalização de modo a propor modelos probabilı́sticos usando o conceito de
variável aleatória;
• como calcular o valor esperado e a variância
de uma variável aleatória discreta;
• o modelo binomial;
• o modelo normal.
6
Chamamos evento a qualquer subconjunto do
espaço amostral (S). Os eventos são geralmente denotados por letras maiúsculas A, B,
etc.
Em particular chamamos o conjunto vazio (∅)
de evento impossı́vel, pois ele nunca ocorrerá
e, o espaço amostral (S), de evento certo, pois
sempre ocorrerá um dos resultados possı́veis.
Para o evento impossı́vel designamos uma probabilidade nula e para o evento certo designamos uma probabilidade igual a 1 (ou 100%).
Vamos começar a discussão com um exemplo
clássico: o lançamento de uma moeda. Temse dois resultados possı́veis: cara ou coroa.
Mas, não sabemos qual deles irá ocorrer.
7
A chance, ou probabilidade, de obter cara pode
ser pensada como a mesma de obter coroa, se
a moeda for balanceada e, desse modo podemos atribuir 50% de chance a cada resultado
possı́vel. (Interpretação clássica da probabilidade)
Por outro lado podemos desconfiar da honestidade da moeda. Uma maneira de designar a
probabilidade de cara é, por exemplo, realizar
um grande número de repetições do lançamento da moeda e ir atualizando a frequência relativa de ocorrência do número de caras. Depois de muitas realizações, podemos atribuir a
chance de “ocorrer cara” à frequência relativa
final. (Interpretação frequentista da probabilidade.)
Veja nos gráficos a seguir simulações desse
experimento com 100 lançamentos e 10000
lançamentos.
8
9
10
Interpretações da probabilidade
1) Clássica.
Baseia-se em espaços amostrais finitos e equiprováveis.
Problemas com esta interpretação:
Nem todos os espaços amostrais são finitos.
Há espaços amostrais finitos que não são equiprováveis.
Baseia-se na ideia de probabilidade (equiprovável) para definir probabilidade.
Essa interpretação no entanto é muito útil em
determinados experimentos aleatórios tais como o lançamento de uma moeda, o lançamento de cinco dados, o sorteio de uma carta de
baralho, etc.
11
Exemplo: Você está pensando em apostar no
número 13 no próximo giro de roleta. Qual é
a probabilidade de que você perca?
Uma roleta tem 38 fendas, das quais somente
uma tem o número 13. A roleta é construı́da
de tal modo que as 38 fendas sejam igualmente
prováveis. Dentre as 38 fendas, há 37 que
resultam em uma perda. Logo, a probabilidade de perder nesse caso é, sendo A o evento
“perder”
37
P (A) =
38
12
2) Frequentista
Para avaliar a probabilidade de um determinado evento de interesse, o experimento é realizado um grande número de vezes, sob as
mesmas condições. A cada realização vamos
calculando a frequência relativa de ocorrência
do evento A, como fizemos no exemplo anterior “Cara ou Coroa?”. Associamos como a
probabilidade do evento A, a frequência relativa de ocorrência do evento A após muitas
repetições.
No exemplo “Cara ou Coroa?”, o gráfico com
as frequências relativas ao longo das repetições
indica que tendemos para o valor 0,5 como
probabilidade de ocorrer cara.
Problemas com esta interpretação:
Não define com clareza o que é um grande
número de vezes, nem o que significa “sob as
mesmas condições”.
13
Nem todo fenômeno aleatório pode ser observado mais de uma vez.
Essa interpretação de probabilidade é usada na
Inferência Clássica.
Exemplo: Calcule a probabilidade de que uma
pessoa adulta escolhida ao acaso tenha voado
em um avião comercial.
O espaço amostral, considerando a observação
de cada adulto, pode ser olhado como binário
com os resultados “sucesso” e “fracasso” em
que sucesso representa que a pessoa voou em
avião comercial e fracasso que não voou. Observe que esses eventos não são necessariamente igualmente prováveis.
Aqui podemos usar a interpretação frequentista baseando-nos em alguma pesquisa.
14
Suponha que uma pesquisa observou que entre 900 adultos escolhidos ao acaso, 750 confirmaram ter voado em avião comercial. Nesse
caso, nossa resposta, baseada na frequência
relativa, para o evento A: “ter voado em avião
comercial” é
750
P (A) =
' 0, 833.
900
15
3) Subjetiva. O indivı́duo, baseado em informações anteriores e na sua opinião pessoal
a respeito do evento em questão, pode ter uma
resposta para a probabilidade desse evento.
O ingrediente básico quando se associam probabilidades é coerência. Se um indivı́duo julgar
que um evento A é mais provável que o seu
complementar, então ele deverá associar a esse
evento uma probabilidade maior do que 50%
ao evento A.
Problemas com essa interpretação: Pesquisadores diferentes podem associar probabilidades
diferentes para um mesmo evento!
16
A Inferência Bayesiana toma como uma de
suas bases o fato de que todas as probabilidades são subjetivas.
Exemplo: Qual é a probabilidade de que seu
carro seja atingido por um meteorito em 2013?
Na ausência de dados históricos sobre meteoritos colidindo com carros, não podemos usar
a interpretação frequentista. Observe que há
dois resultados possı́veis nesse problema:
{colidir, não colidir},
mas eles não são igualmente prováveis de modo
que não podemos usar a interpretação clássica
de probabilidade.
17
Observe que nesse exemplo podemos fazer uso
da interpretação subjetiva. Todos nós sabemos que a probabilidade em questão é muito
pequena. Vamos então estimá-la em
1
= 10−12
1000000000000
equivalente a 1 em um trihão.
Esta estimativa subjetiva, baseada em nosso
conhecimento geral, é bem provável que esteja
perto da verdadeira probabilidade.
18
19
Definição Axiomática da Probabilidade
A Axiomatização da Probabilidade é devida ao
matemático russo Kolmogorov e ocorreu no
inı́cio do Século XX.
Independentemente da interpretação de probabilidade adotada, a probabilidade é uma função P (.) que mede chances de eventos. A
função probabilidade está definida na coleção
de eventos e assume valores entre 0 e 1, satisfazendo os seguintes axiomas:
A1 : P (A) ≥ 0 para todo evento A na coleção
de eventos. A probabilidade de um evento
qualquer é sempre um número não-negativo.
A2 : P (S) = 1. A probabilidade do evento
certo é igual a 1.
A3 : Se A ∩ B = ∅, então P (A ∪ B) = P (A) + P (B).
Se os eventos A e B são disjuntos, então a probabilidade
da união dos dois (de pelo menos um deles ocorrer) é a
soma de suas probabilidades.
20
Propriedades da probabilidade
A partir dos axiomas, diversas propriedades da
probabilidade podem ser deduzidas.
P 1 : P (∅) = 0
P 2 : Se A ⊂ B, então P (A) ≤ P (B).
P 3 : 0 ≤ P (A) ≤ 1, para todo evento A.
P 4 : Propriedade do evento complementar de
A: Ac
Ac = S \ A = {s ∈ S|s 6∈ A}
P (Ac) = 1 − P (A)
21
Eventos União e Interseção de dois eventos
Considere um experimento aleatório e sejam
A e B dois eventos associados a esse experimento.
O evento união de A e B, denotado por
A ∪ B, corresponde ao evento “ocorrência de
pelo menos um dos dois A ou B”
O evento interseção de A e B, denotado por
A ∩ B, corresponde ao evento “ocorrência simultânea de A e B”.
22
Esses dois eventos, chamados de eventos compostos, pois são obtidos por meio de operações
entre dois ou mais eventos, são diferentes. Enquanto o evento união de A e B representa a
ocorrência de pelo menos um, o que significa
que poderá ter ocorrido somente A, somente
B ou os dois simultaneamente; o evento interseção corresponde a ocorrência dos dois simultaneamente.
Observe que como A ∩ B ⊂ A ∪ B segue que
P (A ∩ B) ≤ P (A ∪ B).
A igualdade é possı́vel? Sob que condição?
23
Veremos a seguir uma propriedade útil para
calcular a probabilidade da união de dois eventos.
P 5 : P (A ∪ B) = P (A) + P (B) − P (A ∩ B).
Um caso particular ocorre quando A ∩ B = ∅,
pois nesse caso P (A ∩ B) = 0 e
P (A ∪ B) = P (A) + P (B).
Mas lembre-se que essa última equação só vale
se a interseção entre os eventos A e B for
vazia.
24
Probabilidades Condicionais
Suponha que num dado problema de modelagem probabilı́stica, embora você não conheça
o resultado do fenômeno sob estudo, seja possı́vel ter informações acerca do resultado. Por
exemplo, ao lançar um dado, embora o valor
da face obtida seja desconhecido, você receba
a informação de que esse valor é um número
ı́mpar.
Como ficam as probabilidades associadas a um
evento de interesse nesse caso? Suponha por
exemplo que o evento de interesse seja obter
face “6”.
Dado que nós temos informações sobre o resultado faz sentido atualizarmos as nossas incertezas a cerca do evento de interesse.
25
Probabilidade Condicional: Definição
A probabilidade condicional de ocorrer um evento A, dado que sabemos que ocorreu um
evento B, P (B) > 0 é definida por
P (A|B) =
P (A ∩ B)
.
P (B)
Probabilidades condicionais têm um espaço amostral reduzido, pois só nos preocupamos com
os resultados baseados no que já aconteceu.
Essa definição é útil para designar uma forma
de obter probabilidades de eventos interseção
de dois eventos, a saber,
P (A ∩ B) = P (A|B) × P (B)
→ regra da multiplicação ←
26
Exemplo: Numa turma de 20 alunos da disciplina Estatı́stica em um curso de Graduação,
15 são mulheres e 5 são homens. Dois alunos
dessa turma serão sorteados ao acaso, e sem
reposição, de modo a formar uma comissão de
representantes da turma. Pede-se calcular a
probabilidade de que ambos sejam do mesmo
gênero.
Solução: Vamos chamar de evento Ai o evento
“a i-ésima pessoa sorteada é do gênero feminino”, i = 1, 2, pois são apenas dois sorteios.
O evento desejado, vamos chamar de evento
E, ambos do mesmo gênero, é um evento composto:
E=
(A ∩ A )
| 1 {z 2 }
ambas mulheres
∪ (Ac1 ∩ Ac2)
|
{z
}
ambos homens
Como A1 ∩ A2 e Ac1 ∩ Ac2 são disjuntos, segue
que P (E) = P (A1 ∩ A2) + P (Ac1 ∩ Ac2).
27
Usando a regra da multiplicação temos
P (A1 ∩ A2) =
prob. do seg. ser mulher se prim. é mulher
=
×
P (A )
| {z 1 }
z
}|
{
P (A2|A1)
prob. do prim. ser mulher
15 14
21
=
×
=
20 19
38
P (Ac1∩Ac2) = P (Ac1)×P (Ac2|Ac1) =
4
2
5
×
=
20 19
38
Logo,
2
23
21
P (E) =
+
=
' 0, 605
38
38
38
28
Árvore de Probabilidades
29
Observe que no exemplo anterior os sorteios
foram realizados sem reposição de tal modo
que ao sortearmos a segunda pessoa o universo
passou a ser de 19 alunos, pois a primeira pessoa sorteada não estava entre as possibilidades
do segundo sorteio.
Como fica a solução do mesmo problema se
agora o sorteio é feito com reposição?
Suponha agora que existem dois prêmios a serem distribuı́dos ao acaso e sem restrições de
tal maneira que o primeiro sorteado também
possa receber o segundo prêmio.
Calcule a probabilidade de que os prêmios tenham sido recebidos por pessoas do mesmo
gênero: apenas mulheres foram premiadas ou
apenas homens foram premiados.
30
Árvore de Probabilidades
15 = 3 e 5 = 1 .
20
4
20
4
P (E) =
2
3
4
+
2
1
4
5
= = 0, 625
8
Podemos ver que as respostas são ligeiramente diferentes. Um resultado útil é que quando o tamanho da população amostrada tende
a ser muito maior que o tamanho da amostra, as diferenças passam a ser desprezı́veis tal que o esquema de sorteio sem reposição
poderia ser tratado como o esquema mais simples de sorteio com
reposição.
31
Eventos independentes
Dizemos que os eventos A e B são independentes, se a ocorrência de um deles, por exemplo de B, não interfere no nosso conhecimento
sobre a incerteza do outro A.
A e B são eventos independentes se
P (A|B) = P (A).
Nesse caso, observe que vale a seguinte propriedade
P (A ∩ B) = P (A) × P (B),
para A e B eventos independentes.
Cuidado: essa última expressão não é uma regra geral. É uma propriedade que vale para
eventos independentes.
32
Voltando ao exemplo anterior observe que os
eventos A1 e A2 não são independentes no caso
do sorteio sem reposição, pois P (A1 ∩ A2) 6=
P (A1)P (A2) (verifique).
No entanto, no caso do sorteio com reposição,
podemos verificar que os eventos A1 e A2 são
independentes, pois vale
P (A1 ∩ A2) = P (A1)P (A2).
Um propriedade interessante é a seguinte. Se
A e B são eventos independentes, então,
1. A e B c são eventos independentes;
2. Ac e B são eventos independentes;
3. Ac e B c são eventos independentes.
33
Eventos independentes versus Eventos disjuntos
Cuidado: É comum ocorrer confusão com o
que chamamos em probabilidade de eventos
independentes com eventos disjuntos.
São situações bem diferentes.
Se dois eventos A e B são disjuntos com
P (A) > 0 e P (B) > 0, então A e B NÃO podem ser independentes!
Por que?
Lembre: dois eventos são independentes em
probabilidade se a ocorrência de um não interfere na probabilidade de ocorrência do outro.
34
Lei dos Grandes Números (Bernoulli-século XVIII)
À medida que um experimento é repetido muitas vezes, a probabilidade dada pela frequência
relativa de um evento tende a se aproximar da
verdadeira probabilidade desse evento.
A lei dos grandes números nos diz que as estimativas de probabilidades dadas pelas frequências relativas tendem a ficar melhores com mais
observações: uma estimativa de probabilidade
baseada em poucas tentativas pode estar bem
afastada do verdadeiro valor da probabilidade,
mas com um número maior de tentativas, a
estimativa tende a ser mais precisa.
Uma pesquisa de opinião sobre a preferência pela marca
X de sabão em pó com apenas 12 donas de casa escolhidas ao acaso pode facilmente resultar em estimativas
muito afastadas da verdadeira proporção de donas de
casa que preferem a marca X. No entanto, se entrevistarmos 1200 donas de casa, nossa estimativa estará
próxima da verdadeira proporção.
35
Variáveis Aleatórias
Considere um experimento cujo espaço amostral é S. O conjunto S contém todos os resultados possı́veis. Em muitas situações ele será
um conjunto cujos elementos não são números.
Por exemplo, considere o lançamento de uma
moeda duas vezes consecutivas. Nesse caso,
um espaço amostral para esse experimento é
S = {(ca, ca), (ca, co), (co, ca), (co, co)}
cujos elementos são pares contendo as entradas
ca para cara e co para coroa.
De modo bastante informal, uma variável aleatória é uma caracterı́stica numérica do resultado de um experimento.
No caso desse último exemplo, podemos definir
a variável alaetória X como o número de caras
obtidas.
36
Observe que nesse caso,
X=


 0,
1,

 2,
se ocorrer {(co, co)}
se ocorrer {(ca, co), (co, ca)}
se ocorrer {(ca, ca)}
Dizemos que o campo de definição da variável
aleatória X é o conjunto {0, 1, 2} que representa os valores que X pode assumir.
Suponha agora que estejamos interessados em
observar o tempo de vida de uma lâmpada.
Observe que antes de realizar o experimento
não é possı́vel dizer qual será a resposta. É
fácil ver que um espaço amostral para esse experimento é S = {s ∈ R|s ≥ 0}. Nesse caso
o espaço amostral já é numérico de tal forma
que podemos definir a variável aleatória como
o tempo de vida da lâmpada.
37
Dizemos que uma variável aleatória é discreta
se seu campo de definição for um conjunto
finito ou enumerável (resultante de uma contagem, mas pode ser infinito).
No caso dos exemplos anteriores a variável número de caras é discreta e a variável tempo de
vida da lâmpada não é discreta.
A seguir apresentaremos modelos Probabilı́sticos para variáveis aleatórias discretas: função
de probabilidade, função de distribuição e suas
caracterizações.
38
Função de probabilidade: associa a cada valor
possı́vel da v.a. discreta sua respectiva probabilidade.
Se RX é o campo de definição da v.a. discreta
X podemos representar sua função de probabilidade da seguinte forma
(
p(x) =
P (X = x), x ∈ RX
0,
caso contrário
Observe que P (X = x) = 0 quando x 6∈ RX ,
ou seja quando x é um valor fora do campo
de definição de X a respectiva probabilidade
é nula. Quando x ∈ RX , p(x) > 0 tal que
a função de probabilidade assume sempre valores não-negativos, isto é, p(x) ≥ 0, para todo
x. Além disso, decorre dos axiomas da probaX
bilidade que
p(x) = 1.
x∈RX
39
Observação: qualquer função p(x) satistazendo
essas duas propriedades:
P1: p(x) ≥ 0 para todo x e
P2:
X
p(x) = 1
x∈RX
é função de probabilidade para alguma v.a.
discreta X com campo de definição RX .
Função de distribuição (ou função de distribuição
acumulada)
É definida da seguinte forma
F (x) = P (X ≤ x), x ∈ R
No caso das variáveis aleatórias discretas o
gráfico da função de distribuição é uma função
do tipo escada, não decrescente. Veja um exemplo a seguir.
40
É possı́vel deduzir a partir desse gráfico que
RX = {0, 1} e que
P (X = 0) = 0, 8 e P (X = 1) = 0, 2.
Por que?
41
A função de probabilidade pode ser interpretada como um modelo teórico para uma determinada variável em estudo.
Como no caso de distribuições de frequências
empı́ricas (amostras) também podemos querer
caracterizar as distribuições de probabilidade
por meio de medidas-resumo.
O valor esperado de uma variável aleatória discreta com função de
probabilidade p(x) é defiX
nido por E[X] =
x × p(x).
x∈RX
Assim como no caso de dados amostrais, o
valor esperado representa o centro de massa
da função de probabilidade.
Considere o exemplo de lançar uma moeda
duas vezes consecutivas. Vimos que o campo
de definição da variável definida como número
de caras obtidas é {0, 1, 2}.
42
Usando o diagrama de árvore é fácil obter a
função de probabilidade.
x
0
1
2
soma
p(x)
1/4
1/2
1/4
1
43
Assim, nesse exemplo, o valor esperado do
número de caras é
1
1
1
E[X] = 0 × + 1 × + 2 × = 1
4
2
4
Que interpretação deve ser dada a esse resultado?
Podemos dizer que vamos observar uma cara
ao realizarmos esse experimento?
Na verdade o valor esperado representa uma
medida a longo prazo: se repetirmos este experimento “lançar a moeda duas vezes seguidas” muitas vezes e irmos registrando o número
de caras em cada repetição, a média do número
de caras obtidas ao longo das repetições, se
aproximará de 1, quanto maior for o número
de repetições. (Lei dos Grandes Números).
44
Vimos que além de caracterizar uma distribuição de frequências usando medidas de tendência central, também usamos medidas de dispersão. Para uma variável aleatória discreta
com função de probabilidade p(x), também faz
sentido usar a variância para caracterizar a dispersão de seus valores possı́veis em torno do
seu valor esperado.
V ar(X) =
X
x∈RX
2
(x − E[X]) ×p(x) =
X
x2 ×p(x)−(E[X])2
x∈Rx
A variância é uma medida não-negativa e quando ela é zero isso significa que não há variabilidade e no caso de uma variável aleatória
discreta significa que P (X = E[X]) = 1.
No exemplo do número de caras ao lançar uma
moeda duas vezes, tem-se V ar(X) = 1
2.
45
Existem infinitos modelos para representar a
geração de variáveis aleatórias discretas. Alguns aparecem mais frequentemente e por isso
são tratados de forma especial, tais como os
modelos binomial, geométrico, Poisson, etc.
Vamos tratar em particular do modelo binomial, um dos mais comuns.
Um Ensaio de Bernoulli é um experimento para
o qual há apenas dois resultados possı́veis que
convencionamos chamar de sucesso ou fracasso.
Aqui sucesso não precisa significar algo bom,
pode representar por exemplo, peça com defeito.
O modelo binomial ocorre quando repetimos
independentemente um número fixado de vezes,
digamos n vezes, um Ensaio de Bernoulli, cuja
probabilidade de sucesso é p, 0 < p < 1.
46
Nesse contexto definimos a variável aleatória
binomial como sendo o número de sucessos
em n ensaios de Bernoulli cuja probabilidade
de sucesso é p, 0 < p < 1.
Exemplos de situações que levam ao modelo
binomial (n, p):
• número de caras obtidas ao lançar uma
moeda 10 vezes consecutivas;
• número de faces “6” ao lançar cinco dados
balanceados;
• número de peças defeituosas ao observar
uma amostra aleatória de 25 peças produzidas pela mesma máquina;
• número de alunos que fazem aniversário no
primeiro trimestre ao observar uma amostra
aleatória de 10 alunos de uma turma.
47
Modelo Binomial
Notação: X ∼ binomial(n, p)
Campo de definição: RX = {0, 1, 2, ..., n}
Função de Probabilidade:
p(x) =



n
x
!
px(1 − p)n−x, x ∈ RX


0, caso contrário
n
x
!
n!
=
x!(n − x)!
n! = n(n − 1)...3.2.1, 0! = 1
Valor esperado: E[X] = np
Variância: V ar(X) = np(1 − p)
48
Exemplo: Das variáveis descritas a seguir, assinale quais são binomiais, e para essas apresente
os respectivos campo de definição, valor esperado e variância. Quando julgar que a variável
não é binomial, aponte as razões de sua conclusão.
1. De uma urna com 10 bolas brancas e 20 pretas, vamos extrair,
com reposição, cinco bolas. X é o número de bolas brancas
nas cinco extrações.
2. Refaça o problema anterior, mas dessa vez as extrações são
sem reposição.
3. Temos cinco urnas com bolas pretas e brancas e vamos extrair
uma bola de cada urna. X é o número de bolas brancas
obtidas no final.
4. Vamos realizar uma pesquisa em 10 cidades brasileiras, escolhendo ao acaso um habitante de cada uma delas e classificando-o como pró ou contra um certo projeto do governo
federal. X é o número de pessoas contra o projeto.
5. Numa Indústria existem 100 máquinas que fabricam uma peça.
Cada peça é classificada como boa ou defeituosa. Escolhemos
ao acaso um instante de tempo e verificamos uma peça de
cada uma das máquinas. X é o número de peças defeituosas
ao final da verificação.
49
Variáveis aleatórias contı́nuas: de modo informal as variáveis aleatórias são contı́nuas quando resultam de algum tipo de medição tal que
seu campo de definição é um intervalo limitado
da reta, uma semi-reta ou a reta.
Por exemplo: o tempo de vida de uma lâmpada,
a altura de uma pessoa, o peso de uma pessoa,
o tempo de cura após iniciar um tratamento,
etc.
O modelo probabilı́stico usual para descrever o
comportamento de variáveis aleatórias contı́nuas é a função de densidade de probabilidade ou simplesmente densidade de probabilidade.
A função de distribuição F (x) = P (X ≤ x)
também pode ser usada para descrever o comportamento de uma variável aleatória contı́nua.
50
Uma densidade de probabilidade é uma função
real, não-negativa e tal que a área delimitada
sob o gráfico da densidade é igual a 1.
O histograma costuma ser usado para através
da distribuição empı́rica dos dados amostrais,
tentar identificar um modelo teórico que descreva razoavelmente a geração deles.
51
No caso de variáveis aleatórias contı́nuas o cálculo de probabilidades para valores da variável
em intervalos do campo de definição é mais
sofisticado e o cálculo direto muitas vezes demanda conhecimentos de Cálculo Integral, que
não é um pré-requisito de Estatı́stica Aplicada
II.
No entanto, isto não impede prosseguir no estudo dos modelos probabilı́sticos para variáveis
aleatórias contı́nuas, pois na maioria das situações que iremos estudar, poderemos facilmente
obter as probabilidades solicitadas usando tabelas e programas estatı́sticos.
52
Se X é uma variável aleatória contı́nua com
densidade f (x), então a probabilidade de X
cair num intervalo entre a e b será dada pela
área delimitada pela densidade f (x) entre a e
b como mostra a figura seguir.
53
Se X é uma variável aleatória com densidade
f (x) também é possı́vel calcular o valor esperado de X e sua respectiva variância, com as
mesmas interpretações apresentadas anteriormente: o valor esperado representa um centro
de massa em relação à medida de probabilidade e a variância representa a dispersão dos
valores no campo de definição em relação à
média.
A seguir vamos apresentar o modelo normal,
fundamental em probabilidade e inferência estatı́stica. Suas origens remontam a Gauss em
seus trabalhos sobre erros de observações astronômicas, por volta de 1810, daı́ o nome que
muitas vezes aparece de distribuição gaussiana
para tal modelo.
54
Gauss levou a fama, pois foi ele o primeiro a
publicar sobre resultados práticos envolvendo a
distribuição normal. No entanto, o primeiro a
se referir a distribuição normal foi o Matemático
Francês De Moivre em 1733. De Moivre usou
a distribuição normal para aproximar probabilidades relacionadas a lançamentos de moedas,
chamou-a de curva exponencial em forma de
sino. Sua utilidade, porém, só foi tornar-se
aparente em 1809, quando o famoso matemático alemão Gauss usou-a em aplicações sobre
a observação de fenômenos astronômicos.
55
Do meio ao final do século XIX, boa parte dos
estatı́sticos começou a acreditar que a maioria dos conjuntos de dados teriam histogramas
cuja forma se adequava à forma de sino. De
fato, tornou-se aceito que era “normal” para
qualquer conjunto de dados “bem-comportados” seguir esse modelo. Ao longo do século
XX no entanto existem vários registros do mau
uso de técnicas estatı́sticas, pois saiu-se usando indiscrimidamente técnicas que pressupunham a normalidade dos dados, quando eram
claramente não normais.
Cuidado: Sempre verifique se o método de
análise estatı́stica que você irá usar é adequado
aos seus dados.
Uma explicação parcial de porque tantos conjuntos de dados conformam-se com a curva
normal é fornecida pelo teorema central do limite que enunciaremos adiante.
56
A Curva Normal (Gaussiana, Forma de Sino)
A curva normal é totalmente caracterizada por
dois parâmetros: seu valor esperado (ou sua
média), denotada pela letra grega µ e a sua
variância, denotada por σ 2 ou, equivalentemente pelo seu desvio-padrão σ.
57
Modelo Normal
Notação X ∼ N (µ, σ 2)
Campo de definição: R
Densidade:
x−µ 2
1
−2 σ
1
f (x) = √ e
σ 2π
Valor esperado: E[X] = µ
Variância: V ar(X) = σ 2.
Assimetria: zero
Curtose: 3
58
Como os parâmetros µ e σ 2 influenciam na
curva normal?
A seguir apresentamos o gráficos de duas curvas normais com a mesma variância, mas com
médias diferentes, µ1 < µ2.
Observe que a média µ caracteriza o centro do
gráfico e, dessa forma, distribuições normais
com médias diferentes, mas mesma variância
apresentam gráficos congruentes centrados em
posições diferentes.
59
Como os parâmetros µ e σ 2 influenciam na
curva normal?
A seguir apresentamos o gráficos de três curvas normais com a mesma média, mas com
variâncias diferentes, σ12 < σ22 < σ32.
Observe que a variância σ 2 caracteriza o nı́vel
de abertura do gráfico em relação ao centros e,
dessa forma, distribuições normais com variâncias diferentes, mas mesma média apresentam
gráficos centrados na mesma posição, mas com
aberturas diferentes conforme o valor da variância.
60
Na curva normal os pontos x = µ ± σ são os
pontos de inflexão, isto é, os pontos nos quais
a concavidade da curva normal se modfica.
Entre µ − σ e µ + σ a concavidade está voltada
para baixo e, fora desse intervalo a concavidade está voltada para cima.
Na curva normal a reta x = µ representa um
eixo de simetria tal que f (µ − δ) = f (µ + δ),
para todo δ ∈ R.
61
Distribuição Normal Padrão
Quando µ = 0 e σ 2 = 1 a distribuição é chamada
normal padrão ou normal reduzida.
Z ∼ N (0, 1)
Vamos usar a letra Z para denotar uma variável
aleatória normal com distribuição normal padrão.
Nesse caso, a densidade é dada por
1 − z2
fZ (z) = √ e 2 ,
2π
z∈R
E[Z] = 0 e V ar(Z) = 1.
Outra notação que será adotada aqui é
φ(z) = P (Z ≤ z),
para a função de distribuição da normal padrão.
62
Como calcular probabilidades usando o modelo
normal?
Vamos começar com a situação em que
Z ∼ N (0, 1), ou seja, em que a distribuição
considerada é uma normal padrão.
De fato, não é possı́vel calcular de forma exata probabilidades do tipo P (a < Z < b), mas
podemos obter aproximações desses valores usando métodos numéricos. No caso da distribuição normal padrão, valores de probabilidades especı́ficas são tabulados. Em quase
todos os livros de estatı́stica estão disponı́veis
tabelas da distribuição normal padrão.
63
64
A tabela anterior pode parecer incompleta, mas
ela é útil para calcular probabilidades de diversos intervalos, inclusive incluindo valores negativos em seus extremos. Isso se deve a propriedade de simetria da curva normal padrão
em torno de zero.
Cuidado: Sempre leia o cabeçalho da tabela
que você estiver usando, pois não existe uma
norma universal de apresentação de tabelas da
normal padrão. Às vezes as tabelas fornecem
probabilidades acumuladas como a que acabamos de ver, outras vezes elas trazem probabilidades da cauda inferior ou superior e outras
vezes elas fornecem probabilidades entre 0 e
um número positivo.
Usando a tabela que fornece probabilidades acumuladas da normal padrão,
φ(z) = P (Z ≤ z), vamos ver exemplos de como
obter probabilidades referentes a outros intervalos.
65
Pela tabela disponı́vel vemos diretamente que,
por exemplo,
φ(1) = P (Z ≤ 1) = 0, 8413
φ(1, 64) = P (Z ≤ 1, 64) = 0, 9495
φ(2, 33) = P (Z ≤ 2, 33) = 0, 9901
Lembre que a área total sob a curva é 1 e,
portanto, é fácil deduzir que
P (Z > 1) = 1 − φ(1) = 1 − 0, 8413 = 0, 1587
P (Z > 1, 64) = 1 − φ(1, 64) = 1 − 0, 9495 = 0, 0505
P (Z > 2, 33) = 1 − φ(2, 33) = 1 − 0, 9901 = 0, 0099
66
Observe que como a curva normal padrão é
simétrica em torno de zero, segue que
φ(−z) = 1 − φ(z), ∀z.
Logo,
φ(−1) = 1 − P (Z ≤ 1) = 0, 1587
φ(−1, 64) = 1 − P (Z ≤ 1, 64) = 0, 0505
φ(−2, 33) = 1 − P (Z ≤ 2, 33) = 0, 0099
67
Observe que
P (1 < Z < 2) = P (Z < 2) − P (Z < 1) = φ(2) − φ(1) =
0, 9773 − 0, 8413 = 0, 1360
De modo similar
P (−2 < Z < −1) = P (1 < Z < 2) = 0, 136
68
Observe que
P (−1 < Z < 2) = P (Z < 2) − P (Z < −1) e
P (Z < −1) = P (Z > 1) = 1 − P (Z ≤ 1) = 1 − φ(1)
Logo,
P (−1 < Z < 2) = φ(2) + φ(1) − 1 = 0, 9773 + 0, 8413 − 1 = 0, 8186
No caso da normal padrão observe que para intervalos simétricos
em torno de zero vale
P (−c < Z < c) = 2φ(c) − 1 e, a probabilidade das caudas,
P (|Z| > c) = 2 (1 − φ(c)).
69
Logo, apesar da tabela parecer ser limitada, vimos que é possı́vel calcular, via aproximações,
probabilidades associadas a uma variável aleatória com distribuição normal padrão para quaisquer intervalos fixados.
No entanto, na prática, as variáveis em questão, apesar de serem consideradas normais,
certamente não terão média zero e variância
um.
Como calcular probabilidades no caso de uma
distribuição normal qualquer?
Uma propriedade importante das curvas normais, independentemente de sua média e seu
desvio-padrão, está ilustrada na figura a seguir.
70
71
Trasnformação de Padronização
Um resultado importante que vale para a distribuição normal é que ao efetuarmos transformações afins numa variável aleatória normal, a variável transformada continua sendo
uma variável normal, isto é se X é normal e
definimos Y = aX + b, com a 6= 0, então Y
também é normal.
72
Para relacionar uma normal qualquer à normal
padrão temos o seguinte resultado
1. se X ∼ N (µ, σ 2), então
Z=
X −µ
σ }
| {z
∼ N (0, 1)
transf. de padronização
Essa relação torna possı́vel calcular probabilidades associadas a uma variável normal qualquer, transformando-a numa normal padrão.
2. se Z ∼ N (0, 1), então X = σZ+µ ∼ N (µ, σ 2).
Podemos usar qualquer uma das relações.
73
Discussão Técnica sobre QI
Fonte: http://www.mensa.com.br/pag.php?p=23.
Origem da ideia do Quociente de Inteligência (QI)
O psicólogo francês Alfred Binet foi um dos precursores do estudo da inteligência humana e idealizou testes
para medi-la e, com isso, tentar melhorar o desempenho escolar das crianças. A inteligência humana,
como outras caracterı́sticas fı́sicas e psicológicas, tem
grande variação dentro dos indivı́duos. É natural, portanto, que existam pessoas mais, e menos, inteligentes.
Conhecendo-se esta caracterı́stica pode-se acompanhar
melhor cada criança em sua vida acadêmica.
A idéia original do teste de QI de Binet seria comparar
a idade cronológica com a idade intelectual. Por comodidade definiu-se que o QI médio sempre vale 100
pontos.
Uma criança, digamos com 5 anos de idade, que apresentasse um QI de 120 teria, portanto, uma idade intelectual 20% acima da inteligência média das crianças
com 5 anos de idade, ou seja, esta criança teria uma
idade intelectual média equivalente à de uma criança de
6 anos de idade.
No caso de adultos, entretanto, faz muito pouco sentido
dizer que uma pessoa com idade de 40 anos tem a idade
intelectual de um adulto de 48 anos.
74
O valor do QI, para adultos, passa a ser pouco significativo e, em geral, é melhor classificar a inteligência
em termos de porcentagem.
É mais informativo dizer que uma pessoa tem uma inteligência maior do que, por exemplo, 98% da população
(ou seja, a inteligência desta pessoa está entre os 2%
mais inteligentes da população) do que dizer que o QI
é, por exemplo, 148.
A seguir discussão sobre o QI refere-se ao QI adulto.
Acredita-se que a distribuição de QI na população tenha
uma função densidade de probabilidade normal. Vimos
que para especificar completamente uma distribuição
normal é necessário fixar o valor dos parâmetros: média
e desvio padrão.
Por convenção, como já comentado, a média é sempre
fixada como 100. Para “converter” um QI em uma
porcentagem (ou vice-versa) é sempre necessário que
se conheça o desvio padrão. Não tem sentido falar em
QI (numérico) sem citar, também, qual desvio padrão
está sendo utilizado.
75
Há diversos testes de QI e cada um deles foi
calibrado (empiricamente) para um valor de
desvio padrão. Há, por exemplo, testes famosos
com desvios de 15, 16 e 24. Note que há muita
diferença entre estes desvios e, consequentemente, a conversão entre QI e porcentagem é
bastante diferente em cada caso.
O QI informado pela Mensa, no resultado de
seus testes, tem desvio padrão 24.
Uma pessoa com QI topo 2% pode ter um QI
numérico maior ou igual a 130(131) se d.p.=15,
132(133) se d.p.=16 ou 148(149) se d.p. 24.
Observe que isso equivale a dizer dois desvios
padrão acima da média (2,05 desvios a cima
da média).
As figuras a seguir ilustram a distribuição de
QI com os três desvios citados.
76
77
Exemplo: Supondo uma distribuição N (100, 242)
para o QI, responda aos itens a seguir.
Determine a probabilidade de que uma pessoa
submetida ao teste apresnte QI
1. maior ou igual a 148;
2. menor que 76;
3. entre 80 e 120;
4. entre 120 e 148.
5. Calcule os quartis da distribuição do QI.
6. Encontre um intervalo simétrico em torno
da média 100, que compreenda 95% dos
resultados desse teste.
78
Solução do item (1)
Temos que X ∼ N (100, 242) e queremos calcular (X ≥ 148).
Observe que
P (X ≥ 148) = 1 − P (X < 148)
P (X < 148) = P
0, 9773
X−100
24
<
148−100
24
= P (Z < 2) = φ(2) =
Logo, P (Z ≥ 1148) = 1 − 0, 9773 = 0, 0227 ou, equivalentemente, 2,27%.
Observe não é possı́vel encontrar um valor de QI inteiro
n tal que P (X ≥ n) = 0, 02.
Vamos tentar resolver esse problema
n =? tal que P (X ≥ 2) = 0, 02
n−100
Nesse caso, φ 24
= 0, 98.
79
Não há na tabela um valor exatamente igual
a 0,98 e devemos usar o valor mais próximo.
Podemos ver que na tabela disponı́vel o valor
que associa a probabilidade acumulada mais
próxima de 98% é 2,05. Logo,
n−100 = 2, 05 tal que n = 149, 2.
24
De fato, a resposta maior ou igual a 149 para
QI topo seria mais apropriada. No entanto,
costuma-se adotar certas aproximações para
distribuições normais: a cauda superior, dois
desvios padrão acima da média corresponde a
aproximadamente 2% da distribuição.
Vimos, usando a tabela, que é cerca de 2,27%,
mas para facilitar é hábito arredondar para 2%.
80
Referências bibliográficas:
(1) Busssab e Morettin - Estatı́stica Básica.
Editora Saraiva
(2) Triola, M. - Introdução à Estatı́stica - LTC
(3) Thurman - Estatı́stica - Saraiva
(4) Pinheiro e outros - Estatı́stica Básica - a
arte de trabalhar com dados - Elsevier
(5) Ross, S. - A First Course in Probability Prentice-Hall
(6) Dancey e Reidy - Estatı́stica sem Matemática
para Psicologia - Penso
(7) http://www.mensa.com.br/pag.php?p=23.
Em 28/08/2013
81