CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ www

CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
Olá pessoal!
Esta é a nossa última aula de Raciocínio Lógico.
Aula 5: Geometria plana: distâncias e ângulos, polígonos, circunferência,
perímetro e área. Semelhança e relações métricas no triângulo retângulo.
Medidas de comprimento área, volume, massa e tempo.
Como vocês bem sabem, estou ministrando também as aulas de Estatística.
Aproveitem o período do curso para tirar TODAS as suas dúvidas no nosso
fórum.
Vamos em frente!
01. (RIOPREVIDENCIA 2010/CEPERJ) Na figura abaixo, os ângulos de
vértices B e C são retos, AB = 9m, BC = 11m e CD = 4m.
Então, entre as alternativas abaixo, a que mais se aproxima da distância entre
os pontos A e D é:
a)
b)
c)
d)
e)
15m
16m
17m
19m
21m
Resolução
Já que o objetivo é calcular a distância entre os pontos A e D, o primeiro passo
é traçar um segmento que ligue estes dois pontos.
1 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
4
11 E
9
4
Vamos também prolongar o segmento AB para a direita até o ponto E, de
forma que BE = CD.
Vamos ligar o ponto D ao ponto E. Obviamente
.
Está formado o triângulo retângulo ADE.
O cateto AE mede 13, o cateto DE mede 11 e queremos calcular a hipotenusa
AD.
Vamos aplicar o Teorema de Pitágoras que diz que o quadrado da hipotenusa
é igual à soma dos quadrados dos catetos.
O problema pede o valor mais próximo da medida de AD. Observe que
, portanto:
Letra C
02. (RIOPREVIDENCIA 2010/CEPERJ) Um cubo de ouro maciço com 2 cm de
aresta vale hoje R$ 9.120,00. O valor de um cubo de ouro maciço com 3 cm de
aresta é:
a)
b)
c)
d)
e)
R$ 13.680,00
R$ 18.240,00
R$ 20.250,00
R$ 27.360,00
R$ 30.780,00
Resolução
O valor de um cubo de ouro é proporcional à sua massa. Como o cubo é
maciço, podemos afirmar que o valor do cubo é proporcional ao seu volume (já
que a densidade do ouro é constante).
2 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
O volume de um cubo é igual ao cubo da medida da sua aresta.
A aresta do cubo que vale R$ 9.120,00 é igual a 2 cm. Logo, seu volume é
igual a:
Queremos calcular o valor de um cubo de aresta igual a 3 cm, cujo volume é
igual a:
Volume (cm3)
8
27
Preço (R$)
9.120
Quanto maior o volume do cubo, maior será o preço. As grandezas são
diretamente proporcionais.
Letra E
03. (METRO 2010/FCC) As medidas das arestas de um cubo são reduzidas a
1/3 de seu valor. Relativamente ao novo cubo obtido, é verdade que
(A) a sua área total é igual a 1/6 da área total do cubo original.
(B) o seu volume é igual a 1/9 do volume do cubo original.
(C) a sua área total é igual a 1/12 da área total do cubo original.
(D) o seu volume é igual a 1/27 do volume do cubo original.
(E) a área total é igual a 1/18 da área total do cubo original.
Resolução
Vamos considerar um cubo com arestas medindo . O seu volume é igual a:
Se as arestas são reduzidas a 1/3 de seu valor, então a nova aresta será igual
a 1/3 de x.
3 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
O novo volume será igual a:
Como
, então:
Letra D
04. (SEE-RJ 2010/CEPERJ) O terreno de uma grande fazenda é muito plano.
Certo dia, o fazendeiro saiu de casa com seu jipe e andou 11 km para o norte.
Em seguida, andou 6 km para o leste, 3 km para o sul e 2 km para oeste. Neste
ponto, a distância do fazendeiro à sua casa é de, aproximadamente:
a) 7 km
b) 8 km
c) 9 km
d) 10 km
e) 11 km
Resolução
O trajeto feito pelo fazendeiro é o seguinte:
Para calcular a distância do fazendeiro até sua casa, devemos ligar o ponto
inicial e o ponto final do trajeto. Podemos formar um triângulo retângulo como é
feito na figura abaixo.
4 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
Devemos aplicar o Teorema de Pitágoras no triângulo vermelho.
Como
, então:
Letra C
Observe a semelhança desta questão com a questão 1 desta aula!
05. (SEE-RJ 2010/CEPERJ) O triângulo retângulo ABC da figura abaixo tem
catetos AB = 8 e AC = 6. Pelo ponto M, médio da hipotenusa, traçou-se o
segmento MN perpendicular a BC. O segmento AN mede:
a) 7/4
b) 2
c) 9/4
d) 5/2
e) 11/4
Resolução
Vamos calcular o valor da hipotenusa do triângulo retângulo ABC.
5 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
Observe que os triângulos ABC e MNB são semelhantes: ambos são triângulos
retângulos e têm um ângulo em comum B. Vamos chamar o ângulo B de . O
outro ângulo agudo do triângulo ABC e o outro ângulo agudo do triângulo MNB
serão chamados de .
Como o ponto M é o ponto médio da hipotenusa BC, então
.
Os triângulos ABC e MNB são semelhantes.
â
â
â
â
Queremos calcular o comprimento do segmento AN. Percebe-se pela figura
que:
6 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
Letra A
06. (SEE-RJ 2007/CEPERJ) A figura abaixo mostra duas semicircunferências
de diâmetros AB e AC.
Se AB = 2 e BC = 1, a razão R/S entre as áreas das regiões R e S mostradas
na figura é:
A) 0,5
B) 0,6
C) 0,8
D) 1
E) 1,2
Resolução
Vamos calcular a área da região R que é uma semicircunferência.
Seu diâmetro AB mede 2, portanto seu raio mede 1. A área de uma
semicircunferência é a metade da área de uma circunferência.
Vamos calcular o raio da semicircunferência maior. Seu diâmetro é igual a:
Como o raio é a metade do diâmetro, então o raio da semicircunferência maior
é igual a 3/2.
A área da região S é igual à área da semicircunferência maior menos a área da
região R.
7 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
A razão R/S entre as áreas das regiões R e S mostradas na figura é:
Letra C
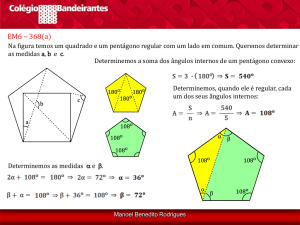
07. (Pref. de São Gonçalo 2007/CEPERJ) A figura abaixo mostra dois
pentágonos regulares colados.
O valor do ângulo ABC é:
A) 18o
B) 20o
C) 22o
D) 24o
E) 26o
Resolução
Para calcular a soma dos ângulos internos de um polígono com
utilizamos a fórmula:
lados
Desta forma, a soma dos ângulos internos de um pentágono é igual a:
8 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
Como os pentágonos do problema são regulares, então os pentágonos são
eqüiângulos (têm todos os ângulos com as mesmas medidas).
Para calcular a medida de cada ângulo dos pentágonos, devemos dividir
por .
Vamos calcular a medida do ângulo :
A soma dos ângulos internos de um triângulo é igual a 180º.
Como o triângulo ABC é isósceles, então os ângulos B e C são congruentes.
Vamos chamar os ângulos B e C de .
Letra A
9 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
08. (LIQUIGÁS 2008/CETRO) A figura abaixo é formada por um quadrado de
lado 6m “cortado” por um arco de circunferência.
Considerando =3,14, a área da região pintada de preto é
de
(A) 7,74m²
(B) 7,98m²
(C) 8,42m²
(D) 8,86m²
(E) 9,12m²
Resolução
A área de um quadrado de lado
circunferência de raio é igual a
.
é igual a
. A área de uma
Observe que a região branca é um quarto de círculo. Portanto, a área da
região pintada de preto é igual à área do quadrado menos a área branca.
Lembrando que a área branca é igual à área do círculo dividida por 4.
í
Letra A
09. (Agente de Trânsito – Pref. de Mairinque 2006/CETRO) Um pedreiro
construiu um muro ao redor de um terreno retangular que tinha um perímetro
de 96 metros. O comprimento desse terreno equivale ao triplo de sua largura.
As dimensões desse terreno valem
(A) 12 m por 36 m.
(B) 25 m por 50 m.
(C) 1 km por 12 km.
(D) 15 m por 32 m.
(E) 18 m por 36 m.
Resolução
Denotando a largura por x, o comprimento será 3x.
10 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
O perímetro é igual a 96m.
Assim,
Assim, a largura é 12m e o comprimento 3 x 12 = 36m.
Letra A
10. (Assistente Administrativo EBDA 2006/CETRO) Para construir um jardim,
um jardineiro recebeu as seguintes recomendações da dona da casa: o jardim
tem que ocupar uma área de 36m2, perímetro de 26m e formato retangular. As
dimensões desse jardim são de:
(A) 2m e 18m
(B) 20m e 6m
(C) 4m e 9m
(D) 3m e 12m
(E) 10m e 16m
Resolução
A área é o produto do comprimento da base pelo comprimento da altura.
Assim, temos que
Como o perímetro é igual a 26m, então
Dividindo ambos os membros por 2, temos
11 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
Devemos pensar em dois números cuja soma é 13 e o produto é 36. Podemos
testar as alternativas ou resolver o sistema. Rapidamente verificamos que a
alternativa C satisfaz as condições do problema.
Substituindo essa expressão na equação (I):
Assim,
Ou
.
Logo, as dimensões são 4m e 9m.
Letra C
11. (Assistente de Informática – Pref. de Itapeva 2006/CETRO) A soma das
áreas de dois quadrados é de 25 m2 e a soma dos seus perímetros é igual a
28m. Portanto, as medidas dos lados x e y desses quadrados são,
respectivamente:
Obs.:Figuras fora de escala.
12 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
(A) 3m e 4m
(B) 3,5m e 3,5m
(C) 5m e 2m
(D) 7m e 7m
(E) 20m e 8m
Resolução
A área de um quadrado é igual ao quadrado do seu lado.
Assim, um quadrado de lado tem área
.
A soma das áreas é igual a 25 m2. Podemos escrever que
Os quatro lados de um quadrado têm a mesma medida. Assim, o perímetro do
primeiro quadrado é 4x e o perímetro do segundo quadrado é 4y. Como a
soma dos perímetros é 28m, temos que
Dividindo ambos os membros por 4, temos
Neste ponto, podemos testar as alternativas e marcar a letra A.
Isolando o y:
Devemos agora substituir na primeira equação para encontrarmos os valores
das incógnitas:
Dividindo ambos os membros por 2,
13 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
Assim,
Ou
Assim, as dimensões são 3m e 4m.
Letra A
12. (Prefeitura Municipal de São José – FEPESE/2007) Tales de Mileto foi um
grande matemático grego que conseguia calcular a altura de pirâmides. O
famoso Teorema de Tales poderá ajudar você a encontrar as medidas
indicadas na figura, sendo que as retas r, s e t são paralelas e a distância entre
os pontos A e B é igual a 21.
Assinale a alternativa que represente o produto dos valores x e y.
a) 36.
b) 42.
c) 49.
d) 96.
e) 98.
Resolução
O Teorema de Tales diz que se duas retas são transversais de um feixe de
retas paralelas, então a razão entre dois segmentos quaisquer de uma
delas é igual à razão entre os respectivos segmentos correspondentes da
outra.
Observe que o segmento de comprimento 10 na reta da esquerda corresponde
ao segmento de comprimento y na reta da direita. O segmento de comprimento
14 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
30 (10+20) na reta da esquerda corresponde ao segmento AB de comprimento
21 (este valor encontra-se no enunciado). Assim,
Em toda proporção, o produto dos meios (30 e y) é igual ao produto dos
extremos (10 e 21).
Como o segmento AB mede 21 e y=7, então o segmento de comprimento 2x+2
mede 14.
O produto dos valores x e y é 6 x 7 = 42.
Letra B
13. (Agente Administrativo Municipal- Prefeitura Municipal de Pinheiral
2006/CETRO) Em um terreno plano, a sombra de um prédio, em determinada
hora do dia, mede 15m. Próximo ao prédio, e no mesmo instante, um poste de
5m. de altura, produz uma sombra que mede 3m. A altura do prédio, em
metros, é:
(A) 75
(B) 45
(C) 30
(D) 29
(E) 25
Resolução
15 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
Os dois triângulos acima são semelhantes, assim:
Letra E
14. (Prefeitura Municipal de Mairinque 2009/CETRO) Uma criança está ao lado
de um poste. Sabe-se que ela mede 80cm e que a medida da sombra do poste
é de 5,4 metros. Se a sombra da criança mede 60cm, então, a altura do poste
é de
(A) 6,2 metros.
(B) 6,6 metros.
(C) 6,8 metros.
(D) 7,0 metros.
(E) 7,2 metros.
Resolução
Os dois triângulos acima são semelhantes, assim:
16 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
Letra E
15. (ENAP 2006/ESAF) A razão de semelhança entre dois triângulos, T1, e T2,
é igual a 8. Sabe-se que a área do triângulo T1 é igual a 128 m2. Assim, a área
do triângulo T2 é igual a
a) 4 m2.
b) 16 m2.
c) 32 m2.
d) 64 m2.
e) 2 m2.
Resolução
Relembremos uma propriedade importantíssima:
A razão entre as áreas de duas superfícies semelhantes é igual ao quadrado
da razão de semelhança.
Assim,
Letra E
Essa propriedade é MUITO importante. Por exemplo, se triplicamos o raio
de um círculo (multiplicamos o raio por 3), então a área será multiplicada
por 32=9. Se a diagonal de um quadrado é quadruplicada (multiplicada por
4), então a área do quadrado é multiplicada por 42=16.
16. (Assistente Administrativo CRP 4ª 2006/CETRO) A distância entre dois
pontos é de 34 m. Num desenho, essa distância está expressa por 68 cm. A
escala usada para fazer esse desenho foi de:
(A) 1 : 50
(B) 1 : 40
(C) 1 : 30
17 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
(D) 1 : 20
(E) 1 : 10
Resolução
A escala em um mapa ou um desenho é a razão entre a medida do
desenho e a medida real (expressas na mesma unidade)
Letra A
17. (Assistente Administrativo EBDA 2006/CETRO) Um mapa está desenhado
na escala de 1 para 20.000. Qual o valor correto de uma distância indicada no
mapa por um segmento de reta de 9 cm?
(A) 180 metros
(B) 180 centímetros
(C) 18 quilômetros
(D) 1,8 quilômetros
(E) 18 centímetros
Resolução
Vimos na questão passada que
Letra D
18. (Prefeitura Municipal de São José – FEPESE/2007) Se dois ângulos são
suplementares e a medida do maior é 35º inferior ao quádruplo do menor,
assinale a alternativa que indica a medida do menor desses dois ângulos:
a) 25º
b) 36º
c) 43º
d) 65º
e) 137º
Resolução
18 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
Dois ângulos são suplementares se a soma de suas medidas é 180º. Em
tempo, dois ângulos são complementares se a soma de suas medidas é 90º e
dois ângulos são replementares se a soma de suas medidas é 360º.
Se um ângulo mede xº, o seu suplemento é denotado por sup
, o seu
complemento é denotado por
e o seu replemento é denotado por
Assim, tem-se as seguintes relações:
sup
comp
rep
Voltemos ao enunciado: Dois ângulos são suplementares. Digamos que o
maior meça x graus. Assim, o menor medirá (180 – x) graus.
A medida do maior é 35º inferior ao quádruplo do menor.
Atenção!!! A resposta não é a letra E!!! O problema pede o menor dos ângulos.
Como os ângulos são suplementares, o menor ângulo será
.
Letra C
19. (Agente de Trânsito – Pref. de Mairinque 2006/CETRO) Na figura abaixo,
as duas aberturas angulares apresentadas são suplementares. Qual o valor da
medida do ângulo X?
(A) 100º 45’
(B) 106º 37’
(C) 98º 99’
(D) 360º
(E) 111º 11’
Resolução
19 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
Vimos na questão passada que dois ângulos são suplementares se a soma de
suas medidas é 180º.
Se um ângulo mede xº, o seu suplemento é denotado por sup
e
sup
sup
Lembremos que 1º é o mesmo que 60’ (60 minutos). Assim, 180º = 179º60’ e
72º83’=73º23’
sup
Letra B
sup
20. (Prefeitura de Ituporanga 2009/FEPESE) Na figura abaixo, as retas r e s
são paralelas.
Se o ângulo a mede 44°30’ e o ângulo q mede 55°30’, então a medida do
ângulo b é:
a) 100°.
b) 55°30’.
c) 60°.
d) 44°30”.
e) 80°.
Resolução
Tracemos uma reta paralela às retas “r” e “s” pelo ponto de interseção dos
segmentos inclinados. O ângulo que fica acima da reta vermelha é igual a e o
ângulo que fica abaixo da reta vermelha é igual a . Isso é verdade pois
quando temos duas retas paralelas cortadas por uma transversal, os ângulos
alternos internos são congruentes.
20 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
Assim,
Letra A
21. (METRO 2010/FCC) Duas retas r e s, paralelas entre si, determinam com
e
uma reta transversal ângulos alternos internos expressos em graus por
. A medida de um desses ângulos é
(A) 48°.
(B) 40°.
(C) 35°.
(D) 28°.
(E) 25°.
Resolução
Ângulos alternos internos determinados por uma reta transversal à duas retas r
e s paralelas entre si sempre são congruentes.
Portanto:
21 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
Observe que esta não é a resposta da questão. O problema pede a medida dos
ângulos e não o valor de x.
Já que os ângulos são congruentes, podemos utilizar qualquer uma das
expressões acima.
Letra C
22. (Prefeitura de São José 2009/FEPESE) O menor ângulo que os ponteiros
das horas e dos minutos formam às 10 horas e 40 minutos é:
a) 60°
b) 40°
c) 20°
d) 75°
e) 80°
Resolução
Existe uma fórmula que não aparece nos livros de Geometria, mas que já foi
comentada na Revista do Professor de Matemática que fornece o menor
ângulo formado pelos ponteiros de um relógio. Denotando por H (horas) e M
(minutos), o ângulo (em graus) formado nos ponteiros do relógio é dado por
Letra E
23. (CGU 2003-2004/ESAF) Os ângulos de um triângulo encontram-se na
razão 2:3:4. O ângulo maior do triângulo, portanto, é igual a:
a) 40°
b) 70°
c) 75°
d) 80°
22 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
e) 90°
Resolução
Se os ângulos do triângulo encontram-se na razão 2:3:4, podemos chamá-los
de 2x, 3x e 4x. Lembremos da Lei Angular de Tales: a soma dos ângulos de
um triângulo qualquer é sempre 180º.
Assim,
O maior ângulo é
Letra D
24. (SUSEP 2010/ESAF) A soma S1 dos ângulos internos de um polígono
convexo de n lados, com n ≥ 3, é dada por Si=(n-2).1800. O número de lados
de três polígonos convexos, P1 , P2 , e P3, são representados, respectivamente,
por (x-3), x e (x+3). Sabendo-se que a soma de todos os ângulos internos dos
três polígonos é igual a 32400, então o número de lados do polígono P2 e o
total de diagonais do polígono P3 são, respectivamente, iguais a:
a) 5 e 5
b) 5 e 44
c) 11 e 44
d) 5 e 11
e) 11 e 5
Resolução
O enunciado foi muito generoso já fornecendo a fórmula da soma dos ângulos
internos de um polígono. O primeiro polígono tem (x – 3) lados. Assim, na
fórmula
devemos
substituir
o
“n”
por
“x
–
3”
obtendo
. O segundo polígono tem “x” lados, e, portanto, devemos
substituir o “n” por “x” obtendo
. Por fim, o terceiro polígono tem
(x+3) lados e a soma dos seus ângulos internos será
. Já que
a soma de todos os ângulos internos é 3240º, temos a seguinte equação:
23 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
Portanto, o número de lados de P2 é 8.
O primeiro polígono P1 possui 8 – 3 = 5 lados.
O polígono P3 possui 8+3 = 11 lados. O número de diagonais de um polígono
de n lados é dado por
Assim, o número de diagonais de P3 é
Questão anulada.
25. (AFT 2006/ESAF) Em um polígono de n lados, o número de diagonais
determinadas a partir de um de seus vértices é igual ao número de diagonais
de um hexágono. Desse modo, n é igual a:
a) 11
b) 12
c) 10
d) 15
e) 18
Resolução
Na questão passada mostrei a fórmula que fornece o número de diagonais de
um polígono convexo.
De cada vértice partem (n – 3) diagonais. Isso porque não podemos traçar
diagonais para o próprio vértice nem para os vértices adjacentes.
Um hexágono possui
Assim, se o polígono possui n lados, de cada vértice partem n – 3 diagonais.
Dessa forma,
24 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
Letra B
26. (Agente Administrativo Municipal- Prefeitura Municipal de Pinheiral
2006/CETRO) Um joalheiro recebe uma encomenda para uma jóia poligonal. O
comprador exige que o número de lados seja igual ao número de diagonais.
Sendo assim, o joalheiro deve produzir uma jóia
(A) triangular.
(B) quadrangular.
(C) pentagonal.
(D) hexagonal.
(E) decagonal.
Resolução
O número de diagonais é igual ao número de lados.
Como n > 0, podemos “cortar n em ambos os membros”.
Trata-se, portanto, de um pentágono. O pentágono possui 5 diagonais.
Letra C
25 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
27. (Analista de Sistemas – UDESC – FEPESE/2010) Seja ABCD o
paralelogramo abaixo, e seja E um ponto no segmento AD, conforme descrito
na figura abaixo:
Sabendo que AB = 5, AE = 3 e AD = 8, a área do paralelogramo
ABCD é:
a) 15.
b) 24.
c) 30.
d) 32.
e) 40.
Resolução
A área de um paralelogramo é o produto do comprimento da base pelo
comprimento da altura. O comprimento da base AD já foi fornecido: 8.
Precisamos calcular o comprimento da altura do paralelogramo. A altura é a
distância entre as bases: o segmento BE.
Para calcularmos o comprimento de BE, podemos aplicar o Teorema de
Pitágoras no triângulo ABE.
Os valores 5 e 3 foram fornecidos no enunciado. O Teorema de Pitágoras diz
que um triângulo é retângulo se e somente se a soma dos quadrados dos
catetos é igual ao quadrado da hipotenusa.
Assim,
26 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
Assim, a área do paralelogramo é dada por
Á
Letra D
28. (Pref. Municipal de Arujá 2006/CETRO) Em um trapézio, os lados paralelos
medem 16m e 44m, e os lados não paralelos, 17m e 25m. A área do trapézio,
em m2, é:
(A) 600.
(B) 550.
(C) 500.
(D) 450.
(E) 400
Resolução
Um quadrilátero plano convexo é um trapézio se e somente se possui dois
lados paralelos.
Lembremos a fórmula da área de um trapézio:
Onde B é a base maior, b é a base menor e h é a altura. Para calcularmos a
altura, devemos projetar a base menor sobre a base maior.
27 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
A base maior ficou dividida em três segmentos. O da esquerda foi chamado de
x. O do meio é igual à base menor: 16. Já que a base maior mede 44, então o
segmento da esquerda mede 44 – x – 16 = 28 – x.
Apliquemos o Teorema de Pitágoras no triângulo retângulo da esquerda:
Apliquemos o Teorema de Pitágoras no triângulo retângulo da direita:
Sabemos por (I) que
Assim,
Voltemos para (I).
A fórmula da área de um trapézio:
Letra D
28 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
29. (Agente Administrativo Municipal- Prefeitura Municipal de Pinheiral
2006/CETRO) Durante um vendaval, um poste de iluminação de 18 metros de
altura quebrou-se em um ponto a certa altura do solo. A parte do poste acima
da fratura, inclinou-se, e sua extremidade superior encostou no solo a uma
distância de 12 metros da base dele. Calcule a quantos metros de altura do
solo quebrou-se o poste.
(A) 6
(B) 5
(C) 4
(D) 3
(E) 2
Resolução
O poste quebrado está mais espesso no desenho. Se o segmento vertical
mede x metros, então o segmento inclinado medirá 18 – x, já que a soma dos
dois segmentos deve ser 18 m (altura do poste).
Apliquemos o Teorema de Pitágoras no triângulo retângulo.
Letra B
30. (SUSEP 2010/ESAF) Um círculo está inscrito em um triângulo isósceles de
base 6 e altura 4. Calcule o raio desse círculo.
a) 1,50
b) 1,25
c) 1,00
d) 1,75
29 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
e) 2,00
Resolução
Pelo Teorema de Pitágoras, os lados congruentes do triângulo isósceles
medem 5.
Pois, se os lados congruentes medem x, então
A área do triângulo é igual à metade do produto da base pela altura.
Assim,
A área do triângulo pode ser expressa como o produto do semiperímetro (p)
pelo raio da circunferência inscrita ao triângulo.
Assim,
Letra A
31. (Secretaria de Administração – Balneário Camboriú – FEPESE/2007) Um
terreno tem a forma triangular, e seus lados medem 40 m, 90 m e 110 m. A
área desse terreno, em metros quadrados, é:
a) 1800
b) 2200
30 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
c) 1950
d) 1200
e) 240
Resolução
Existem diversas formas para calcular a área de um triângulo, a depender dos
dados fornecidos. Já vimos duas: i) A metade do produto da base pela altura. ii)
Produto do semiperímetro pelo raio da circunferência inscrita. Vejamos outra
maneira: quando forem dados os três lados, calculamos a área utilizando a
fórmula de Heron. Denotemos por “p” o semiperímetro. A área é dada por:
O semiperímetro é a semi-soma dos lados.
A área é igual a
Letra D
32. (Prefeitura de Ituporanga 2009/FEPESE) Se em um triângulo os lados
medem 12 cm, 16 cm e 20 cm, então a altura relativa ao maior lado mede:
a) 10,3 cm.
b) 6,0 cm.
c) 7,2 cm.
d) 5,6 cm.
e) 9,6 cm.
Resolução
Sabemos que quando são dados os três lados de um triângulo, podemos
calcular a área pela fórmula de Heron. Sabemos também que a área é a
31 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
metade do produto da base pela altura (qualquer lado pode ser a base, e
utilizamos a altura relativa a esse lado).
O semiperímetro é dado por
A área é igual a
Como 24 = 12 x 2,
E 2 x 8 = 16,
A área é igual a 96 e pode ser calculada como a metade do produto da base
pela altura. Como queremos calcular a altura relativa ao maior lado, tomaremos
o lado de comprimento 20 como base.
Letra E
33. (ENAP 2006/ESAF) A base de um triângulo isósceles é 2 metros menor do
que a altura relativa à base. Sabendo-se que o perímetro deste triângulo é igual
a 36 metros, então a altura e a base medem, respectivamente
a) 8 m e 10 m.
b) 12 m e 10 m.
c) 6 m e 8 m.
d) 14 m e 12 m.
e) 16 m e 14 m.
32 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
Resolução
Todo triângulo isósceles possui dois lados congruentes. O lado não-congruente
é chamado de base. A altura relativa à base divide-a em dois segmentos de
mesmo comprimento: chamemo-los de x. Assim, a base mede 2x. Como a
base de um triângulo isósceles é 2 metros menor do que a altura relativa à
base, então essa altura mede 2x+2. Chamarei os lados congruentes de y.
O enunciado nos informou que o perímetro do triângulo é igual a 36. Assim,
Dividindo ambos os membros por 2, temos
Ao traçarmos a altura relativa a base, obtemos dois triângulos retângulos que
podemos aplicar o Teorema de Pitágoras.
Como
Dividindo ambos os membros por 4, obtemos:
33 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
Como x > 0, então
A base é 2x, logo a base é
Como a altura é 2x+2, então
Letra B
34. (TRT-SC 2005/FEPESE) Um círculo de área 16 está inscrito em um
quadrado. O perímetro do quadrado é igual a:
a) 32
b) 28
c) 24
d) 20
e) 16
Resolução
A área de um círculo de raio r é igual a
Como a área é igual a
.
, então
O círculo está inscrito em um quadrado.
34 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
Observe que o lado do quadrado é igual ao dobro do raio do círculo (diâmetro).
Assim,
O perímetro do quadrado é igual a
Letra A
35. (Prefeitura de Ituporanga 2009/FEPESE) Na circunferência abaixo:
Determine a medida x indicada.
a) 3
b) 6
c) 7
d) 10
e) 12
Resolução
Vamos relembrar a relação entre cordas que existe em uma circunferência e a
relação que existe entre os segmentos que cortam uma circunferência a partir
de um ponto exterior.
35 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
“Se duas cordas de uma mesma circunferência se interceptam, então o produto
das medidas das duas partes de uma é igual ao produto das medidas das duas
partes da outra”.
Em suma,
.
“Se por um ponto (P) exterior a uma circunferência conduzimos dois
“segmentos secantes” (PB e PD), então o produto da medida do primeiro (PB)
pela de sua parte exterior (PA) é igual ao produto do segundo (PD) pela de sua
parte exterior (PD).”
Em suma,
.
Voltemos ao problema.
Pela teoria exposta,
36 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
Letra D
36. (BADESC 2010/FGV) Uma circunferência de centro em O está inscrita em
um quadrado de vértices A, B, C e D, como ilustrado. P, Q e R são pontos em
que a circunferência toca o quadrado.
Com relação à figura, analise as afirmativas a seguir:
I. A área interior ao quadrado e exterior à circunferência é menor do que a
metade da área total do quadrado.
II. A distância de A até O é menor do que a metade da medida do lado do
quadrado.
III. O percurso PRQ, quando feito por cima da circunferência, é mais curto do
que o feito por sobre os lados do quadrado. Assinale:
(A) se somente a afirmativa I estiver correta.
(B) se somente a afirmativa II estiver correta.
(C) se somente a afirmativa III estiver correta.
(D) se somente as afirmativas I e III estiverem corretas.
(E) se somente as afirmativas II e III estiverem corretas.
Resolução
Se o raio da circunferência for igual a , então o lado do quadrado é igual a
Comprimento da circunferência:
Área do círculo:
r
Área do quadrado:
Vamos analisar cada uma das alternativas de per si.
37 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
I. A área interior ao quadrado e exterior à circunferência é menor do que a
metade da área total do quadrado.
Para calcular a área interior ao quadrado e exterior à circunferência, devemos
calcular a diferença entre a área do quadrado e a área do círculo.
ã
ã
Usando uma boa aproximação para o número
Como á área do quadrado é
ã
:
, então a metade da área do quadrado é
Portanto, a área interior ao quadrado e exterior à circunferência é menor do
que a metade da área total do quadrado.
O item é verdadeiro.
II. A distância de A até O é menor do que a metade da medida do lado do
quadrado.
O triângulo em destaque na figura é retângulo de catetos iguais a . A distância
AO pode ser calculada pelo Teorema de Pitágoras:
38 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
Portanto, a distância de A até O é maior do que a metade da medida do lado
do quadrado. Isto porque a metade da medida do lado do quadrado é igual ao
.
raio da circunferência e
O item é falso.
III. O percurso PRQ, quando feito por cima da circunferência, é mais curto do
que o feito por sobre os lados do quadrado.
O percurso PQR feito por cima da circunferência equivale a 3/4 do
comprimento da circunferência.
O mesmo percurso feito pelos lados do quadrado:
Este comprimento é igual a
.
39 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
Como
o percurso PRQ, quando feito por cima da circunferência, é
mais curto do que o feito por sobre os lados do quadrado. O item é verdadeiro.
Letra D
40 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
Relação das questões comentadas nesta aula
01. (RIOPREVIDENCIA 2010/CEPERJ) Na figura abaixo, os ângulos de
vértices B e C são retos, AB = 9m, BC = 11m e CD = 4m.
Então, entre as alternativas abaixo, a que mais se aproxima da distância entre
os pontos A e D é:
a)
b)
c)
d)
e)
15m
16m
17m
19m
21m
02. (RIOPREVIDENCIA 2010/CEPERJ) Um cubo de ouro maciço com 2 cm de
aresta vale hoje R$ 9.120,00. O valor de um cubo de ouro maciço com 3 cm de
aresta é:
a)
b)
c)
d)
e)
R$ 13.680,00
R$ 18.240,00
R$ 20.250,00
R$ 27.360,00
R$ 30.780,00
03. (METRO 2010/FCC) As medidas das arestas de um cubo são reduzidas a
1/3 de seu valor. Relativamente ao novo cubo obtido, é verdade que
(A) a sua área total é igual a 1/6 da área total do cubo original.
(B) o seu volume é igual a 1/9 do volume do cubo original.
(C) a sua área total é igual a 1/12 da área total do cubo original.
(D) o seu volume é igual a 1/27 do volume do cubo original.
(E) a área total é igual a 1/18 da área total do cubo original.
04. (SEE-RJ 2010/CEPERJ) O terreno de uma grande fazenda é muito plano.
Certo dia, o fazendeiro saiu de casa com seu jipe e andou 11 km para o norte.
Em seguida, andou 6 km para o leste, 3 km para o sul e 2 km para oeste. Neste
ponto, a distância do fazendeiro à sua casa é de, aproximadamente:
a) 7 km
b) 8 km
41 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
c) 9 km
d) 10 km
e) 11 km
05. (SEE-RJ 2010/CEPERJ) O triângulo retângulo ABC da figura abaixo tem
catetos AB = 8 e AC = 6. Pelo ponto M, médio da hipotenusa, traçou-se o
segmento MN perpendicular a BC. O segmento AN mede:
a) 7/4
b) 2
c) 9/4
d) 5/2
e) 11/4
06. (SEE-RJ 2007/CEPERJ) A figura abaixo mostra duas semicircunferências
de diâmetros AB e AC.
Se AB = 2 e BC = 1, a razão R/S entre as áreas das regiões R e S mostradas
na figura é:
A) 0,5
B) 0,6
C) 0,8
D) 1
E) 1,2
42 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
07. (Pref. de São Gonçalo 2007/CEPERJ) A figura abaixo mostra dois
pentágonos regulares colados.
O valor do ângulo ABC é:
A) 18o
B) 20o
C) 22o
D) 24o
E) 26o
08. (LIQUIGÁS 2008/CETRO) A figura abaixo é formada por um quadrado de
lado 6m “cortado” por um arco de circunferência.
Considerando =3,14, a área da região pintada de preto é
de
(A) 7,74m²
(B) 7,98m²
(C) 8,42m²
(D) 8,86m²
(E) 9,12m²
09. (Agente de Trânsito – Pref. de Mairinque 2006/CETRO) Um pedreiro
construiu um muro ao redor de um terreno retangular que tinha um perímetro
de 96 metros. O comprimento desse terreno equivale ao triplo de sua largura.
As dimensões desse terreno valem
(A) 12 m por 36 m.
(B) 25 m por 50 m.
(C) 1 km por 12 km.
(D) 15 m por 32 m.
(E) 18 m por 36 m.
43 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
10. (Assistente Administrativo EBDA 2006/CETRO) Para construir um jardim,
um jardineiro recebeu as seguintes recomendações da dona da casa: o jardim
tem que ocupar uma área de 36m2, perímetro de 26m e formato retangular. As
dimensões desse jardim são de:
(A) 2m e 18m
(B) 20m e 6m
(C) 4m e 9m
(D) 3m e 12m
(E) 10m e 16m
11. (Assistente de Informática – Pref. de Itapeva 2006/CETRO) A soma das
áreas de dois quadrados é de 25 m2 e a soma dos seus perímetros é igual a
28m. Portanto, as medidas dos lados x e y desses quadrados são,
respectivamente:
Obs.:Figuras fora de escala.
(A) 3m e 4m
(B) 3,5m e 3,5m
(C) 5m e 2m
(D) 7m e 7m
(E) 20m e 8m
12. (Prefeitura Municipal de São José – FEPESE/2007) Tales de Mileto foi um
grande matemático grego que conseguia calcular a altura de pirâmides. O
famoso Teorema de Tales poderá ajudar você a encontrar as medidas
indicadas na figura, sendo que as retas r, s e t são paralelas e a distância entre
os pontos A e B é igual a 21.
Assinale a alternativa que represente o produto dos valores x e y.
44 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
a) 36.
b) 42.
c) 49.
d) 96.
e) 98.
13. (Agente Administrativo Municipal- Prefeitura Municipal de Pinheiral
2006/CETRO) Em um terreno plano, a sombra de um prédio, em determinada
hora do dia, mede 15m. Próximo ao prédio, e no mesmo instante, um poste de
5m. de altura, produz uma sombra que mede 3m. A altura do prédio, em
metros, é:
(A) 75
(B) 45
(C) 30
(D) 29
(E) 25
14. (Prefeitura Municipal de Mairinque 2009/CETRO) Uma criança está ao lado
de um poste. Sabe-se que ela mede 80cm e que a medida da sombra do poste
é de 5,4 metros. Se a sombra da criança mede 60cm, então, a altura do poste
é de
(A) 6,2 metros.
(B) 6,6 metros.
(C) 6,8 metros.
(D) 7,0 metros.
(E) 7,2 metros.
15. (ENAP 2006/ESAF) A razão de semelhança entre dois triângulos, T1, e T2,
é igual a 8. Sabe-se que a área do triângulo T1 é igual a 128 m2. Assim, a área
do triângulo T2 é igual a
a) 4 m2.
b) 16 m2.
c) 32 m2.
d) 64 m2.
e) 2 m2.
16. (Assistente Administrativo CRP 4ª 2006/CETRO) A distância entre dois
pontos é de 34 m. Num desenho, essa distância está expressa por 68 cm. A
escala usada para fazer esse desenho foi de:
(A) 1 : 50
(B) 1 : 40
(C) 1 : 30
(D) 1 : 20
(E) 1 : 10
17. (Assistente Administrativo EBDA 2006/CETRO) Um mapa está desenhado
na escala de 1 para 20.000. Qual o valor correto de uma distância indicada no
mapa por um segmento de reta de 9 cm?
(A) 180 metros
(B) 180 centímetros
45 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
(C) 18 quilômetros
(D) 1,8 quilômetros
(E) 18 centímetros
18. (Prefeitura Municipal de São José – FEPESE/2007) Se dois ângulos são
suplementares e a medida do maior é 35º inferior ao quádruplo do menor,
assinale a alternativa que indica a medida do menor desses dois ângulos:
a) 25º
b) 36º
c) 43º
d) 65º
e) 137º
19. (Agente de Trânsito – Pref. de Mairinque 2006/CETRO) Na figura abaixo,
as duas aberturas angulares apresentadas são suplementares. Qual o valor da
medida do ângulo X?
(A) 100º 45’
(B) 106º 37’
(C) 98º 99’
(D) 360º
(E) 111º 11’
20. (Prefeitura de Ituporanga 2009/FEPESE) Na figura abaixo, as retas r e s
são paralelas.
Se o ângulo a mede 44°30’ e o ângulo q mede 55°30’, então a medida do
ângulo b é:
a) 100°.
b) 55°30’.
c) 60°.
d) 44°30”.
e) 80°.
46 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
21. (METRO 2010/FCC) Duas retas r e s, paralelas entre si, determinam com
e
uma reta transversal ângulos alternos internos expressos em graus por
. A medida de um desses ângulos é
(A) 48°.
(B) 40°.
(C) 35°.
(D) 28°.
(E) 25°.
22. (Prefeitura de São José 2009/FEPESE) O menor ângulo que os ponteiros
das horas e dos minutos formam às 10 horas e 40 minutos é:
a) 60°
b) 40°
c) 20°
d) 75°
e) 80°
23. (CGU 2003-2004/ESAF) Os ângulos de um triângulo encontram-se na
razão 2:3:4. O ângulo maior do triângulo, portanto, é igual a:
a) 40°
b) 70°
c) 75°
d) 80°
e) 90°
24. (SUSEP 2010/ESAF) A soma S1 dos ângulos internos de um polígono
convexo de n lados, com n ≥ 3, é dada por Si=(n-2).1800. O número de lados
de três polígonos convexos, P1 , P2 , e P3, são representados, respectivamente,
por (x-3), x e (x+3). Sabendo-se que a soma de todos os ângulos internos dos
três polígonos é igual a 32400, então o número de lados do polígono P2 e o
total de diagonais do polígono P3 são, respectivamente, iguais a:
a) 5 e 5
b) 5 e 44
c) 11 e 44
d) 5 e 11
e) 11 e 5
25. (AFT 2006/ESAF) Em um polígono de n lados, o número de diagonais
determinadas a partir de um de seus vértices é igual ao número de diagonais
de um hexágono. Desse modo, n é igual a:
a) 11
b) 12
c) 10
d) 15
e) 18
47 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
26. (Agente Administrativo Municipal- Prefeitura Municipal de Pinheiral
2006/CETRO) Um joalheiro recebe uma encomenda para uma jóia poligonal. O
comprador exige que o número de lados seja igual ao número de diagonais.
Sendo assim, o joalheiro deve produzir uma jóia
(A) triangular.
(B) quadrangular.
(C) pentagonal.
(D) hexagonal.
(E) decagonal.
27. (Analista de Sistemas – UDESC – FEPESE/2010) Seja ABCD o
paralelogramo abaixo, e seja E um ponto no segmento AD, conforme descrito
na figura abaixo:
Sabendo que AB = 5, AE = 3 e AD = 8, a área do paralelogramo
ABCD é:
a) 15.
b) 24.
c) 30.
d) 32.
e) 40.
28. (Pref. Municipal de Arujá 2006/CETRO) Em um trapézio, os lados paralelos
medem 16m e 44m, e os lados não paralelos, 17m e 25m. A área do trapézio,
em m2, é:
(A) 600.
(B) 550.
(C) 500.
(D) 450.
(E) 400
29. (Agente Administrativo Municipal- Prefeitura Municipal de Pinheiral
2006/CETRO) Durante um vendaval, um poste de iluminação de 18 metros de
altura quebrou-se em um ponto a certa altura do solo. A parte do poste acima
da fratura, inclinou-se, e sua extremidade superior encostou no solo a uma
distância de 12 metros da base dele. Calcule a quantos metros de altura do
solo quebrou-se o poste.
(A) 6
(B) 5
(C) 4
(D) 3
(E) 2
48 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
30. (SUSEP 2010/ESAF) Um círculo está inscrito em um triângulo isósceles de
base 6 e altura 4. Calcule o raio desse círculo.
a) 1,50
b) 1,25
c) 1,00
d) 1,75
e) 2,00
31. (Secretaria de Administração – Balneário Camboriú – FEPESE/2007) Um
terreno tem a forma triangular, e seus lados medem 40 m, 90 m e 110 m. A
área desse terreno, em metros quadrados, é:
a) 1800
b) 2200
c) 1950
d) 1200
e) 240
32. (Prefeitura de Ituporanga 2009/FEPESE) Se em um triângulo os lados
medem 12 cm, 16 cm e 20 cm, então a altura relativa ao maior lado mede:
a) 10,3 cm.
b) 6,0 cm.
c) 7,2 cm.
d) 5,6 cm.
e) 9,6 cm.
33. (ENAP 2006/ESAF) A base de um triângulo isósceles é 2 metros menor do
que a altura relativa à base. Sabendo-se que o perímetro deste triângulo é igual
a 36 metros, então a altura e a base medem, respectivamente
a) 8 m e 10 m.
b) 12 m e 10 m.
c) 6 m e 8 m.
d) 14 m e 12 m.
e) 16 m e 14 m.
34. (TRT-SC 2005/FEPESE) Um círculo de área 16 está inscrito em um
quadrado. O perímetro do quadrado é igual a:
a) 32
b) 28
c) 24
d) 20
e) 16
49 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
35. (Prefeitura de Ituporanga 2009/FEPESE) Na circunferência abaixo:
Determine a medida x indicada.
a) 3
b) 6
c) 7
d) 10
e) 12
36. (BADESC 2010/FGV) Uma circunferência de centro em O está inscrita em
um quadrado de vértices A, B, C e D, como ilustrado. P, Q e R são pontos em
que a circunferência toca o quadrado.
Com relação à figura, analise as afirmativas a seguir:
I. A área interior ao quadrado e exterior à circunferência é menor do que a
metade da área total do quadrado.
II. A distância de A até O é menor do que a metade da medida do lado do
quadrado.
III. O percurso PRQ, quando feito por cima da circunferência, é mais curto do
que o feito por sobre os lados do quadrado. Assinale:
50 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
(A) se somente a afirmativa I estiver correta.
(B) se somente a afirmativa II estiver correta.
(C) se somente a afirmativa III estiver correta.
(D) se somente as afirmativas I e III estiverem corretas.
(E) se somente as afirmativas II e III estiverem corretas.
51 www.pontodosconcursos.com.br
CURSO ON-LINE – PACOTE DE EXERCÍCIOS – SEPLAG/RJ
Gabaritos
01. C
02. E
03. D
04. C
05. A
06. C
07. A
08. A
09. A
10. C
11. A
12. B
13. E
14. E
15. E
16. A
17. D
18. C
19. B
20. A
21. C
22. E
23. D
24. ANULADA
25. B
26. C
27. D
28. D
29. B
30. A
31. D
32. E
33. B
34. A
35. D
36. D
52 www.pontodosconcursos.com.br