Vestibular UFPR 2014/2015 1ª fase

Calculândia – Escola de Reforço para Ensino Médio e Fundamental
Exercícios Resolvidos – FÍSICA ­ UFPR 2014/2015 – 1ª fase
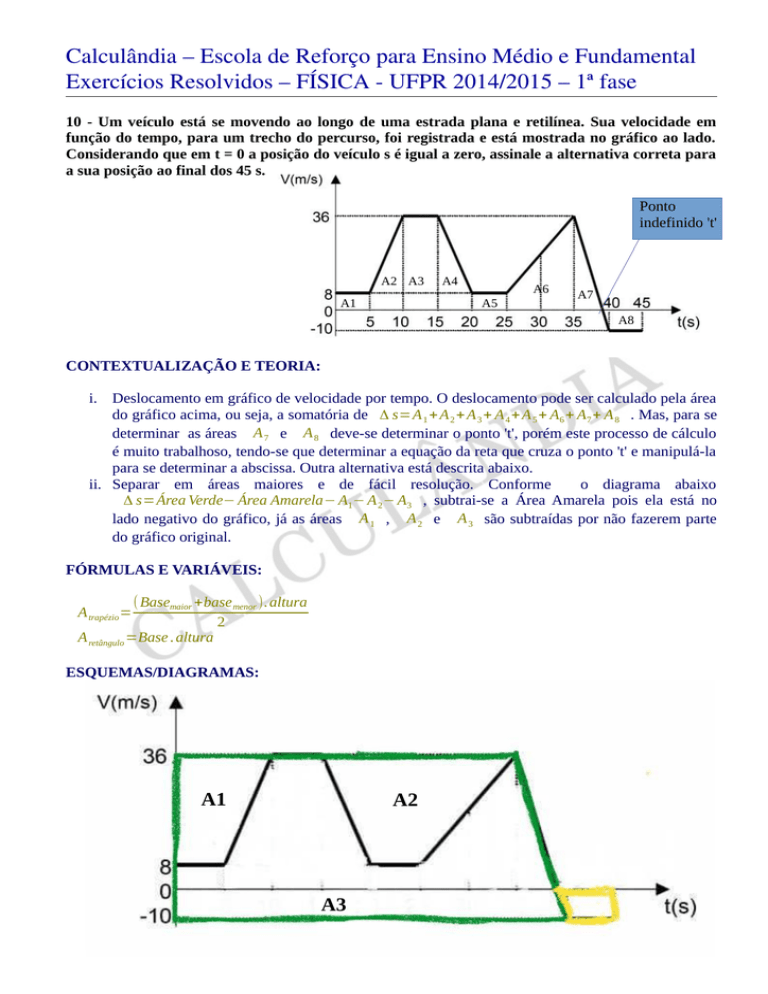
10 - Um veículo está se movendo ao longo de uma estrada plana e retilínea. Sua velocidade em
função do tempo, para um trecho do percurso, foi registrada e está mostrada no gráfico ao lado.
Considerando que em t = 0 a posição do veículo s é igual a zero, assinale a alternativa correta para
a sua posição ao final dos 45 s.
Ponto
indefinido 't'
A2 A3
A1
A4
A6
A5
A7
A8
CONTEXTUALIZAÇÃO E TEORIA:
i. Deslocamento em gráfico de velocidade por tempo. O deslocamento pode ser calculado pela área
do gráfico acima, ou seja, a somatória de Δ s=A 1 + A 2 + A 3 + A 4 + A 5 + A6 + A7 + A 8 . Mas, para se
determinar as áreas A 7 e A 8 deve-se determinar o ponto 't', porém este processo de cálculo
é muito trabalhoso, tendo-se que determinar a equação da reta que cruza o ponto 't' e manipulá-la
para se determinar a abscissa. Outra alternativa está descrita abaixo.
ii. Separar em áreas maiores e de fácil resolução. Conforme
o diagrama abaixo
Δ s=Área Verde− Área Amarela− A1− A 2− A3 , subtrai-se a Área Amarela pois ela está no
lado negativo do gráfico, já as áreas A 1 , A 2 e A 3 são subtraídas por não fazerem parte
do gráfico original.
FÓRMULAS E VARIÁVEIS:
( Basemaior +base menor ). altura
2
A retângulo =Base . altura
A trapézio =
ESQUEMAS/DIAGRAMAS:
A1
A2
A3
Calculândia – Escola de Reforço para Ensino Médio e Fundamental
Exercícios Resolvidos – FÍSICA ­ UFPR 2014/2015 – 1ª fase
RESOLUÇÃO:
Sabemos que:
Δ s=Área Verde− Área Amarela− A1− A 2− A3 , ou:
Δ s=Área Verde−(Área Amarela + A3 )− A 1−A 2
(40+35).(36+10)
=1725 m
2
Área Amarela + A3 =A retângulo=45.10=450 m
(10+5).(36−8)
A 1= A trapézio=
=210 m
2
((35−15)+(25−20)).(36−8)
A 2= A trapézio =
=350 m
2
Área Verde= A trapézio =
logo:
Δ s=1725 m−450 m−210 m−350 m=715 m
Δ s=715 m
11 - Um objeto de massa m está em movimento circular, deslizando sobre um plano inclinado. O
objeto está preso em uma das extremidades de uma corda de comprimento L, cuja massa e
elasticidade são desprezíveis. A outra extremidade da corda está fixada na superfície de um plano
inclinado, conforme indicado na figura a seguir. O plano inclinado faz um ângulo θ=30° em
1
relação ao plano horizontal. Considerando g a aceleração da gravidade e μ=
o coeficiente
π √3
de atrito cinético entre a superfície do plano inclinado e o objeto, assinale a alternativa correta
para a variação da energia cinética do objeto, em módulo, ao se mover do ponto P, cuja velocidade
em módulo é v p , ao ponto Q, onde sua velocidade tem módulo v q . Na resolução desse
1
√3 .
problema considere sen 30°=
cos30 °=
2
2
CONTEXTUALIZAÇÃO E TEORIA:
i. Teoria da conservação de energia. Neste caso deve-se considerar o atrito do objeto com o plano
inclinado, sendo, portanto, um sistema não conservativo. Logo a variação da energia mecânica (
Δ E ) será igual à energia dissipada pelas forças não-conservativas ( W nc ). Neste problema a
única força não-conservativa citada é a força de atrito.
ii. Planos inclinados. Para que se possa calcular a energia dissipada, deve-se conhecer a força de
atrito existente, para isso, a força Normal do objeto em relação ao plano de apoio deve ser
calculada através dos conhecimentos de planos inclinados e decomposição de vetores da força
peso.
iii. Trabalho da força de atrito. A energia dissipada do sistema é equivalente ao trabalho das forças
não-conservativas ( W nc ), no caso o trabalho da força de atrito. Lembrando que trabalho é o
produto escalar da força pelo deslocamento.
Calculândia – Escola de Reforço para Ensino Médio e Fundamental
Exercícios Resolvidos – FÍSICA ­ UFPR 2014/2015 – 1ª fase
FÓRMULAS E VARIÁVEIS:
Δ E=Δ K + ΔU
Δ U =U final−U inicial
U=m. g . h
W nc =Δ E
W nc =τ atrito =μ . N . Δ x . cos α
ESQUEMAS/DIAGRAMAS:
RESOLUÇÃO:
A resposta é a variação de energia cinética, Δ K =?
A principal forma de relacionarmos energia cinética, energia potencial, atrito e outras energias não
conservativas, é através do Teorema da Conservação do Trabalho e Energia.
W nc =Δ E
Em que W nc =trabalho de forças não conservativas , neste problema apenas o atrito é citado como
Δ E=variação da energia mecânica do sistema=Δ K +Δ U (todas as
força não conservativa, e
energias conservativas do sistemas)logo:
W nc =trabalho da força de atrito= τatrito =μ . N . Δ x . cos α , em que N=força normal
α=ângulo entre o vetor força e o vetor deslocamento , no caso da força de atrito α=180 °
Logo,
μ . N . Δ x .cos 180°=Δ K +ΔU ,
em que Δ K =variação da energia cinética e Δ U =variação da energia potencial , logo,
μ . N . Δ x .cos 180° =Δ K +U final−U inicial ;
μ . N . Δ x .cos 180° =Δ K +m . g . hq −m. g . h p ,
Calculândia – Escola de Reforço para Ensino Médio e Fundamental
Exercícios Resolvidos – FÍSICA ­ UFPR 2014/2015 – 1ª fase
sabemos que:
h p=0 ;
1 hq
logo hq =L ;
=
2 2L
2. π. raio
Δ x=trajetória do objeto=semicircunferência=
=π. raio=π . L
2
sen 30°=
h
cateto oposto
= q ,
hipotenusa
L+ L
Lembrado da teoria de plano inclinado:
cos 30 °=
cateto adjacente N
, em que P=força peso=m . g logo:
=
hipotenusa
P
√3
N=m. g . cos 30 °=m . g .
2
Substituindo tudo em μ . N . Δ x .cos 180° =Δ K +m . g . hq −m. g . h p , temos:
1
3
(
).(m . g . √ ).(π. L).(−1)=Δ K +m . g . L−m. g .0
2
π . √3
−m . g . L
−3. m. g . L
, em módulo:
−m. g . L=Δ K , Δ K =
2
2
3
|Δ K|= . m. g . L
2
12- Um bloco B de massa 400 g está apoiado sobre um bloco A de massa 800 g, o qual está sobre
uma superfície horizontal. Os dois blocos estão unidos por uma corda inextensível e sem massa,
que passa por uma polia presa na parede, conforme ilustra a figura ao lado. O coeficiente de atrito
cinético entre os dois blocos e entre o bloco A e a superfície horizontal é o mesmo e vale 0,35.
Considerando a aceleração da gravidade igual a 10 m/s 2 e desprezando a massa da polia, assinale
a alternativa correta para o módulo da força F necessária para que os dois blocos se movam com
velocidade constante.
CONTEXTUALIZAÇÃO E TEORIA:
i. Velocidade constante. Neste caso a aceleração é nula, portanto a força resultante de cada corpo é
F =m. ⃗a =⃗
0 ).
nula ( ⃗
ii. Diagrama de forças atuantes. Para facilitar o cálculo, separa-se o sistema em dois diagramas, um
para o corpo A com a forças atuantes sobre o corpo e outro pra o corpo B com a forças que atuam
sobe ele, conforme desenhado abaixo.
iii. Força de atrito. Lembre que a força de atrito é sempre contrária ao sentido do movimento e
proporcional à força normal. Para o corpo B, a normal é a reação ao peso de B, já para o corpo A,
a normal é a reação do peso de A e B, já que ambos pressionam A contra o solo.
Calculândia – Escola de Reforço para Ensino Médio e Fundamental
Exercícios Resolvidos – FÍSICA ­ UFPR 2014/2015 – 1ª fase
FÓRMULAS E VARIÁVEIS:
⃗
F =m. ⃗a
⃗
F atrito=μ . ⃗
N
ESQUEMAS/DIAGRAMAS:
RESOLUÇÃO:
Diagrama do corpo A:
T + F aAB + F aAS −F=0 (I)
Diagrama do corpo B:
T −F aAB=0 , ou seja,
T =F aAB (II)
Substituindo a equação (II) em (I), tem-se:
F aAB +F aAB + F aAS −F=0
F aAB +F aAB + F aAS −F=0
2. F aAB + F aAS−F=0
Sendo:
F aAB=μ . N AB =μ . g . mB
F aAS =μ . N AS =μ . g .(m A +m B)
Logo:
2.μ . g .m B +μ . g .(m A + mB)−F=0 ,
2.0,35 .10 m/s ².0,4 kg+0,35 .10 m/s ².(0,8 kg+ 0,4 kg)−F=0
F=7,0 N
Calculândia – Escola de Reforço para Ensino Médio e Fundamental
Exercícios Resolvidos – FÍSICA ­ UFPR 2014/2015 – 1ª fase
13 - O estudo da calorimetria e das leis da termodinâmica nos dá explicações para vários
fenômenos encontrados na natureza. Considere o seguinte texto que apresenta a explicação, do
ponto de vista dessas áreas da Física, para a formação das nuvens: Quando uma porção de ar
aquecido sobe, contendo água que acabou de __________ da superfície, passa a estar submetida a
uma pressão cada vez __________. A rápida variação na pressão provoca uma rápida expansão do
ar junto com uma redução de seu/sua __________. Essa rápida expansão é considerada
__________, isto é, sem troca de calor com sua vizinhança, porque ocorre muito rapidamente. O
gás em expansão __________ energia interna ao se expandir, e isso acarreta seu resfriamento até
atingir uma temperatura na qual a quantidade de vapor de água é suficiente para saturar o ar
naquele ponto e assim formar as nuvens. Assinale a alternativa que preenche as lacunas
corretamente.
RESOLUÇÃO:
Evaporar: A água retorna para a atmosfera através da evaporação, transformação do estado líquido para
o gasoso.
Menor: Conforme se distancia do nível do mar, a pressão atmosférica diminui, pois o ar é mais rarefeito.
Característica comprovada pelo experimento de Torricelli.
Temperatura: A expansão do gás exige trabalho, como a expansão é muito rápida, não há tempo do
vapor trocar energia com o meio externo, portanto, consome parte de sua energia interna, o que acarreta
na sua diminuição de temperatura.
Adiabática: Como não há troca de calor com o meio externo, a expansão é considerada adiabática.
Perde: A expansão do gás exige trabalho, na adiabática esse trabalho é absorvido da energia interna do
gás.
14 - Para participar de um importante torneio, uma equipe de estudantes universitários
desenvolveu um veículo aéreo não tripulado. O aparelho foi projetado de tal maneira que ele era
capaz de se desviar de objetos através da emissão e recepção de ondas sonoras. A frequência das
ondas sonoras emitidas por ele era constante e igual a 20 kHz. Em uma das situações da prova
final, quando o aparelho movimentava-se em linha reta e com velocidade constante na direção de
um objeto fixo, o receptor do veículo registrou o recebimento de ondas sonoras de frequência de
22,5 kHz que foram refletidas pelo objeto. Considerando que nesse instante o veículo se
encontrava a 50 m do objeto, assinale a alternativa correta para o intervalo de tempo de que ele
dispunha para se desviar e não colidir com o objeto. Considere a velocidade do som no ar igual a
340 m/s.
FÓRMULAS E VARIÁVEIS:
v som=340 m/ s
v receptor
v emissor
v ±v
f '=f ( som receptor )
v som ±v emissor
Δx
v méd =
Δt
Calculândia – Escola de Reforço para Ensino Médio e Fundamental
Exercícios Resolvidos – FÍSICA ­ UFPR 2014/2015 – 1ª fase
CONTEXTUALIZAÇÃO E TEORIA:
i. Para facilitar o entendimento e a resolução, separa-se o exercícios em dois momentos. 1°)
emissão da onda pelo veículo, sendo o veículo o emissor e o objeto fixo o receptor. 2°) recepção
da onda pelo veículo, sendo o objeto fixo emissor e o veículo receptor (interpretando a reflexão
como emissão de onda pelo objeto fixo).
RESOLUÇÃO:
1° momento:
Pela fórmula do Efeito Doppler, temos:
v som ±v receptor
) , sendo f =20 Hz , v receptor =0 , v emissor =? e v som=340 m/ s
v som ±v emissor
340±0
f ' =20(
) , numa aproximação (convencionando como trajetória positiva o sentido de
340±v emissor
receptor para emissor) a velocidade do emissor é negativa (f'>f). Portanto,
340
f '=20(
)
340−v emissor
2° momento:
f '=f (
v som ±v receptor
) , sendo
f '=22,5 Hz( frequência recebida peloreceptor ,no caso o veículo) ,
v som ±v emissor
v receptor =? e o sinal da velocidade do receptor positiva, já que há aproximação da fonte. Então:
340+ v receptor
a
frequência
“emitida”
(refletida)
pelo
objeto
fixo
é
22,5=f (
) ,
340±0
340
f =f refletida=20 (
) , obtida na primeira parte do exercício. Então:
340−v emissor
340+v receptor
340
22,5=20 (
)(
)
340−v emissor
340±0
Sabemos que no 1° momento, o emissor é o veículo, já no 2° momento, o veículo torna-se receptor.
Assim sendo, neste caso v emissor =v receptor , para simplificar definiremos como v . Portanto,
340
340+ v
22,5=20 (
)(
) ,
340−v
340
resolvendo a equação, temos: v =20 m/ s
Como o veículo segue em velocidade constante, para determinar o tempo nos basta lembrar da equação
Δx
Δx
da velocidade média: v méd =
, ou ainda Δ t=
.
Δt
v méd
f '=f (
Δ t=
50 m
=2,5 s
20 m/ s
Calculândia – Escola de Reforço para Ensino Médio e Fundamental
Exercícios Resolvidos – FÍSICA ­ UFPR 2014/2015 – 1ª fase
15 - Michael Faraday foi um cientista inglês que viveu no século XIX. Através de suas descobertas
foram estabelecidas as bases do eletromagnetismo, relacionando fenômenos da eletricidade,
eletroquímica e magnetismo. Suas invenções permitiram o desenvolvimento do gerador elétrico, e
foi graças a seus esforços que a eletricidade tornou-se uma tecnologia de uso prático. Em sua
homenagem uma das quatro leis do eletromagnetismo leva seu nome e pode ser expressa como:
ε= ∆∅/∆t onde ε é a força eletromotriz induzida em um circuito, ∅ é o fluxo magnético através
desse circuito e t é o tempo. Considere a figura ao lado, que representa um ímã próximo a um anel
condutor e um observador na posição O. O ímã pode se deslocar ao longo do eixo do anel e a
distância entre o polo norte e o centro do anel é d. Tendo em vista essas informações, identifique as
seguintes afirmativas como verdadeiras (V) ou falsas (F):
( F ) Mantendo-se a distância d constante se observará o surgimento de uma corrente induzida no
anel no sentido horário.
Falso, pois não há variação de fluxo magnético para gerar corrente elétrica induzida (Lei de Faraday).
( F ) Durante a aproximação do ímã à espira, observa-se o surgimento de uma corrente induzida
no anel no sentido horário.
Falso, pois ao se aproximar o pólo norte do imã, gera-se na face da espira voltada para o imã um pólo
norte, e, pela regra da mão direita, chega-se a uma corrente no sentido anti-horário.
( V ) Durante o afastamento do ímã em relação à espira, observa-se o surgimento de uma corrente
induzida no anel no sentido horário.
Verdadeiro, ao afastar o pólo norte da espira, gera-se na face da espira voltada para o imã um pólo sul,
e, pela regra da mão direita, determina-se uma corrente no sentido horário.
( V ) Girando-se o anel em torno do eixo z, observa-se o surgimento de uma corrente induzida.
Verdadeiro, pois haverá variação de fluxo magnético que atravessam a bobina e gerar corrente elétrica
induzida.
16 - A função principal de geradores elétricos é transformar em energia elétrica algum outro tipo
de energia. No caso de geradores elementares de corrente contínua, cujo circuito equivalente está
mostrado ao lado, onde r é a resistência interna do gerador e ε sua força eletromotriz, o
comportamento característico é descrito pela conhecida equação do gerador, que fornece a
diferença de potencial ΔV em seus terminais A e B em função da corrente i fornecida por ele. Um
dado gerador tem a curva característica mostrada no gráfico ao lado.
A partir do circuito e do gráfico apresentados, assinale a alternativa correta para a potência
dissipada internamente na fonte quando esta fornece uma corrente de 2,0 mA.
Calculândia – Escola de Reforço para Ensino Médio e Fundamental
Exercícios Resolvidos – FÍSICA ­ UFPR 2014/2015 – 1ª fase
FÓRMULAS E VARIÁVEIS:
Δ v=tensão entre o terminais A e B
ε=força eletromotriz do gerador
r=resistênciainterna do gerador
i=corrente do circuito
Δ v=ε−r . i
P=U . I
U=R . I
RESOLUÇÃO:
Analisando o gráfico no ponto em que Δ v=10 mV e i=0 , e utilizando a fórmula
teremos a seguinte equação do gerador 10.10−3=ε−r .0 , temos:
ε=10 mV
Δ v=ε−r . i
i=8 mA , e, conforme calculado anteriormente
Já para o segundo ponto em que Δ v=0 ,
ε=10 mV . Teremos, portanto, a seguinte equação do gerador
−3
−3
0=10.(10 )−r .8 .(10 )
r=
10
Ω
8
Para calcular a potência elétrica dissipada internamente utilizamos a fórmula P=U . I , para isso,
precisamos calcular o valor de U , utilizamos, então, U=R . I , e a substituímos na equação da
potência:
2
P=(R . I ). I =R . I
10
−3 2
P= .(2.10 )
8
−6
P=5.10 W ou P=5μ W
17 - Considere as seguintes afirmativas relacionadas aos fenômenos que ocorrem com um feixe
luminoso ao incidir em superfícies espelhadas ou ao passar de um meio transparente para outro:
1. Quando um feixe luminoso passa do ar para a água, a sua frequência é alterada.
Falso, apenas a velocidade e a direção podem se alterar.
2. Um feixe luminoso pode sofrer uma reflexão interna total quando atingir um meio com índice de
refração menor do que o índice de refração do meio em que ele está se propagando.
Verdadeiro.
3. O fenômeno da dispersão ocorre em razão da independência entre a velocidade da onda e sua
frequência.
Falso, ocorre pela diferença de cada comprimento de onda que compõem a luz branca. Ondas de
frequências diferentes se propagam com velocidades diferentes em diferentes meios.
4. O princípio de Huygens permite explicar os fenômenos da reflexão e da refração das ondas
luminosas.
Verdadeira, para explicar a onda, Huygens estabelece que cada ponto final de uma onda se comporta
como uma nova fonte de onda com mesma frequência do ponto anterior.
Calculândia – Escola de Reforço para Ensino Médio e Fundamental
Exercícios Resolvidos – FÍSICA ­ UFPR 2014/2015 – 1ª fase
18 - No final do século XIX e início do século XX, a Física se defrontou com vários problemas que
não podiam ser explicados
com as teorias e modelos aceitos até esse período. Um desses problemas consistia em explicar
corretamente o
fenômeno do Efeito Fotoelétrico. Sobre esse efeito, considere as seguintes afirmativas:
1. Esse efeito foi observado primeiramente por Henrich Hertz e sua explicação correta foi
publicada em 1905 por Niels Bohr.
Falso, O primeiro a observar o efeito fotoelétrico foi o físico francês Alexandre Edmond Becquerel, e
quem o explicou de forma satisfatória foi físico alemão Albert Einstein.
2. A explicação correta desse efeito utilizou uma ideia de Max Planck, de que a luz incidente não
poderia ter energia com um valor qualquer, mas sim uma energia dada por múltiplos inteiros de
uma porção elementar.
Verdadeira, essa porção elementar é chamada de Quantum.
3.Segundo o modelo proposto, cada fóton, ao colidir com um elétron, transfere-lhe uma
quantidade de energia proporcional a sua velocidade.
Falso, essa explicação é a que se esperava quando tratava-se o efeito sobre a luz da física clássica.
Porém, não é isso o que ocorre, a energia é proporcional à sua frequência, conforme disposto pela
equação E=h. f , em que h=constante de Planck