função do 2º grau e Polígonos

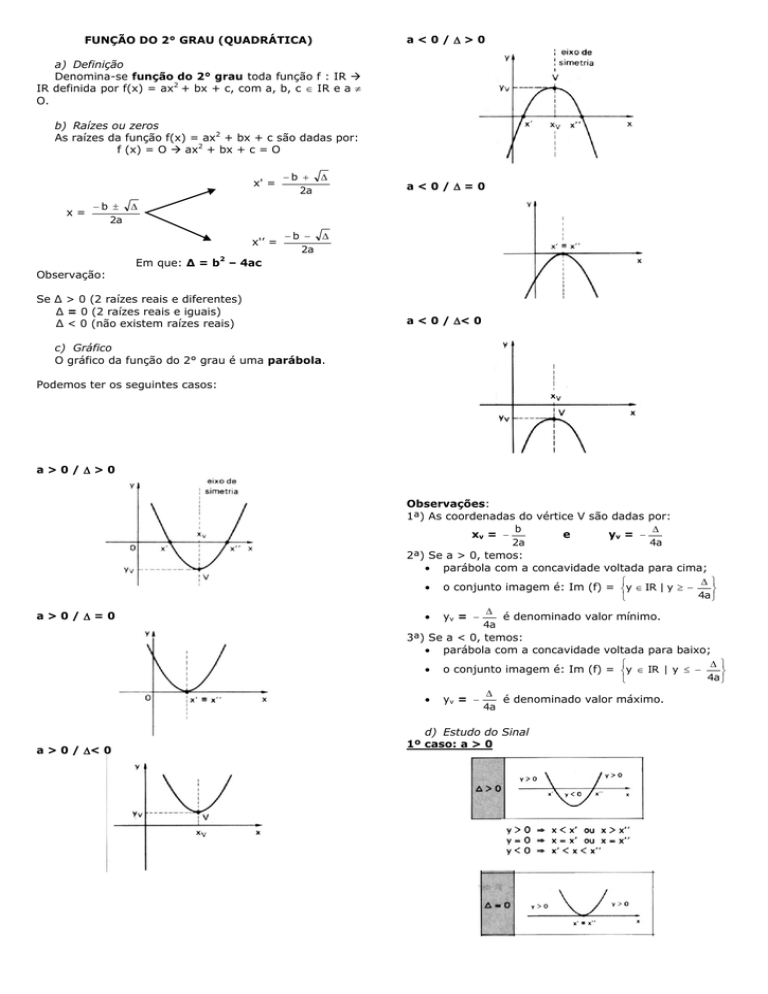
FUNÇÃO DO 2° GRAU (QUADRÁTICA)
a<0/>0
a) Definição
Denomina-se função do 2° grau toda função f : IR 
IR definida por f(x) = ax2 + bx + c, com a, b, c  IR e a 
O.
b) Raízes ou zeros
As raízes da função f(x) = ax2 + bx + c são dadas por:
f (x) = O  ax2 + bx + c = O
x=
x' =
b  
2a
x'’ =
b  
2a
a<0/=0
b  
2a
Observação:
Em que: Δ = b2 – 4ac
Se Δ > 0 (2 raízes reais e diferentes)
Δ = 0 (2 raízes reais e iguais)
Δ < 0 (não existem raízes reais)
a < 0 / < 0
c) Gráfico
O gráfico da função do 2° grau é uma parábola.
Podemos ter os seguintes casos:
a>0/>0
Observações:
1ª) As coordenadas do vértice V são dadas por:
xv = 
b
2a
e
yv = 

4a
2ª) Se a > 0, temos:
 parábola com a concavidade voltada para cima;

a>0/=0


o conjunto imagem é: Im (f) = y  IR | y  


yv = 
é denominado valor mínimo.
4a


4a 
3ª) Se a < 0, temos:
 parábola com a concavidade voltada para baixo;
a > 0 / < 0


o conjunto imagem é: Im (f) = y  IR | y  

yv = 


é denominado valor máximo.
4a
d) Estudo do Sinal
1º caso: a > 0
 

4a 
cartesiano nos mesmos pontos, conforme mostra o
gráfico. Qual é a equação da reta?
05. O gráfico da função y = ax2 + bx + c é a parábola da
figura abaixo. Os valores de a, b e c são,
respectivamente:
2º caso: a < 0
a) 1, – 6 e 0
d) –1, 6 e 0
b) – 5, 30 e 0
e) – 2, 9 e 0
c) – 1, 3 e 0
06. O lucro de uma empresa é dado por L(x) = - 10x2 +
120x – 200, onde x é a quantidade vendida. Para que
valor de x obtém lucro máximo?
07. Uma bola é lançada ao ar. Suponha que a altura H,
em metros, t segundos após o lançamento, seja H =
- t2 + 4t + 6. Pede-se:
a) Em que instante a bola atinge a sua altura
máxima?
b) Qual é a altura máxima atingida pela bola?
08. Uma empresa de turismo promove um passeio para
N pessoas, no qual cada pessoa paga uma taxa de
(100 – N) reais. Nestas condições, o dinheiro total
arrecadado pela empresa varia em função do número
N. qual a maior quantia que a empresa pode
arrecadar?
EXERCÍCIOS:
01. Com respeito a função quadrática f(x) = ax2 + bx +
c, com a  0, não é correto afirmar que:
a) Se a > 0, a concavidade da parábola está
voltada para cima.
b) Se  = 0, existem duas raízes reais e iguais.
c) Se c = 0, então uma das raízes necessariamente será nula.
d) Se b = c = 0, então a função tem um gráfico que
é simétrico ao eixo de y.
e) Se a < 0, então existe um mínimo dado pelo
vértice da parábola.
09. Suponha que numa fábrica de refrigeradores o custo,
em R$, de cada geladeira é dado pela função C(x) =
x2 – 40x + 500, em que x é a quantidade de
geladeiras produzidas.
0 0 1)
Quando se produzem 10 geladeiras, o
custo de cada geladeira é de R$ 200,00;
1 1 A produção de 20 geladeiras é a que
proporciona o menor custo de cada geladeira;
2 2 O conjunto imagem da função anteriormente
definida é qualquer número real não negativo;
3 3 A função Ct(x) = x3 – 40x2 + 500x representa o
custo total de produção quando se produzem x
geladeiras.
4 4 O custo total para se produzirem 50 geladeiras
é de R$ 1000,00.
10. O gráfico abaixo representa uma função quadrática
f(x) = ax2 + bx + c. Então:
02. Determine M para que a função dada por f(x) = x2 –
3x + M tenha duas raízes reais e distintas.
03. Determine P a fim de que o gráfico de f(x) = 2x2 + x
+ (P – 1) não intercepte o eixo das abscissas.
04. A parábola no gráfico ao lado é dada pela função f(x)
= x2 – 4x + 3. A reta e a parábola cruzam o eixo
0
0
O vértice é o ponto (- 1, 4)
1
2
3
4
1
2
3
4
A função cresce no intervalo x > - 1
a+b+c=0
f(3) = - 10
A função é uma função par
11. Num vôo com capacidade para 100 pessoas uma
companhia aérea cobra R$ 200,00 por pessoa
quando todos os lugares são ocupados. Se existirem
lugares não ocupados, ao preço de cada passagem
será acrescida a importância de R$ 4,00 por cada
lugar não ocupado (por exemplo, se existirem 10
lugares não ocupados o preço de cada passagem será
R$ 240,00). Quantos devem ser os lugares não
ocupados para que a companhia obtenha o
faturamento máximo?
12. Uma loja de discos vende 3.000 cds por mês a um
preço de R$13,00 a unidade. Uma pesquisa de
mercado concluiu que, a cada aumento de R$ 0,50
no preço de cada cd, as vendas caem de 100 cds
por mês. Qual deve ser o preço de cada cd, para se
maximizar o valor total das vendas?
a) R$13,50
b) R$14,00
c) R$14,50
d) R$15,00
e) R$15,50
a) 3
c) 12
d) 13
e) 15
19. Quando o preço do sanduíche é de R$ 4,00, uma
lanchonete vende 150 unidades por dia. O número de
sanduíches vendidos diariamente aumenta de 5
unidades, a cada diminuição de R$ 0,10 no preço de
cada sanduíche. Para qual preço do sanduíche, a
lanchonete arrecadará o maior valor possível com a
venda diária dos sanduíches?
a) R$ 3,10
b) R$ 3,20
c) R$ 3,30
d) R$ 3,40
e) R$ 3,50
20. Uma ponte possui um arco de sustentação na forma
de um arco de parábola com eixo passando por OQ e
suportes verticais situados a uma mesma distância,
conforme ilustração a seguir. O comprimento da
ponte é de 20m e a maior distância entre pontos do
arco e a ponte é de 5m. O ponto P dista 5m do
centro da ponte e PM é perpendicular à ponte.
Determine a distância PM, em metros, e indique 4 
PM.
Q
M
5
13. A parábola de equação y = - 2x2 + bx + c passa pelo
ponto (1, 0) e seu vértice é o ponto de coordenadas
(3, V). Determine V.
14. Uma malharia familiar fabrica camisetas a um custo
de R$ 2,00 por camiseta e tem uma despesa fixa de
R$ 50,00.
Se são vendidas x camisetas por semana ao preço de
b) 10
O
5
5
P
5
5
21. O gráfico abaixo representa uma função polinomial
do 2º grau y = p(x), que corta o eixo das abscissas
em x = – 1 e x = 2, tal que p
( 0 ) = – 2.
x 
 22



30 
 3
reais a unidade, quantas camisetas devem
ser vendidas por semana para se obter o maior lucro
possível?
a) 50
b) 60
c) 65
d) 90 e) 80
15. Uma loja de departamentos vende uma camisa por
R$ 20,00 e 100 unidades desta camisa por mês.
Observou-se que para cada real de desconto no preço
da camisa as vendas aumentaram em 10 unidades
por mês. Quanto deve ser o desconto em reais, de
modo a se obter um faturamento mensal máximo na
venda deste modelo de camisa?
16. Quando o preço do pão francês era de R$ 0,12 a
unidade, uma padaria vendia 1000 unidades
diariamente. A cada aumento de R$ 0,01 no preço
de cada pão, o número de pães vendidos por dia
diminui de 50 unidades.
Reajustando adequadamente o preço do pão, qual a
quantia máxima (em reais) que pode ser arrecadada
diariamente pela padaria com a venda dos pães?
Assinale metade do valor correspondente à quantia
obtida.
17. Suponha que o consumo de um carro para percorrer
100km com velocidade de x km/h seja dado por C(x)
= 0,006x2 - 0,6x + 25. Para qual velocidade este
consumo é mínimo?
a) 46km/h
b) 48km/h
c) 50km/h
d) 47km/h
e) 49km/h
18. Em uma fabrica, o custo de produção de x produtos é
dado por c(x) = - x2 + 22x +1. Sabendo-se que cada
produto é vendido por R$ 10,00, o número de
produtos que devem ser vendidos para se obter um
lucro de R$ 44,00 é:
0
1
2
3
0
1
2
3
O valor mínimo de p(x) é y = – 2.
p(x) = x2 – x – 2
p(x) > 0 se x < – 1 ou x > 2
A soma dos coeficientes de p (x) é (– 2 ).
4
4
A imagem de p (x) é  ,  
 4 
 9

22. Um fazendeiro queria construir um cercado em forma
de um retângulo para criar gado. Como o dinheiro
que ele tinha era suficiente para fazer apenas 200
metros de cerca, resolveu aproveitar uma parte reta
da cerca do vizinho para economizar e construiu, com
apenas 3 lances de cerca, um cercado retangular de
área máxima. Qual a área deste cercado?
a) 5100 m2
b) 5000 m2
c) 4900 m2
2
2
d) 5300 m
e) 5200 m
23. Em um terreno retangular de 90m de perímetro,
Maria Eduarda pretende construir um galpão para
depósito de sua fábrica de confecções. O código de
obras da cidade exige que sejam dados recuos de 2m
na frente e nos fundos e 1,5m em cada lateral.
Podemos afirmar que a área máxima do galpão, em
metros quadrados, é:
a) 361;
b) 456;
c) 506;
d) 650;
e) 546.
24. Observando a figura abaixo, qual o perímetro do
retângulo de área máxima inscrito no triangulo
isósceles de base 4 cm e altura 6 cm.
Analise
0 0
1 1
2 2
3
4
a) 8cm
b) 10cm
c) 12cm
d) 9cm
e) 11cm
3
4
a veracidade das afirmações seguintes:
p(x) admite duas raízes reais.
b>0
p(x) define uma função decrescente para
todo real x.
p(x) < 30 para todo real x.
c > 0.
GABARITO:
01) E
25. A figura abaixo ilustra parte do gráfico de um
polinômio quadrático p(x) = ax2 + bx + c com
coeficientes a, b e c reais.
25
20
15
10
5
-3
-2
-1
0
-5
1
x
2
3
06) 06
02) M < 9/4 07) a) 02
07) b) 10
03) P > 9/8 08) 2500
reais
04) y = -x + 09) FVFVF
3
05) D
10) VFVFV
11) 25 16)
64
12) B
17) C
21) FVVVV
13) 08 18) E
23) A
14) E
24) B
19) E
15) 05 20)
15
22) B
25) VFFFV
POLÍGONOS
Definição
Considerando, num plano, n pontos (n > 3), A1 , A2,
A3,...... , A n, ordenados de modo que três consecutivos
não sejam colineares.
Chama-se polígono A1 , A2 , A3,....., A n à figura
formada pela união dos n segmentos consecutivos :
A1A2  A2A3  A3A4  .......  A nA1
Região poligonal:
É a região determinada pela união do polígono com os
pontos de sua região interior
Chama-se diagonal de um polígono a todo segmento
de reta cujas extremidades são vértices não consecutivos.
Num polígono de n lados:
a) cada vértice dá origem a ( n - 3 ) diagonais
b) os n vértices dão origem a n . ( n - 3 ) diagonais.
c) com este raciocínio, cada diagonal foi contada duas
vezes, pois cada uma delas é determinada por dois
vértices.
Assim, sendo d o número de diagonais do polígono
temos :
d=
n (n - 3)
2
Observe que, o polígono tem 7 lados e que cada vértice
da origem a 7 - 3 = 4 diagonais.
Soma dos ângulos internos:
Seja um polígono de n lados e P um ponto interno.
Ligando P aos vértices, obtemos n triângulos cuja soma
dos ângulos internos é 180o.n.
Assim, sendo Si a soma dos ângulos internos do
polígono, temos:
Polígono convexo:
É o polígono cuja região poligonal é convexa
Um polígono convexo com n lados tem: n vértices, n
ângulos internos e n ângulos externos.
Observação: Estudaremos somente polígonos convexos.
Nomenclatura
De acordo com o número de lados, temos:
triângulo (3 lados) - quadrilátero (4 lados)
pentágono (5 lados) - hexágono (6 lados)
heptágono (7 lados) - octógono (8 lados)
eneágono (9 lados) - decágono (10 lados)
undecágono (11 lados) - dodecágono (12 lados)
pentadecágono (15 lados) - icoságono - (20 lados)
Si = 180o. n - 360o.
 Si = ( n - 2 ) . 180o.
Genericamente utiliza-se o termo polígono de n
lados.
Classificação
Polígono eqüilátero: É o polígono que tem todos os
lados congruentes. Ex.: Losango, quadrado, etc.
Polígono eqüiângulo: É o polígono que tem todos os
ângulos internos congruentes. Ex.: Retângulo, quadra-do,
etc.
Polígono regular: É o polígono que é eqüilátero e
eqüiângulo simultaneamente. Ex.: Quadrado.
Observe que: o losango da figura é eqüilátero mas não é
eqüiângulo e que o retângulo da figura é eqüiângulo mas
não é eqüilátero.
Número de diagonais:
A soma dos ângulos internos do polígono da figura
é:
Sn = (6 . 180o) - 360o = 720o
Soma dos ângulos externos:
Sejam, num polígono de n lados, ai e ae,
respectivamente, as medidas de um ângulo interno e do
ângulo externo adjacente a ele, Si a soma dos ângulos
internos e Se a soma dos ângulos externos.
Sendo ai + ae = 180o., para cada um dos vértices do
polígono, temos:
Si + Se = 180o. n  180o. n - Si 
Se = 180o. n - (n - 2) . 180  Se = 360o
Se o polígono for eqüiângulo, todos os ângulos
internos são congruentes e todos os ângulos externos são
congruentes e, portanto.
ai = Si / n
ae = Se / n
A soma das quantidades
polígonos é:
a) 9
b) 13
c) 17
de
diagonais
d) 20
destes
e) 23
11. Calcule, em graus a soma dos ângulos assinalados na
figura seguinte:
ai1 + ae1 = ai2 + ae2 = a3 +ae3 = ai4 + ae4 = ai5 + ae5 =
180o. Assim sendo:
Si + Se = 180o. 5  Se = 900o.- (5 - 2) . 180o.  Se =
360o.
EXERCÍCIOS
01. Calcule o número de diagonais de um eneágono
12. A soma dos ângulos assinalados na figura vale:
a) 90º
b) 180º
c) 270º
d) 360º
e) 540º
convexo.
02. Qual o polígono convexo cujo número de diagonais é
o dobro do número de lados?
03. A soma dos ângulos internos de um heptágono
convexo é:
a) 360º
b) 540º
c) 1400º
d) 900º
e) 180º
04. Qual a medida do ângulo interno de um hexágono
regular?
13. Num polígono regular ABCDE......, a diagonal AC
forma com o lado CB um ângulo de 18o. Esse polígono
possui:
a) 20 diagonais
b) 20 lados
c) 40 diagonais
d) 18 lados
e) 35 diagonais
05. Cada um dos ângulos internos de um polígono regular
mede 150o. Qual é o número de lados do polígono?
06. Cada um dos ângulos externos de um polígono
regular mede
polígono?
15o.
Quantas
diagonais
tem
esse
Num polígono regular, a medida de cada ângulo
interno supera a medida de cada ângulo externo em
108º. Calcule o número de lados desse polígono.
07. Quantos lados tem um polígono convexo, cujo número
14.
08. Num polígono convexo de n lados sejam: ai e ae,
15.
Qual o polígono convexo que tem exata-mente 20
diagonais?
a) Hexágono.
b) Heptágono.
c) Octógono.
d) Eneágono.
e) Decágono
16.
Num polígono regular o número de diagonais é igual
ao número de lados. A medida de cada um dos
ângulos internos desse polígono é:
a) 60º
b) 90º
c) 105º
d) 108º
e) 120º
17.
cinco vezes a soma dos ângulos externos. Calcule o
número de diagonais desse polígono.
Qual o polígono regular cuja medida do ângulo
externo é a metade da medida do ângulo interno?
a) Octógono regular.
b) Hexágono regular.
c) Pentágono regular.
d) Quadrado.
e) Triângulo eqüilátero.
10. A soma dos ângulos internos de dois polígonos cujos
18. Na figura seguinte tem-se um pentágono regular
de diagonais é d e a soma dos ângulos internos é
180o. d?
respectivamente, as medidas de um dos ângulos
internos e do ângulo externo adjacente a ele, Si a
soma dos ângulos internos, Se a soma dos ângulos
externos e d o número de diagonais.
Assim:
I II
0 0
ai + ae = 180o.
1 1
Si = (n - 2) . 180o.
2 2
Se = 360o.
3 3
d = n . (n - 3) / 2
4 4
Se o polígono for eqüiângulo temos:
ai = Si / n
ae = Se / n
09. Num polígono convexo a soma dos ângulos internos é
números de lados são inteiros e consecutivos é 1620o.
ABCDE onde estão traçadas todas as suas diagonais.
A medida do ângulo DAE é:
a) 24º
b) 30º
c) 36º
d) 45º
e) 72º
19. As mediatrizes de dois lados consecutivos de um
polígono regular formam um ângulo de 20º. Esse
polígono é um:
a) Octógono regular.
b) Eneágono regular.
c) Decágono regular.
d) Pentadecágono regular.
e) Octadecágono regular.
20. São dados dois polígonos regulares. O segundo tem 4
lados a menos que o primeiro e o ângulo externo do
segundo excede o ângulo externo do primeiro em 45º.
O número de lados do primeiro polígono é:
a) 6
b) 8
c) 10
d) 12
e) 20
21. O menor ângulo interno de um paralelogramo mede
40º. Qual a medida do maior ângulo interno desse
paralelogramo?
a) 50º
b) 90º
c) 12º
d) 130º
e) 140º
22. Num trapézio retângulo, a medida do maior ângulo
interno é o quádruplo da medida do menor dos
ângulos internos desse trapézio é:
a) 30º
b) 36º
c) 45º
d) 72º
e) 90º
23. Qual a medida do ângulo formado pelas bissetrizes de
dois
ângulos
internos
não
opostos
de
paralelogramo?
a) 30º
b) 45º
c) 60º
d) 75º
e) 90º
um
24. Em um trapézio isósceles, a altura é igual à base
média. Assim, o ângulo que a diagonal forma com a
base é:
a) 15º
b) 22º 30´
c) 30º
d) 45º
e) 60º
25. Na ilustração abaixo, os segmentos AB e EF são
paralelos. Determine a soma S, em graus, dos
ângulos indicados com vértices nos pontos B, C, D e
E. Indique S/10.
B
A
C
D
E
F