onde n³ l+1, n é o número quântico principal e En corresponde aos

Física Atómica e Nuclear – Capítulo 2.
Átomos de Um Electrão
32
Bohr chegou aos mesmos resultados através da sua teoria. Este resultado é
importante porque veio a confirmar a teoria da Mecânica Quântica de Schrödinger. A
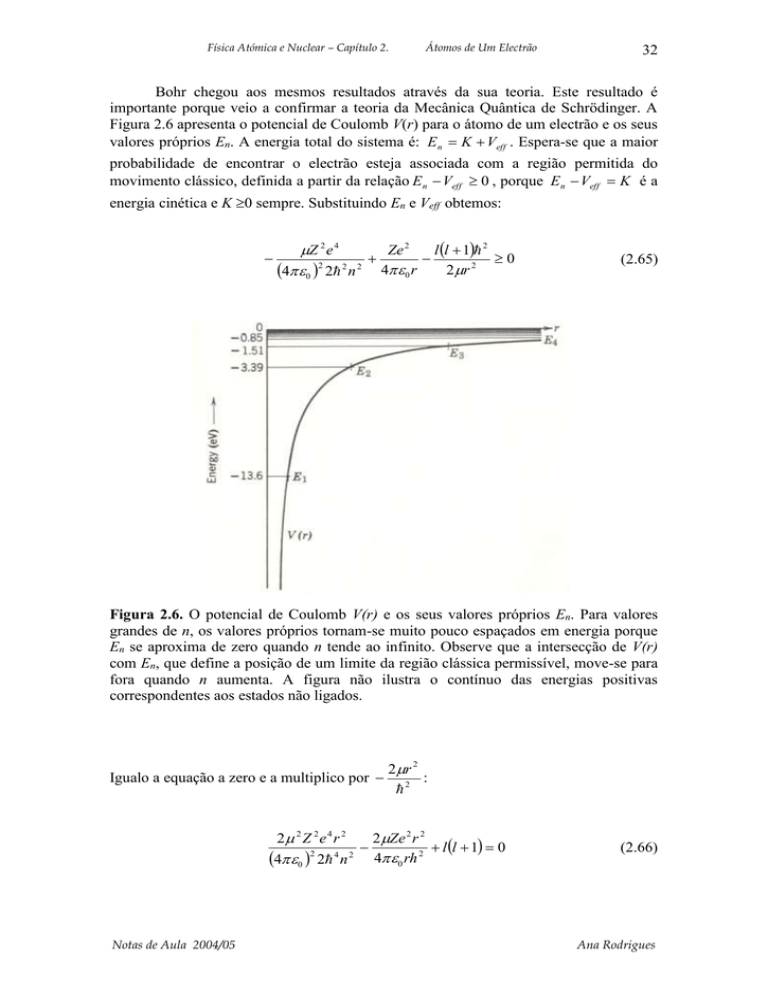
Figura 2.6 apresenta o potencial de Coulomb V(r) para o átomo de um electrão e os seus
valores próprios En. A energia total do sistema é: E n  K  Veff . Espera-se que a maior
probabilidade de encontrar o electrão esteja associada com a região permitida do
movimento clássico, definida a partir da relação E n  Veff  0 , porque E n  Veff  K é a
energia cinética e K 0 sempre. Substituindo En e Veff obtemos:

Z 2 e 4
Ze 2
l l  1 2


0
40 2 2 2 n 2 40 r 2r 2
(2.65)
Figura 2.6. O potencial de Coulomb V(r) e os seus valores próprios En. Para valores
grandes de n, os valores próprios tornam-se muito pouco espaçados em energia porque
En se aproxima de zero quando n tende ao infinito. Observe que a intersecção de V(r)
com En, que define a posição de um limite da região clássica permissível, move-se para
fora quando n aumenta. A figura não ilustra o contínuo das energias positivas
correspondentes aos estados não ligados.
Igualo a equação a zero e a multiplico por 
2 2 Z 2 e 4 r 2
40 2 2 4 n 2
Notas de Aula 2004/05

2r 2
:
2
2Ze 2 r 2
 l l  1  0
40 rh 2
(2.66)
Ana Rodrigues
Física Atómica e Nuclear – Capítulo 2.
substituo
Átomos de Um Electrão
33
40  2
 a0 :
e 2
Z 2 r 2 2Zr

 l l  1  0
a0
a02 n 2
(2.67)
ou
r2  2
a0 n 2
a n2
r  0 2 l l  1  0
Z
Z
(2.68)
Esta equação é uma equação de segundo grau, cujas raízes são:
r1, 2  a0

n
n  n 2  l l  1
2Z

(2.69)
e r está situado entre a raiz r1 e r2. Significa que num estado estacionário definido pelos
números quânticos n e l, o electrão estará localizado com uma probabilidade máxima
a n2
an
numa região de largura r  r1  r2  0 n 2  l l  1 em torno do valor rn  0 .
Z
Z
Para n=1 e Z=1, rn=a0 e o electrão move-se numa região esférica bem definida pelo raio
de Bohr.
Figura 2.7. Região permitida do movimento clássico.
Notas de Aula 2004/05
Ana Rodrigues
Física Atómica e Nuclear – Capítulo 2.
Átomos de Um Electrão
34
É importante observar que enquanto os valores próprios do átomo de um
electrão dependem somente do número quântico n, as funções próprias dependem de
todos os três números quânticos uma vez que corresponde ao produto das três funções
m
Rnl, Pl u  e m( ). O aparecimento dos números quânticos é uma consequência do
facto de que a equação de Schrödinger independente do tempo contém três variáveis
independentes, uma para cada coordenada espacial.
Concluímos que os valores permitidos dos números quânticos, associados às
soluções aceitáveis da equação de Schrödinger em coordenadas esféricas são:
n = 1, 2, 3.... para E n  
Z 2 e 4
40 2 2 2 n 2
l  0,1,2,..., n  1 para L  l l  1
m  l ,l  1,...,0,...,l  1, l
para
(2.70)
Lz  m
2.6 Funções Próprias. Degenerescência. Densidade de Probabilidade.
As funções próprias dão uma série de informações sobre as propriedades do átomo.
As funções próprias do átomo de um só electrão são:
 nlm r , ,    Rnl r Pl|m| cos  m  
(2.71)
e satisfazem a equação de Schrödinger:

 2  1   2  
1
 2
1
 
 
r

 2


 sin 
  V r   E
 2
2
2
2
2  r r  r  r sin  
 
r sin   
(2.72)
Em geral, para um determinado valor de n, temos vários valores possíveis para l
e m, como já vimos em (2.70). Como a forma das funções próprias dependem de todos
os números quânticos, poderá haver o caso em que funções próprias diferentes
corresponderão a um mesmo valor de energia En, e uma vez que as funções próprias
descrevem o comportamento do átomo, existirá estados com comportamentos
totalmente diferentes, mas que têm a mesma energia total. A física chama a este
fenómeno de degenerescência e a funções próprias correspondentes ao mesmo
valor próprio são chamadas de degeneradas.
A degenerescência ocorre tanto na mecânica clássica como na antiga teoria
quântica a ela relacionada. Para as órbitas elípticas do átomo de Bohr- Sommerfeld, um
electrão descreve órbitas diferentes, mas com a mesma energia total. O mesmo se passa
com os sistemas planetários. Esta degenerescência clássica é comparável à
degenerescência em l, que acontece no átomo de um electrão da mecânica quântica. A
energia de um átomo de Bohr – Sommerfeld ou do sistema planetário também não
Notas de Aula 2004/05
Ana Rodrigues
Física Atómica e Nuclear – Capítulo 2.
Átomos de Um Electrão
35
depende da orientação espacial do plano da órbita, o que corresponde a degenerescência
m do átomo da mecânica quântica.
Através de (2.70) podemos saber quantas funções próprias degeneradas existem
para um átomo de um electrão isolado, correspondente a um valor particular de En. A
partir da Tabela 2.1, que mostra todos os números quânticos possíveis para n=1, 2 e 3,
concluímos que:



Para cada n, existem n valores possíveis de l.
Para cada valor de l, existem (2l+1) valores possíveis de m.
Para cada valor de n, existe um total de n2 funções próprias degeneradas.
Todas as funções próprias têm basicamente a mesma estrutura matemática, embora
os polinómios em r e cos aumentem de complexidade para valores crescentes de n e l.
A Tabela 2.2 mostra as funções próprias para até n = 3.
Agora vamos extrair informações das funções próprias analisando as formas das
funções densidade de probabilidade Pnlm r , ,  correspondentes.
A probabilidade de encontrar um electrão, descrito pela função de onda
 nlm r , ,   , num elemento de volume dV  r 2 drd é:
Pnlm r , ,  dV  =  nlm r , ,   r 2 drd  Rnl r  Ylm  ,  r 2 drd
2
2
(2.73)
Tabela 2.1. Valores possíveis de l e m, para n=1,2,3.
onde Ylm  ,   = Pl|m| cos    m   , localiza o electrão dentro de um ângulo sólido
2
2
2
d  sin dd , em torno da origem.
Então:
Pnlm r , ,  dV  = Rnl r  Pl|m| cos   m   r 2 drd
2
Notas de Aula 2004/05
2
2
(2.74)
Ana Rodrigues
Física Atómica e Nuclear – Capítulo 2.
Átomos de Um Electrão
36
A densidade de probabilidade é independente de , porque:
 m     m    m   
2
*
1  im
1 im
1
e

e 
2
2
2
(2.75)
*
 nlm é completamente especificado
Logo, o comportamento tridimensional de Pnlm   nlm
pelo produto das funções radiais Rnl* r Rnl r   Pnl r  / 4 2 e pelas funções de Legendre
associadas Pl | m| cos   *lmlm . Esta última desempenha o papel de factor de
2
modulação relativamente à direcção. Veja Figura 2.8.
Tabela 2.2. Algumas funções próprias do átomo de um electrão.
Notas de Aula 2004/05
Ana Rodrigues
Física Atómica e Nuclear – Capítulo 2.
Átomos de Um Electrão
37
Na Figura 2.8 ilustramos um exemplo da dependência da forma:
 lm  lm  Pl|m| cos  
2
(2.76)
Figura 2.8. Um gráfico polar que determina a dependência direccional da densidade de
probabilidade do átomo de um electrão.
(a)
(b)
Figura 2.9. Diagramas polares da dependência direccional das densidades de
probabilidade do átomo de um electrão para: a) l=3, ml ( m)  0,1,2,3 b) l=0,1,2,3
e ml ( m)  l.
A densidade de probabilidade radial Rnl r  r 2 representa a densidade electrónica em
função de r ao longo de uma determinada direcção e a função de distribuição radial:
2
Pnl r dr  Rnl r  r 2 dr
2
(2.77)
e corresponde a probabilidade de se encontrar o electrão entre r e r+dr. O volume
compreendido entre as esferas é proporcional a r2. A Figura 2.10 mostra a densidade de
probabilidade radial para os átomos de um electrão com n = 1, 2, 3. Podemos observar
que para um dado conjunto pertinente de números quânticos, Pnl r  só tem valores
apreciáveis em intervalos relativamente reduzidos da coordenada radial. O electrão se
encontrará provavelmente dentro de uma camada contida entre duas esferas
concêntricas e centradas no núcleo e o raio característico desta camada é determinado
Notas de Aula 2004/05
Ana Rodrigues
Física Atómica e Nuclear – Capítulo 2.
Átomos de Um Electrão
38
fundamentalmente pelo número quântico n, embora exista uma pequena dependência
em l.
Figura 2.10. Densidade de probabilidade radial para o electrão num átomo de um
electrão para n=1,2,3 e valores de l indicados nos gráficos.
Podemos caracterizar o raio da camada pelo cálculo do valor esperado:

r
nl
2
  r Pnl dr   Rnl r  r 3dr
(2.78)
0
Substituindo as funções radiais normalizadas obtemos:
r
Notas de Aula 2004/05
nl
n 2 a0  1  l l  1 

1  1 

Z  2 
n 2  
(2.79)
Ana Rodrigues