r - Professores da UFF

GEOMETRIA BÁSICA 2010-2
GGM00161-TURMA M2
Dirce Uesu Pesco
Geometria Espacial
23/11/2010
POLIEDROS CONVEXOS
Aula de 18 novembro:
-
Prisma
-
Pirâmide
-
Poliedro convexo:
POLIEDROS CONVEXOS
Poliedro Convexo:
Considere um número finito n, n  4, de polígonos planos convexos ( ou região
poligonal convexa) tais que:
a) dois polígonos não estão em um mesmo plano;
b) cada lado do polígono é comum a dois e somente dois polígonos;
c) o plano de cada polígono deixa os demais num mesmo semi-espaço.(condição de convexidade)
Nessas condições, ficam determinados n semi-espaços , cada um dos quais
tem origem no plano de um polígono e contem os restantes.
A interseção desses semi-espaços é chamado Poliedro convexo.
POLIEDROS CONVEXOS
Quais dos exemplos abaixo são poliedros, poliedros convexos ?
a)poliedro, não convexo
d)Poliedro convexo
b) não é poliedro
e) poliedro convexo
c) poliedro não convexo
f) não é poliedro
f) não é poliedro
POLIEDROS CONVEXOS
Elementos do poliedro convexo:
Faces: são os polígonos;
Arestas: são os lados dos polígonos;
Vértices : sãos os vértices dos polígonos;
Ângulos : são os ângulos dos polígonos.
PROPRIEDADE DE POLIEDROS CONVEXOS
Teorema de Euler
Para todo poliedro convexo vale a relação:
V  A  F 2
onde
V é o número de vértice, A é o número de arestas e F o número de faces do
poliedro convexo.
Exemplo: Verifique se vale a relação de Euler para os poliedros abaixo:
a)
b)
PROPRIEDADE DE POLIEDROS CONVEXOS
Exemplo 2 : Vale a relação de Euler para os poliedros abaixo?
a)
b)
Poliedro Euleriano: poliedros para os quais vale a relação de Euler.
Todo poliedro convexo é euleriano, mas nem todo poliedro euleriano é convexo.
PROPRIEDADE DE POLIEDROS CONVEXOS
A soma dos ângulos de todas as faces de um poliedro convexo
é:
S  (V  2)  4r
onde V é o número de vértices e r é o ângulo reto.
PROPRIEDADE DE POLIEDROS CONVEXOS
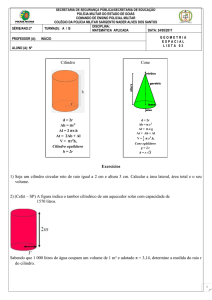
Exercício2 : Calcule a área lateral do prisma obliquo de base
quadrada, cujas medidas estão indicadas na figura.
Unidade : centímetros.
Solução:
PROPRIEDADE DE POLIEDROS CONVEXOS
Exercício2 : Calcule a área lateral do prisma obliquo de base
quadrada, cujas medidas estão indicadas na figura.
Unidade : centímetros.
Solução: São quatro paralelogramos que
compõem as arestas laterais, cuja base é:
3 cm, a altura corresponde a
h  5 sen 60
o
h
5 3
2
 Al  4  Aparalelogramo  Al  4  3. 5 3  30 3 cm 2
2
Exercício: encontre a área total e o volume do prisma
PROPRIEDADE DE POLIEDROS CONVEXOS
OBS:
Seja P um poliedro convexo, com n número de faces e q o número de
arestas que concorrem em cada vértice:
1)
Como cada aresta é lado de exatamente duas faces, então n.F = 2 A
2)
Como cada aresta contém dois vértices, então q.V = 2 A
Exemplo: Um poliedro convexo de 11 faces tem 6 faces triangulares e 5
faces quadrangulares. Determine o número de arestas e de vértices desse
poliedro.
Solução:
PROPRIEDADE DE POLIEDROS CONVEXOS
OBS:
Seja P um poliedro convexo, com n número de faces e q o número de
arestas que concorrem em cada vértice:
1)
Como cada aresta é lado de exatamente duas faces, então n.F = 2 A
2)
Como cada aresta contém dois vértices, então q.V = 2 A
Exemplo: Um poliedro convexo de 11 faces tem 6 faces triangulares e 5
faces quadrangulares. Determine o número de arestas e de vértices desse
poliedro.
Solução:
6 F3  5F4  2 A
 6  3  5  4  2A 
 38  2 A  A  19
V  A  F  2  V  19  11  2  V  10.
POLIEDROS REGULARES
Definição:
Poliedro regular é um poliedro convexo em que as faces são polígonos regulares congruentes e que em todos os vértices concorrem o mesmo número
de arestas.
POLIEDROS REGULARES
Definição:
Poliedro regular é um poliedro convexo em que as faces são polígonos regulares congruentes e que em todos os vértices concorrem o mesmo número
de arestas.
Teorema: Existem apenas cinco poliedros regulares.
http://www.uff.br/cdme/platonicos/platonicos-html/solidos-platonicos-br.html
POLIEDROS REGULARES
Definição:
Poliedro regular é um poliedro convexo em que as faces são polígonos regulares congruentes e que em todos os vértices concorrem o mesmo número
de arestas.
Teorema: Existem apenas cinco poliedros regulares.
i) 4 faces
ii) 6 faces
iii) 8 faces
ii) cubo (hexaedro regular),
i) tetraedro regular,
iv) 12 faces
v) 20 faces
iv) dodecaedro regular ,
iii) octaedro regular,
v) icosaedro
regular
http://www.uff.br/cdme/platonicos/platonicos-html/solidos-platonicos-br.html
POLIEDROS REGULARES
Exercício:
Preencha a tabela abaixo:
Poliedro regular
V
A
tetraedro
4
6
cubo (hexaedro regular)
8
12
F
n-arestas
em cada
face
m-arestas
em cada
vértice
4 faces
3
3
6 faces
4
3
octaedro
8 faces
dodecaedro
12 faces
icosaedro
20 faces
CILINDRO
Definição:
Considere α e β dois planos paralelos,
um círculo Г contido em α e uma
reta s que corta α e β.
CILINDRO
Definição:
Considere α e β dois planos paralelos,
um círculo Г contido em α e uma
reta s que corta α e β.
Para cada ponto X de Г, trace uma
reta paralela a s e seja X’ tal ponto
de interseção com β.
Chama-se cilindro circular ou cilindro
a reunião de todos os segmentos XX’,
onde X pertence a Г(região circular).
CILINDRO
Elementos:
i) 2 bases: círculos congruentes situados em planos paralelos.
ii) geratrizes:
segmentos com uma das extremidades
em um ponto da circunferência de centro O e raio r e outra no ponto correspondente da circunferência de centro
O’ e raio r.
iii) O eixo do cilindro é a reta determinada pelos centros das
bases.
r é o raio da base.
a altura de um cilindro é a distância h entre os planos das bases.
CILINDRO
Superfícies:
Superfície lateral:
é a reunião das geratrizes.
Superfície total:
é a reunião da superfície lateral com os círculos das bases.
CILINDRO
Classificação:
Cilindro circular obliquo: se as geratrizes são obliquas aos planos
das bases.
Cilindro circular reto: se as geratrizes são perpendiculares aos
planos das bases.
Cilindro de revolução : é o cilindro circular reto e é gerado pela rotação de um retângulo em torno de um eixo, que contém um dos seus
lados.
CILINDRO
Seção Meridiana :
É a interseção do cilindro com um plano que contém a reta OO’,
denominada pelos centros das bases.
A seção meridiana de um cilindro obliquo é um paralelogramo.
(Faça um desenho que represente esta seção).
CILINDRO
Seção Meridiana :
É a interseção do cilindro com um plano que contém a reta OO’,
denominada pelos centros das bases.
A seção meridiana de um cilindro obliquo é um paralelogramo.
(Faça um desenho que represente esta seção).
A seção meridiana de um cilindro
reto é um retângulo. Veja figura
ao lado .
CILINDRO
Cilindro equilátero:
É um cilindro cuja seção meridiana é um quadrado.
Portanto
g = h =2r
CILINDRO
Área Lateral de um Cilindro circular reto
A área lateral de um cilindro circular reto ou cilindro de revolução
é equivalente a um retângulo de dimensões 2  r (comprimento
da circunferência da base) e h (altura do cilindro)
Ou seja, a área lateral do cilindro circular reto é:
2  r  h
CILINDRO
Área Total de um Cilindro circular reto
É a soma da área lateral Al com as áreas das duas bases
B    r2
A área total do cilindro circular reto é:
At  2  r (h  r )
CILINDRO
Volume do Cilindro
O volume de um Cilindro é o produto da área da base pela medida da
altura.
Prova: Considere
- um cilindro S1 de altura h e área da base B1  B e um prisma S 2
de altura h e área da base B2  B .
CILINDRO
Volume do Cilindro
-
-
Suponha que os dois sólidos têm as bases num mesmo plano, α e
estão num dos semi-espaços determinados por α.
Qualquer plano β paralelo a α, que secciona o cilindro também
secciona o prisma e as seções têm áreas iguais.
B1'  B1 , B2'  B2 , B1  B2  B  B1'  B2'
CILINDRO
Volume do Cilindro
Então, pelo Princípio de Cavalieri, o cilindro e o prisma têm volumes
iguais.
VCilindro  VPrisma
Como VPrisma  B2  h  B  h  VCilindro  B  h 
Se B    r 2
 VCilindro    r 2  h
V  B h
CILINDRO
Volume do Cilindro
Exercício:
Um tubo de tinta de uma caneta esferográfica tem 2 mm de diâmetro
e 10 cm de comprimento. Vamos supor que você gasta 2 mm3 de tinta
por dia. Nessas condições a tinta de sua caneta esferográfica durará
quantos dias?
CILINDRO
Volume do Cilindro
Exercício:
Um tubo de tinta de uma caneta esferográfica tem 2 mm de diâmetro
e 10 cm de comprimento. Vamos supor que você gasta 2 mm3 de tinta
por dia. Nessas condições a tinta de sua caneta esferográfica durará
quantos dias?
Solução: Tubo de tinta é um cilindro cujo diâmetro da base é 2 mm e
altura 10 cm = 100 mm.
V   .12.100  100 mm3
O volume de tinta é:
3
Em um dia, gasto 2 mm de tinta, então:
1 dia x
2 mm 3
- 100 mm 3
 x
1.100
 50 dias
2
CONE
Definição:
Considere um círculo Г contido no plano α e seja V um ponto fora do
plano α. Para cada ponto X pertencente a α, trace o segmento VX.
Chama-se cone circular ou cone à reunião dos segmentos VX.
CONE
Elementos
uma base : círculo de centro O e raio r,
vértice: o ponto V.
geratrizes : segmentos ligando o vértice V a um ponto da circunferência da base.
A altura de um cone é a distância entre o
Vértice e o plano da base.
Superfície lateral: reunião das geratrizes.
Superfície total : reunião da superfície
lateral com o círculo da base.
CONE
Classificação
Pela posição de VO em relação ao plano da base.
Cone circular obliquo – Se VO é obliqua ao plano da base.
Cone circular reto ou cone de revolução - se VO é perpendicular ao
plano da base.
CONE
Seção meridiana
Interseção do cone com um plano que contém VO.
A seção meridiana de um cone circular reto ou cone de revolução é um
triângulo isósceles.
CONE
Cone equilátero
Cone cuja seção meridiana é um triângulo equilátero.
CONE
Áreas Lateral e Total de um cone circular reto
A superfície lateral de um cone circular reto (cone de revolução) de raio
da base r e geratriz g é equivalente a um setor circular de raio g e
comprimento do arco 2  r.
Asetor
Sendo θ o ângulo do setor, temos que :

2 r
360 r
rad ou  
graus
g
g
2 r.g   g 2


2
2
CONE
Áreas Lateral e Total de um cone circular reto
Área lateral do cone:
Comprimento do arco
2  g
2  r
área do setor
________
________
  g2
Al
Al   r g
2 r   g 2
 Al 
2 g
CONE
Áreas Lateral e Total de um cone circular reto
Área lateral do cone:
Comprimento do arco
2  g
2  r
área do setor
________
________
  g2
Al
Al   r g
Ou ainda, a área do setor circular é
Asetor 
2 r.g
  r g  Al
2
2 r   g 2
 Al 
2 g
CONE
Áreas Lateral e Total de um cone circular reto
Área total :
At  Al  B
onde a área da base é
B   r2
Logo
At   r g   r 2
 At   r ( g  r )
CONE
O volume do Cone
O volume do cone é um terço do produto da área da base pela medida
da altura.
2
B


r
, temos que V  1  r 2 h,
Se
3
Exercício:
Use o Princípio de Cavalieri para demonstrar o resultado acima.
CONE
O volume do Cone
Exemplo: Na base de um cone, cujo volume é igual a 144 m , está
inscrito um hexágono regular de área 54 3 m2 . Determine a área
total desse cone.
Solução:
3
CONE
O volume do Cone
Exemplo: Na base de um cone, cujo volume é igual a 144 m , está
inscrito um hexágono regular de área 54 3 m2 . Determine a área
total desse cone.
Solução: V  144
6 R2 3
A área do hexágono é :
 54 3  R2  36  R  6
4
3
V  144 
h2  R2  g 2
 R2 h
3
62 h
 144 
 h  12
3
 g 6 5
AT   R2   Rg  36 (1  5)m2
ESFERA
Definição
Considere um ponto O e r um número real positivo. Denominamos
esfera de centro O e raio r o conjunto dos pontos P do espaço cuja
distância OP é menor ou igual a r.
Superfície da esfera de raio r e centro O:
ao conjunto dos pontos do espaço cuja distância
OP seja igual a r.
OBS:
A superfície da esfera é também superfície de revolução gerada pela
rotação de uma semicircunferência com extremidades no eixo.
ESFERA
Seção plana de uma esfera:
ESFERA
Seção plana de uma esfera: é um círculo.
Se o plano secante passa pelo centro da esfera, temos como
seção um círculo máximo da esfera.
Se r é o raio da esfera,d a distância do
plano secante ao centro e s=O’A é o
raio da seção, vale :
s2  r 2  d 2
ESFERA
Área e Volume
A área da superfície de uma esfera de raio r é
A  4 r 2
Exercício: Deduza a fórmula acima. (pagina 231)
O volume da esfera de raio r é:
4
V   r3
3
´
ESFERA
Área e Volume
Exemplo: Um plano secciona uma esfera, determinando um círculo de
raio igual à distância do plano ao centro da esfera. Sendo 36 m2
a área deste círculo, calcule o volume da esfera.
Solução:
ESFERA
Área e Volume
Exemplo: Um plano secciona uma esfera, determinando um círculo de
raio igual à distância do plano ao centro da esfera. Sendo 36 m2
a área deste círculo, calcule o volume da esfera.
Solução:
No triângulo O´AO,
r 2  r 2  R2  R  r 2
Por hipótese,
 r 2  36  r  6
4
V   R3  576 2  m3
3
ESFERA
Área e Volume
Exemplo: Um copo de chopp é um cone (oco). Se uma pessoa bebe
desde que o copo está cheio até o nível de bebida ficar exatamente na
metade da altura do copo, que fração do volume total é consumida?
Solução:
ESFERA
Área e Volume
Exemplo: Um copo de chopp é um cone (oco). Se uma pessoa bebe
desde que o copo está cheio até o nível de bebida ficar exatamente na
metade da altura do copo, que fração do volume total é consumida?
Solução:
R
h

h
x
2
V
R
x
2

R3h
3
2
Vmetade
R h
  
2
2  2 R h



3
24
Vconsumido 
R2h
3
R2h
7R2h


24
24

7R2 h
2
7

R
h
3
7
24 


R2 h
24
R2 h 8
3
POLIEDRO CONVEXO, CONE, CILINDRO E ESFERA
Área e Volume
Exercícios: Considere o cubo de vértices A,B,C,...F,G e H representado
2
m2 , calcule o
na figura. Sabendo que a área do triângulo DEC é
2
volume da pirâmide cujos vértices são D, E, G e C.
POLIEDRO CONVEXO, CONE, CILINDRO E ESFERA
Área e Volume
Exercícios: Considere o cubo de vértices A,B,C,...F,G e H representado
2
m2 , calcule o
na figura. Sabendo que a área do triângulo DEC é
2
volume da pirâmide cujos vértices são D, E, G e C.
Resp : V 
1
m3
6
POLIEDRO CONVEXO, CONE, CILINDRO E ESFERA
Área e Volume
Exercícios:
Livro texto, capítulos: Poliedro convexo, cilindro, cone e esfera.