Apresentação do PowerPoint - A Física tá complicada?

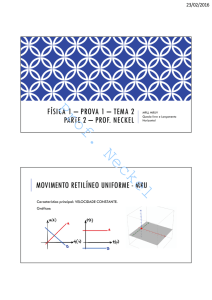
v(t) =
CURSO: Engenharia Civil
DISCIPLINA: Mecânica da Partícula
PROFº: MSc. Demetrius Leão
1
ACOMPANHE A DISCIPLINA PELA INTERNET
• Página com as aulas e listas de exercícios:
“A Física tá complicada?”
http://simplephysicsbr.wordpress.com/
• E-mail: [email protected]
2
OBJETIVOS DESSA AULA:
• Conhecer as características principais do MRUV
(deslocamentos, velocidades, aceleração).
• Diferenciar o MRUV do MRU.
• Conhecer as funções desse movimento.
• Diferenciar velocidade de aceleração.
3
O astronauta David Scott, comandante da missão Apollo 15 (1971), realizou um
experimento de queda livre em sua última caminhada lunar. Segurando uma
pena de falcão na mão esquerda e um martelo de alumínio na mão direita, o
astronauta deixou-os cair de uma altura aproximada de 1,6 m (pouco abaixo
dos seus ombros). E os dois tocaram o solo lunar juntos!
5
O que eu devo relembrar?
• Funções do segundo grau e seus gráficos.
f(x)= ax²+bx+c
6
O MOVIMENTO RETILÍNEO UNIFORMEMENTE VARIADO
(MRUV)
No movimento retilíneo uniforme (MRU), a velocidade não
varia e a aceleração é nula. A partir de agora vamos
revisar movimentos cuja velocidade varia de maneira
uniforme, o que significa que a aceleração do movimento é
constante.
Qual a
aceleração
desse
movimento?
7
Características do MRUV
Como a velocidade da bola aumenta, ela percorre
distâncias cada vez maiores em intervalos de
tempo iguais.
A distância entre duas posições sucessivas aumenta com
o passar do tempo.
8
EQUAÇÕES DO MRUV
• Função horária dos espaços.
• Função horária da velocidade.
COMO “LER” UMA EQUAÇÃO DE VELOCIDADE?
• v(t) = 5 + 2t
– > v0= 5m/s a=2 m/s²
• v(t) = 2t -5
---> v0= -5m/s a=2 m/s²
• v(t) = 5t
---> v0= 0 m/s a=5 m/s²
10
COMO “LER” UMA EQUAÇÃO DE POSIÇÃO?
• s(t) = 5 + 2t + 3t²
– > s0= 5m v0= 2m/s
a=6 m/s²
• s(t) = - t²+ 2t + 5
---> s0= 5m v0= 2m/s
a=-2 m/s²
• s(t) = - t²
---> s0= 0
v0= 0m/s
a=-2 m/s²
11
COMO “LER” UMA EQUAÇÃO DE POSIÇÃO?
• s(t) = 5t²
– > s0= 0
v0= 0
a=10 m/s²
• s(t) = 2t + 5
---> Não se trata de um MRUV, mas sim de um MRU
12
EXEMPLO 1
(VUNESP) No jogo do Brasil contra a Noruega, o tira-teima mostrou que o atacante
brasileiro Roberto Carlos chutou a bola diretamente contra o goleiro do time
adversário. A bola atingiu o goleiro com velocidade de 108 km/h e este conseguiu
imobilizá-la em 0,1 s, com um movimento de recuo dos braços. O módulo da
aceleração média da bola durante a ação do goleiro foi, em m/s2, igual a:
a) 3.000.
b) 1.080.
c) 300.
d) 108.
e) 30.
RESPOSTA: C
EXEMPLO 2
O movimento de uma partícula é descrita pela função s(t) = 1200 - 70t + t² com as unidade
no SI. Para uma trajetória retilínea, determine:
a) a posição inicial
1200 m
b) a velocidade em t = 0
resp: - 70 m/s
c) a sua aceleração
(resp: 2 m/s2); a/2 = 1→ a =2 m/s2
d) a velocidade em t = 30s (resp:- 10 m/s);
v = vo + v.t
v = - 70 +2t
v = -70 + 2.30
v = - 70 + 60
v = - 10 m/s
EXEMPLO 2
O movimento de uma partícula é descrita pela função s(t) = 1200 - 70t +
t² com as unidade no SI. Para uma trajetória retilínea, determine:
e) o instante que o movimento inverte o sentido;
v = - 70 + 2t
0 = - 70 +2t
70 =2t
t = 70/2
t = 35 s
f) o instante em que v = 33m/s
v = - 70 +2t
33 = - 70 +2t
33 + 70 = 2t
103 =2t
t = 103/2
t = 51,5 s
Equação de Torricelli
Em certas situações do MRUV, podemos determinar parâmetros do
movimento, como velocidades iniciais ou finais, distância percorrida ou
aceleração, sem empregar medidas de tempo. Para isso, eliminamos o
tempo na função horária da posição no MRUV:
(Equação de Torricelli)
O MOVIMENTO RETILÍNEO UNIFORMEMENTE VARIADO (MRUV)
EXEMPLO 3
(UEL-PR) Um motorista está dirigindo um automóvel a uma
velocidade de 54 km/h. Ao ver o sinal vermelho, pisa no freio. A
aceleração máxima para que o automóvel não derrape tem módulo
igual a 5 m/s2. Qual a menor distância que o automóvel irá
percorrer, sem derrapar e até parar, a partir do instante em que o
motorista aciona o freio?
a) 3,0 m
b) 10,8 m
c) 291,6 m
d) 22,5 m
e) 5,4 m
RESPOSTA: D
17
GRÁFICOS
18
19
III. Gráficos s X t (MRU)
O MOVIMENTO RETILÍNEO UNIFORME (MRU)
20
III. Gráficos v X t (MRU)
21
IV. Deslocamento a partir do gráfico v X t
A área da figura formada pelo gráfico v x t fornece o deslocamento do objeto entre os instantes t1 e t2.
22
23
IV. Deslocamento a partir do gráfico v X t
O deslocamento corresponde numericamente à área abaixo do gráfico.
24
Função horária da posição e seus gráficos no MRUV
O MOVIMENTO RETILÍNEO UNIFORMEMENTE VARIADO (MRUV)
26
EXEMPLO 4
(UCS-RS) Um móvel descreve um movimento retilíneo, com velocidade variando
com o tempo, conforme o gráfico. Pode-se afirmar então que:
a) a aceleração do móvel é nula.
b) a velocidade do móvel é constante.
c) a aceleração do móvel é constante e
vale 5 m/s2.
d) o móvel percorre 60 m em 2 s.
e) a velocidade média do móvel de 0 a
2 s vale 5 m/s.
RESPOSTA: C
EXEMPLO 5
(UFJF-MG) Dois carros estão se movendo em uma rodovia, em
pistas distintas. No instante t = 0 s, a posição do carro 1 é s = 75 m
e a do carro 2 é s = 50 m. O gráfico da velocidade em função do
tempo para cada carro é dado a seguir.
01
a) A partir do gráfico, encontre a
aceleração de cada carro.
b) Escreva a equação horária para
cada carro.
c) Descreva, a partir da análise do
gráfico, o que ocorre no instante t=5 s
RESPOSTA:
28
29