Integral Definida

www.matematiques.com.br
Cálculo 2
6ª Lista de Exercícios – Integral Definida
Integral Definida
O matemático grego Arquimedes (287 – 212 A.C.) utilizou o denominado método de exaustão para determinar a
quadratura da parábola. O método, cujo desenvolvimento foi creditado a Eudoxo (cerca de 370 A.C.), consiste em
exaurir ou esgotar a região, cuja área se quer determinar, por meio de outras áreas já conhecidas.
Vejamos agora como definir e calcular a área de uma região limitada por uma função f, contínua em um intervalo
[a,b].
A
B
A
B
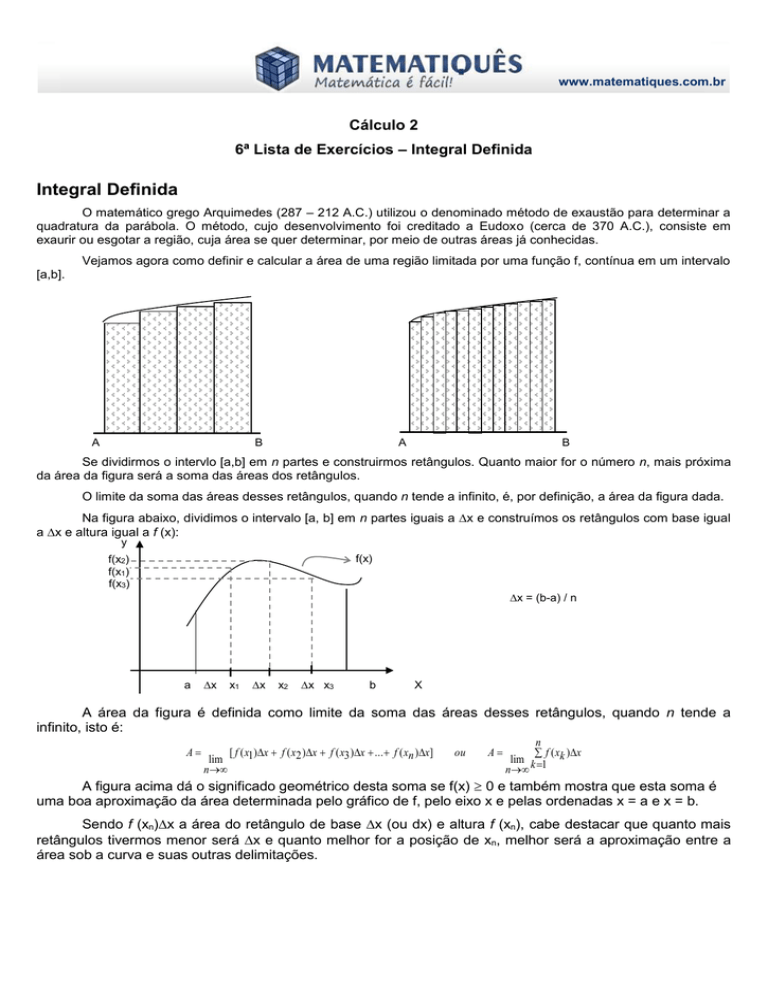
Se dividirmos o intervlo [a,b] em n partes e construirmos retângulos. Quanto maior for o número n, mais próxima
da área da figura será a soma das áreas dos retângulos.
O limite da soma das áreas desses retângulos, quando n tende a infinito, é, por definição, a área da figura dada.
Na figura abaixo, dividimos o intervalo [a, b] em n partes iguais a x e construímos os retângulos com base igual
a x e altura igual a f (x):
y
f(x)
f(x2)
f(x1)
f(x3)
x = (b-a) / n
a
x
x1
x
x2
x x3
b
X
A área da figura é definida como limite da soma das áreas desses retângulos, quando n tende a
infinito, isto é:
A
lim
n 
[ f ( x1)x  f ( x2 )x  f ( x3 )x  ...  f ( xn )x]
ou
A
n
 f ( x )x
lim k 1 k
n 
A figura acima dá o significado geométrico desta soma se f(x)  0 e também mostra que esta soma é
uma boa aproximação da área determinada pelo gráfico de f, pelo eixo x e pelas ordenadas x = a e x = b.
Sendo f (xn)x a área do retângulo de base x (ou dx) e altura f (xn), cabe destacar que quanto mais
retângulos tivermos menor será x e quanto melhor for a posição de xn, melhor será a aproximação entre a
área sob a curva e suas outras delimitações.
www.matematiques.com.br
Exemplo:
y
y






















x
x












































n=2
n=4





y


y
























x















x

n=8









n = 40



Definição: A integral definida de f, desde a até b é o
n
 f ( x k )x
lim
,
n k 1
Símbolo :
n
b f ( x)dx 
( fxk )x

a
lim
n k 1
 Teorema Fundamental do Cálculo
Consideremos f(x) uma função definida num intervalo [a, b]. Suponhamos que exista uma função F(x),
definida e derivável nesse intervalo, tal que F’(x) = f(x), para todo x  [a, b]. Então, temos:

b
a
f (x)dx  F(x)  F(b)  F(a ) , onde F é uma integral indefinida de f.
b
a
Exercício–Exemplo : Calcular
1
x
0
2
dx
x3
Uma primitiva de f(x) = x é, como vimos, F(x) =
. Assim:
3
2
1
x3 
1 0 1
x
dx

    
0
 3 0  3 3 3
1
2
www.matematiques.com.br
 CÁLCULO DE ÁREAS
Com a integral definida podemos calcular áreas. Isso ficou mostrado pelas considerações feitas
anteriormente. Podemos então considerar 4 casos do uso da integral definida para calcular áreas :
1.º caso
A área está toda acima do eixo x ou seja f(x)  0 para todo x  [a, b] , então
b
A   f (x)dx
a
y
F : [a, b]  R , e f(x)  0  x  [a, b].
X
a
2.º caso
b
A área está toda abaixo do eixo x ou seja f(x)  0 para todo x  [a, b] , então
A

b
a
f ( x )dx
y
a
F : [a, b]  R, e f(x)  0  x  [a, b].
b
X
Neste caso, a área assinalada será calculada por:

b
a
3.º caso
 f ( x )dx
ou

b
a
f ( x )dx
ou

a
b
f ( x )dx
A área está abaixo e acima do eixo x, ou seja f(x)  0 e f(x)  0 para todo x  [a, b]. Então se calcula a(s)
raiz(es) de f(x) e se estas estão no interior do intervalo de integração teremos:
y

x1
a
f ( x)dx  x f ( x)dx .
b
1
X1 é a raiz da f(x) neste exemplo.
a
X
x1
b
F : [a, b]  R, e f(x) assume valores positivos,
negativos e nulos para todo x  [a, b].
4.º caso
A região cuja área queremos calcular, está situada entre duas curvas.
y
f(x)
g(x)
X
a
b
Como se vê, f(x)  g(x),  x  [a, b], logo f(x) – g(x)  0.
Portanto, a função F(x) = f(x) – g(x) encaixa–se no 1.º caso:
A  a ( f ( x)  g ( x) ) dx
b
www.matematiques.com.br
Exercícios:
1) Calcule as integrais definidas abaixo:
a)

2
6x 4 dx
1
2
b)
 (5x
c)

d)
 x3

2

dx

2
x

7
x

1
 2  3

e)

f)
 (6x  1)dx
g)

1
2
0
4
 8x 3 )dx
sen( 2x)dx
2
4
0
( 2x  1) dx
2
1
2
1
x(1  x 3 )dx
R:
198
5
R:
 37
24
R:0
R : - 6,667
R : 8,667
R:8
R:
81
10
2) Calcular a área determinada pelas curvas de equações y = x2 – 3x – 4 ; y = 0 ; x = 0 e x = 5.
R:
73
u.a.
6
3) Calcular a área compreendida entre a curva y = x2, o eixo x, e as ordenadas correspondentes às abcissas
x = 0 e x = 2.
R:
8
u.a.
3
4) Calcule a área compreendida entre os gráficos das funções y 
R:
x ; y = 0 e a reta x = 4
16
u.a.
3
5) Calcule a área compreendida entre a curva y = 5x + 1, o eixo x e as retas x = – 3
R: 23,2 u. a.
6) Calcular a área entre as curvas y = – x2 + 4 e y = 1 no intervalo [–1, 1].
R:
16
u.a.
3
7) Calcular a área entre as curvas y = x2 – 4 e y = x – 3 .
R: 1,86 u.a.
Integral Definida: http://wwwp.fc.unesp.br/~arbalbo/arquivos/integraldefinida.pdf
e x = 1.
www.matematiques.com.br
EXERCÍCIOS PROPOSTOS
Calcule a integral definida usando Geometria Elementar:
1.
2.
3.
4. 1.
Use o TFC para calcular a integral definida
5.
7.
6.
dx
8.
dx
9.
dx
10.
dx
11.
dx
12.
dx
14.
dx
13.
dx
15.
dx
16.
dx
Calcule a área sob o gráfico de f .
17. y = -x2 + 10x - 24, 4 ≤ x ≤ 6
19. y = -x2,
0≤x≤2
21. y = 2x2 – 11x + 5, 0 ≤ x ≤ 5
18. y = x2 - 3, 0 ≤ x ≤ 3
20. y = x4, - 2 ≤ x ≤ 1
22. y = x, - 2 ≤ x ≤ 2