Trabalho e Energia Cinética

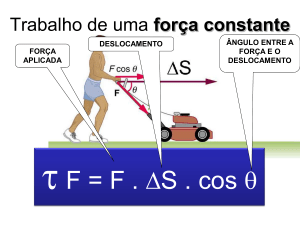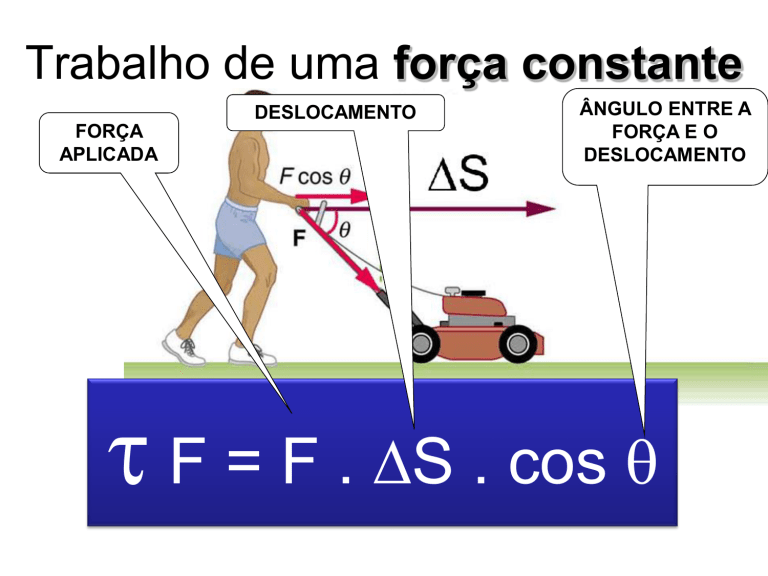
Trabalho de uma força constante
FORÇA
APLICADA
DESLOCAMENTO
ÂNGULO ENTRE A
FORÇA E O
DESLOCAMENTO
 F = F . S . cos 
Trabalho de uma força
QUALQUER
POTÊNCIA (Pot)
Mede a velocidade com que
um trabalho é realizado.
τ
F
Pot 
 F.v. cos 
Trabalho realizado
pela força
t
Tempo gasto para
realizar esse
trabalho
Trabalho e Energia Cinética
O conceito de energia é bastante
novo na ciência, tendo se firmado
há aproximadamente cem anos.
Trabalho e Energia Cinética
Partindo da Equação de Torriceli
V
2
2
 V 0  2.a.S
Podemos escrever (...passando o V0 “p’ra” lá...)
V V 0
2
2
 2.a.S
2
Dividindo cada termo por dois (2), obtemos.
2
Trabalho e Energia Cinética
MULTIPLICANDO PELA MASSA DO CORPO
2
m .V
2
m .V 0

2
2
 m .a.S
Trabalho e Energia Cinética
2
m .V
2
m .V 0

2
2
 mF. a.S
FORÇA
RESULTANTE
2
2
m
.
V
m
.
V
0


m.a. S 
2
2
.
FORÇA

Ec

Ec
F
0
F
F  Ec  Ec
f
F

0
Ec
Trabalho e Energia
são grandezas
“equivalentes”.
F

Ec
O trabalho mede a
variação de energia
de um sistema
F

Ec
Trabalho Resistente
(consome Energia)
Ec  0
Trabalho MOTOR
(fornece Energia)
Ec > 0
Apesar de ser um conceito bastante utilizado, a
definição de energia não é consensual.
Energia está relacionada com a possibilidade
de mover “alguma coisa” ou alterar
propriedades da matéria.
No SI
Joule (J)
Usuais
quilowatt.hora (kWh)
1kWh = 3,6 x 106 J
Caloria
1cal ~ 4,18J ~ 4,2J ~4J
ENERGIA MECÂNICA
CINÉTICA, associada
ao movimento
ENERGIA MECÂNICA
CINÉTICA, associada
ao movimento
Depende:
•Da massa (m)
m.v
E 
2
c
•Da velocidade (v)
F
RESULTANTE
= Ec
2
Ex 11
F (N)
50
30
F
2
10
d (m)
exercícios
ENERGIA MECÂNICA
POTENCIAL
(“armazenada”),
associada à
possibilidade de
produzir
movimento
ENERGIA POTENCIAL
GRAVITACIONAL
(associada à distância
que um corpo está de
uma superfície)

g
h
ENERGIA POTENCIALGRAVITACIONAL
M
Depende de:
• Massa (m);
• “Altura” (h);
• Gravidade (g).

m
.
g
.
h
EG
FG I – O C V
Exemplo

Força Peso
•O trabalho realizado pelo peso do corpo depende apenas das suas
posições inicial e final (não depende do percurso) – Força Conservativa
situação final:
situação inicial:
hf
ho
MRCP
 peso  E g
DF – UM
forças CONSERVATIVAS
São forças cujo trabalho
realizado não depende da
trajetória descrita entre a
posição inicial e a posição
final.
forças CONSERVATIVAS
 FA, B = EA - EB
ENERGIA POTENCIAL
ELÁSTICA (associada a materiais
flexíveis – molas, elásticos, borrachas, etc)
ENERGIA POTENCIAL ELÁSTICA
Depende de:
Material (k);
Deformação (x).
.x
k
E  2
El
2
LIÇÃO DE CASA
Apostila exs. 12 a 14
Livro
Para continuar aprendendo
pgs. 394...
3e6