Lista_revisao_simulado2016 - Instituto Montessori

Instituto Montessori - Ponte Nova
Atividade de Geometria – 1º ano – 1º trimestre
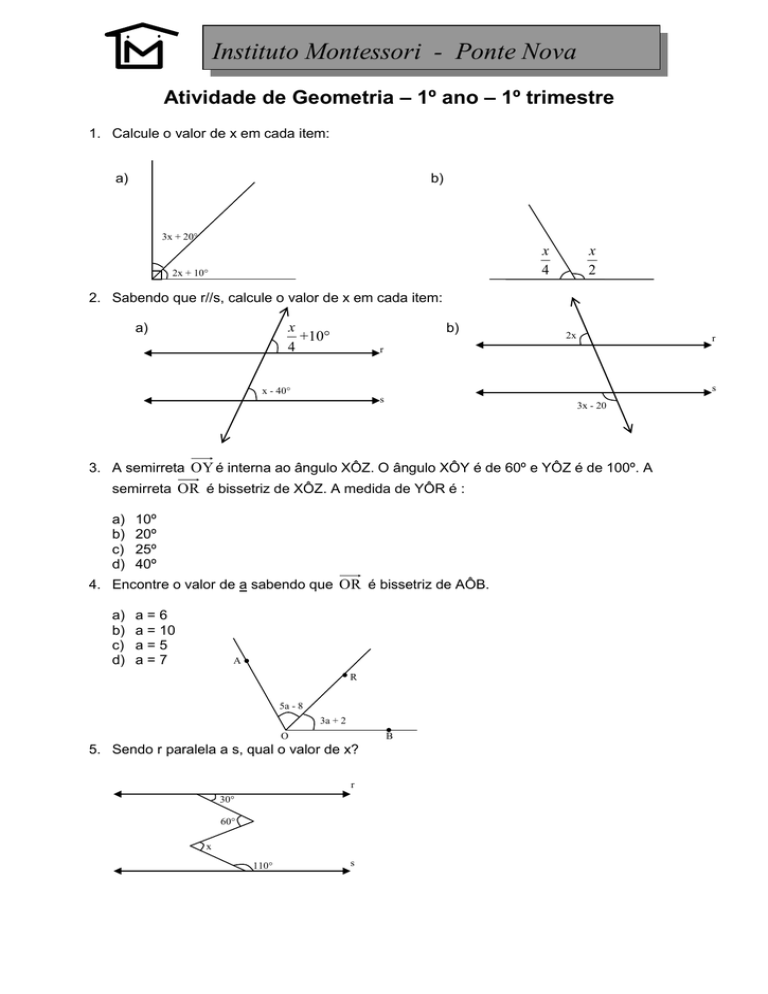
1. Calcule o valor de x em cada item:
a)
b)
3x + 20°
x
4
2x + 10°
x
2
2. Sabendo que r//s, calcule o valor de x em cada item:
x
+10°
4
a)
b)
2x
r
r
s
x - 40°
s
3x - 20
3. A semirreta OY é interna ao ângulo XÔZ. O ângulo XÔY é de 60º e YÔZ é de 100º. A
semirreta OR é bissetriz de XÔZ. A medida de YÔR é :
a)
b)
c)
d)
10º
20º
25º
40º
4. Encontre o valor de a sabendo que OR é bissetriz de AÔB.
a)
b)
c)
d)
a=6
a = 10
a=5
a=7
A
R
5a - 8
3a + 2
B
O
5. Sendo r paralela a s, qual o valor de x?
r
30°
60°
x
110°
s
6. As bissetrizes de dois ângulos adjacentes formam um ângulo de 60°. Se um deles mede 40°, qual
é a medida do outro?
7.
Calcule os valores das letras indicadas nas figuras:
a)
b)
x
3x + 10°
y
x + 50°
z
95°
45°
y
8. Duas retas paralelas cortadas por uma transversal determinam ângulos colaterais externos tais que
um deles é o triplo do outro. Quanto mede o menor dos ângulos?
a)
b)
c)
d)
30º
45º
60º
80º
9. Duas retas formam com uma transversal ângulos correspondentes expressos em graus por 10x –
11º e 49º - 5x. Determine x para que essas retas sejam paralelas.
a)
b)
c)
d)
3
2
4
5
10. Observe, na figura, três quadrados identificados por I, II e III, que foram construídos sobre os
lados de um triângulo retângulo, Se a área do quadrado I é 36 cm2 e a área do quadrado III é
64 cm2, determine:
a) a área do quadrado II
b) a medida do lado do quadrado III.
II
I
III
11. No triângulo ABC, retângulo em Â, temos: AC = 8 cm e BC = 10 cm. Sendo AD perpendicular
a BC , qual é o comprimento do segmento AD
12. Um triângulo retângulo tem os catetos medindo 6 m e 8m. Os valores de x, y e z são,
respectivamente:
a) 5, 6 e 4
b) 2, 4 e 3
8
10
,2 e
c)
3
3
18 32
24
,
e
d)
5 5
5
6
8
z
x
y
13. Calcule o valor de x na figura.
14. (PUC MG) Um desfile de moda é feito sobre um palco retangular de comprimento MN  24m e
de largura AM  6m . Certa modelo sai do ponto A, percorre a poligonal ABCDE e termina de
desfilar no ponto E. Considerando-se que MB BD  DN e que o triângulo BCD é isósceles,
BC  CD  5m , pode-se estimar que a distância, em metros, percorrida por essa modelo, durante
seu desfile, é?
15. Uma antena de TV é colocada sobre um bloco de concreto. Esse bloco tem 1 m de altura. Em
um certo instante, a antena projeta uma sombra de 6 m, enquanto o bloco projeta uma sombra
de 1,5 m. Nessas condições, qual é a altura da antena?
16. Um homem de 1,80 m de altura projeta uma sombra de 2,70 m de comprimento no mesmo
instante em que uma árvore projeta uma sombra de 9 m de comprimento. Qual é a altura da
árvore?
17. Uma ripa de madeira de 1,5 m de altura, quando colocada verticalmente em relação ao solo,
projeta uma sombra de 0,5 m. No mesmo instante, uma torre projeta uma sombra de 15 m.
Calcule a altura da torre.
18. Na figura abaixo, AB // ED . Nessas condições, determine os valores de x e y.
19. As bases de dois triângulos isósceles semelhantes medem, respectivamente, 8 cm e 4 cm. A
medida de cada lado congruente do primeiro triângulo é 10 cm. Nessas condições, calcule:
a) a medida de cada lado congruente do segundo triângulo.
b) os perímetros dos triângulos.
c) a razão de semelhança do primeiro para o segundo triângulo.
20. O incentro de um triângulo é ponto de encontro das:
a)
b)
c)
d)
Bissetrizes;
Medianas;
Alturas;
Mediatrizes.