Mediana, bissetriz e altura de um triângulo

E.E”Prof.José de Almeida Pinheiro JR”
Disciplina: Matemática
a
3º. EM – Prof . Valéria Rojas Assunto: Mediana, Bissetriz e Altura de um triângulo
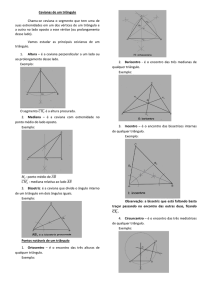
Mediana, bissetriz e altura de um triângulo
Sabemos que os elementos básicos
de um triângulo são: os vértices,
os lados e os ângulos, mas não são
os únicos. Em um triângulo
identificamos outros elementos,
como mediana, bissetriz e altura.
Vértices, lados e ângulos.
Figura 01:
Vértices: A, B e C
Lados: AB, BC e AC
Ângulos: A, B e C
Mediana
Mediana é um segmento que divide as bases do triângulo em duas partes
iguais. Dessa forma temos que mediana é um segmento de reta com origem
em um dos vértices do triângulo e extremidade no ponto médio do lado oposto
ao vértice. Observe a figura:
Figura 02:
A, B e C são os vértices do
ΔABC.
M ponto médio da base BC,
dessa forma BM = MC.
AM segmento de reta com
extremidades no vértice A e no
ponto médio M, portanto, nesse
exemplo podemos dizer que o
segmento AM é a mediana do
ΔABC.
Bissetriz
Bissetriz também é um segmento de reta com origem em um dos vértices do
triângulo com a outra extremidade no lado oposto a esse vértice. Sendo que ela
divide ao meio o ângulo correspondente ao vértice. Veja o exemplo:
Que o Senhor seja eternamente louvado
Página 1
E.E”Prof.José de Almeida Pinheiro JR”
Disciplina: Matemática
a
3º. EM – Prof . Valéria Rojas Assunto: Mediana, Bissetriz e Altura de um triângulo
AS é um segmento de reta que
dividiu o ângulo  em duas partes
iguais.
Figura 03:
Altura
Encontramos a medida da altura de um triângulo através de um segmento de
reta com origem em um dos vértices e perpendicular (forma um ângulo de 90º)
ao
lado
oposto.
Altura no triângulo acutângulo
O segmento AH tem origem no vértice A
e é perpendicular ao lado BC, portanto,
AH é a altura do ΔABC.
Figura 04:
Altura no triângulo retângulo
Nesse triângulo, o segmento EF
representa a altura do ΔEFG, pois é
perpendicular ao lado FG.
Figura 05:
Que o Senhor seja eternamente louvado
Página 2
E.E”Prof.José de Almeida Pinheiro JR”
Disciplina: Matemática
a
3º. EM – Prof . Valéria Rojas Assunto: Mediana, Bissetriz e Altura de um triângulo
Altura no triângulo obtusângulo
A base RQ foi prolongada formando o
segmento RX. Do vértice P ao ponto x
formamos um segmento de reta
perpendicular a RX, dessa forma, PX é a
altura do ΔPQR.
Figura 06:
Que o Senhor seja eternamente louvado
Página 3