operações com radicais

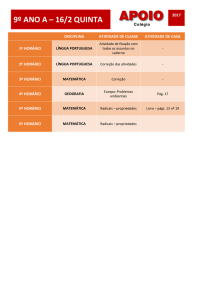
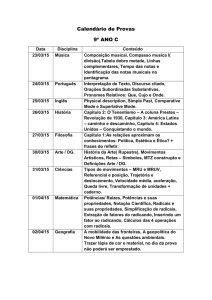
ESCOLA SECUNDÁRIA DE D. DINIS – Sto Tirso
Ficha de Trabalho nº 1 - OPERAÇÕES COM RADICAIS
1)Adição algébrica com radicais:
- Para efetuar a adição algébrica com radicais, simplificamos os radicais e reduzimos os
termos que têm radicais iguais ( radicais de mesmo índice e mesmo radicando),
somando algebricamente os fatores externos.
Exercícios:
Calcula:
49  16 
a)
b)
3
8  4 16 
c)  5 9  2 169 
d) 103 2  43 2  3 2 
e) 18  2 50 
2)Efetua:
a) 3 5  5  6 5 
b) 55 3  25 3  25 3  5 3 
c)  4  3 5  23 5  4 
d) 25 3  2 3  3 3  35 3 
e)
50  18  8 
g) 4 63  7 
f) 2 27  5 12 
h) 12  75  108 
1
3)Encontra o perímetro das figuras, cujas medidas de seus lados são dadas numa mesma
unidade de medida de comprimento.
a)
b)
8
2 3
32
3 3
18
2)Multiplicação com radicais:
- Para multiplicar radicais de mesmo índice, devemos conservar o índice e multiplicar
os radicandos, simplificando sempre que possível o resultado obtido. Para efetuar essa
operação utilizamos a propriedade:
n
a b  n a  n b
Exercícios:
1)Efetua as multiplicações:
5 3 6 
b)
c)
2 6 3 
d)
e)
5  1 5 
a)
3


2 8 
3
4 3 6 


f) 3 2  2 

2 3 
2)Calcula a área e o perímetro das figuras, cujas medidas indicadas são dadas numa
mesma unidade de medida de comprimento.
a)
2 2
b)
3
1,5
2
1,5
1 2
3 2
2
3) Divisão com radicais
- Para dividir radicais de mesmo índice, devemos conservar o índice e dividir os
radicandos, simplificando sempre que possível o resultado obtido.
Exercícios:
1)Efetua as divisões:
a) 12  3 
49
c)
25
50  2 
b)

d)
123 6

33 2
2)Calcula o valor das expressões:
a)
 18 
 
98  200  2 2  8



b) 10 27  10 3  10 3


c) 20 10  10 18  2 2
4) Potenciação com radicais
- Para elevar um radical a uma potência, conservamos o índice do radical e elevamos o
radicando à potência indicada.
Exercícios:
1)Calcule as potências:
a)
 15 
c)

2

7 3
 



b) 3 7

2

2
d) 3  7
2

2)Calcula o valor da expressão A  x 4  x 2  2 para x  3 .
3
5) Radiciação com radicais:
- Para extrair a raiz de um radical, devemos multiplicar os índices desses radicais e
conservar o radicando, simplificando o radical obtido, sempre que possível (
considerando o radicando um número real positivo e os índices números naturais nãonulos).
Exercícios:
1)Reduz a um único radical.
a)
c)
3
10 
b)
3
d)
2 
3 3
3 
6) Racionalização de fracções:
O denominador da fracção
é um número irracional, enquanto o denominador de
é um número racional. Diz-se que racionalizámos o denominador da primeira
fracção. Esta é a transformação que, por norma, se aplica a todos os resultados em
forma de fracção com denominador irracional.
Exemplos
4
Exercicios:
1) Calcula:
a)
√3+1
2√5
c) √8 +
b)
√32
√2
−
6
3√2−√7
2√2
3
Bom Trabalho!
A professora: Dora Freitas
5