Números Complexos e Geometria Analítica 2013

Colégio Modelo
Exercícios de Números Complexos e Geometria Analítica
Professor Diniz – site: www.diniz.webnode.com.br
Bom Estudo!
1) O quociente de (8 + i)/(2 - i) é igual a:
a) 1 + 2i
b) 2 + i
c) 2 + 2i
d) 2 + 3i
e) 3 + 2i
2) Sendo z = 5i + 3i2 - 2i3 + 4i27 e w = 2i12 - 3i15 , calcule Im(z).w + Im(w).z .
a) -3 + 18i
b) -3 + 10i
c) - 5 + 18i
d) - 5 + 10 i
e) -3 + 12i
3) O valor da expressão y = i + i2 + i3 + ... + i1001 é:
a) i²
b) i
c) i³
d) i² + 1
e) i +1
4) Para que o produto (a + i).(3 - 2i) seja real, a deve ser:
a) 2/3
b) 4/3
c) 3/2
d) 3/4
e) 3/5
5) Seja z = 1 + i , onde i é a unidade imaginária. Podemos afirmar que z8 é igual a:
a) 16
b) 161
c) 32
d) 32i
e) 32 + 16i
6) Se o número complexo z = 1 – i é uma das raízes da equação x10 + a = 0 , então calcule o valor de a
a) 16i
b) 32i
c) 40i
d) 48i
e) 60i
7) (1 + i)15 é igual a:
a) 64(1 + i)
b) 128(1 – i)
c) 128(–1 – i)
d) 256(–1 + i)
e) 256(1 + i)
8) Dados os números complexos z1= a + bi e z2 = 1 2i. Como z1.z2 = 15, então z1 + z2 é igual a:
a) 8
b) 4
c) 4+4i
d) 6+i
e) 8  2i
9) O número complexo z, tal que 5z + 𝒛
̅ = 12 + 16i, é igual a:
a) – 2 + 2i
b) 2 + 4i
c) 2 – 3i
d) 3 + i
e) 1 + 2i
10) (UEFS) Se m - 1 + ni = (3 + i).(1 + 3i), então m e n são respectivamente:
a) 1 e 10
b) 5 e 10
c) 7 e 9
d) 5 e 9
e) 0 e -9
11) (Unitau) O módulo de z = 1 / i36 é:
a) 3.
b) 1.
c) 2
d) 1/36.
e) 36.
12) Quais são os possíveis valores de c para que os pontos (c , 3), (2 , c) e (14, -3) sejam colineares?
13) Qual é o valor de p para o qual os pontos (3p, 2p), (4, 1) e (2, 3) são colineares?
(A) -1
(B) 0
(C) 1
(D) 2
(E) 3
14) Multiplicando-se o número complexo z = 2 + 2i pela unidade imaginária i, obtém-se um número complexo cuja
representação, no plano, correspondente a um ponto PERTENCENTE À RETA de equação.
a) y = -x
b) y = - 2x + 2
c) y = x
d) y = -2x
e) y = 2x
15) Seja o número complexo z = 1 + i. O ARGUMENTO PRINCIPAL de z² é:
a) 30º
b) 45º
c) 0º
d) 90º
e)120º
3 e faça o que se pede.
16) Considere o número complexo 1 + i
A) Determine seu MÓDULO E ARGUMENTO PRINCIPAL.
B) Coloque-o na FORMA TRIGONOMÉTRICA.
C) Faça a representação GRÁFICA.
17) ESCREVA o número
5  5i
na forma polar.
2  2i
18) O gráfico seguinte representa uma função f, tal que f : IR  IR . A LEI que REPRESENTA a função f é:
A)
B)
C)
D)
E)
f (x) = 2x + 3
f (x) = - 2x – 3
f (x) = -2x + 3
f (x) = x + 3
f (x) = -1,5x + 3
19) Sabendo-se que a inclinação da reta r que passa pelos pontos (a, 0) e (1, -2) é
1
. ENCONTRE:
2
a) o VALOR DE a.
b) a EQUAÇÃO REDUZIDA da reta r.
20) A equação geral da reta que passa pelos pontos (-4, -2) e (1, 13) é
(A) -3x –y – 10 = 0
(B) -3x –y +10 = 0
(C) -3x +y –10 =0
(D) -3x +y + 10 = 0
(E) 3x +y + 10 = 0
21) O módulo e o argumento do número complexo Z = 1 + i é:
(A)
(D)
 2e 
  3e  

3

3
1

e 
2
4
(B)

(E)
  3e  
22) O resultado de ( 1 + i)350 é:
(A) i
(B) – i
(C) –2175
(C)


2

e 
4
2
4
(D) 2175
(E) – 2175 i
23) Dados os pontos (3, -1), (2, 3) e (a, 5), indique o valor de a de forma que os três pontos estejam alinhados.
(A) –3/2
(B) –2/3
(C) 2/3
(D) 3/2
(E) 3/4
24) O gráfico abaixo representa uma reta cuja equação é:
a)
b)
c)
d)
e)
6x + 4y – 52 = 0
–2x + 3y –12 = 0
x+y–4=0
x+y–6=0
2x + 3y –12 = 0
y
4
6
x
25) A ordenada do ponto P de abscissa 4, alinhado com os pontos A(3 ; 5) e B(-3 ; 8) é um número:
a) natural
b) inteiro positivo
c) irracional
d) racional
e) inteiro negativo
26) Os pontos A ( –1, 2 ), B ( 3 , 1 ) e C ( a , b ) são colineares. Para que C esteja sobre o eixo de abscissas, a e b
devem ser, respectivamente, iguais a:
a) 0 e 4
b) 0 e 7
c) 4 e 0
d) 7 e 0
e) 0 e 0
EXTRAS DE GEOMETRIA ANALÍTICA E DE NÚMEROS COMPLEXOS
1) Seja o número complexo z = 4i/(1+i). Determine a forma trigonométrica de z.
2) Seja z um número complexo de módulo 2 e argumento principal 120°. Escreva o conjugado de z na forma
algébrica.
3) Na figura adiante, os pontos A, B e C são as imagens dos números complexos z1, z2 e z3, no plano de ArgandGauss.
Se |z1| = |z2| = |z3| =
e  = 60°, então calcule z1 + z2 + z3.
4) Sendo z = {2.[cos(/4) + i.sen(/4)]}, calcule o conjugado de z2.
5) Calcule o produto dos números complexos cos(/6)+i.sen(/6) e cos(/3)+i.sen(/3).
6) Se z1 =
3 + i e z2 = 3 + i 3 , Determine o módulo e o argumento do produto z1.z2.
7) Sendo z = {2.[cos(/4) + i.sen(/4)]}, calcule o conjugado de z2.
8) Escreva o número complexo z = –
3 – i na forma polar.
9) O argumento do número complexo z é /6, e o seu módulo é 2. Escreva a forma algébrica de z.
10) A figura indica a representação dos números Z1 e Z2 no plano complexo. Se Z1 . Z2 = a + bi, então determine a +
b.
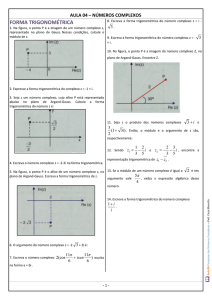
11) Na figura, o ponto P é a imagem de um número complexo z, representado no plano de Gauss. Nessas
condições, calcule o módulo de z.
12) Expresse a forma trigonométrica do complexo z = -1 + i.
13) Seja z um número complexo, cujo afixo P está representado abaixo no plano de Argand-Gauss. Calcule a forma
trigonométrica do número z é:
14) Escreva o número complexo z = -2 - 2i na forma trigonométrica.
15) Na figura, o ponto P é o afixo de um número complexo z, no plano de Argand-Gauss. Escreva a forma
trigonométrica de z.
16) O argumento do número complexo z = -2
3 + 2i é:
17) Escreva o número complexo 2(cos
11
11
 isen
) escrito na forma a + bi .
6
6
18) Escreva a forma trigonométrica do número complexo z = i 19) Escreva a forma polar do número complexo z = -
3.
3 +i.
20) Na figura, o ponto P é a imagem do número complexo Z, no plano de Argand-Gauss. Encontre Z.
21) Seja z o produto dos números complexos
3 i e
3
(1  3i ) . Então, o módulo e o argumento de z são,
2
respectivamente:
1 2
2 3
 i e z2    i , encontre a representação trigonométrica de z1  z2 .
3 5
3 5
5
23) Se o módulo de um número complexo é igual a 2 e seu argumento vale
, exiba a expressão algébrica
4
22) Sendo z1 
desse número.
24) Escreva a forma trigonométrica do número complexo
1 i
.
i
GABARITO
01) E
02) A
03) B
04) C
05) A
06) B
07) B
08) C
09) B
10) A
11) B
12)
13) C
14) A
15) D
16) A) z = 2 e  


B) z = 2  cos

3

3
 isen


3
C)
3
17)
5


 cos  isen 
2
2
2
18) C
19) a) a = 5 b) y =
20) D
21) C
22) E
23) D
1
5
x
2
2
24) E
25) D
26) D