Complexos: Forma Trigonométrica

COLÉGIO PEDRO II - CAMPUS SÃO CRISTÓVÃO III
3ª SÉRIE – MATEMÁTICA I – PROF. WALTER TADEU
www.professorwaltertadeu.mat.br
Exercícios de Números Complexos – Forma Trigonométrica - 2013
1. Determine o módulo e a tangente do argumento dos seguintes números complexos:
a) z = 4 + 3i
b) z = 2 – 2i
2. Supondo z  1  i , calcule
c) z = 3 + i
d) z = 3
e) z = 2i
f) z = a + bi
z16 na forma trigonométrica e na forma algébrica.
3. Represente os seguintes números complexos na forma não dada (algébrica ou trigonométrica).
a) 10cis

4
4. Sejam z 
c) 3cis
b) i
35
2
d) cis
5
6
e)
3 2 3 6

i
2
2






 isen  . Represente a forma trigonométrica de ( z.w ).
2  cos  isen  e w  3 cos
12
12 
4
4


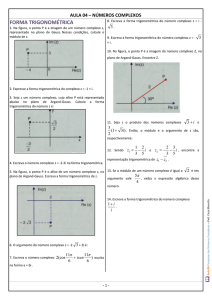
5. O número complexo z  (a, b ) representado no plano complexo mostrado na figura e
cujo módulo é
3 pode ser escrito na forma algébrica:
a) 3  i 3
b) 3  i 3
2
6. Dados z  1  2i e
a)
c)  3  i 3
2
3  3i
2
d)
e)
 3  3i
2
w  3  i , calcule:
z
w
b) w
2
c)
zw
d)
7. Qual é, em radianos, a soma dos argumentos dos números complexos z 
8. Se um número complexo z tem módulo igual a
2 e argumento igual a
w
1
3

i e w  1  i .
2 2

7
, então z tem parte real e parte
4
imaginárias, respectivamente.
a) 8 e – 8
9. Sendo z 
b) – 8 e 8
c)
8 2 e–8
d) – 8 e
8 2
e) 8 e 8
 1 i
, encontre a representação trigonométrica z .
i
10. Sendo z = cis60º, calcule na forma algébrica a soma (1 + z + z2 + z3).
3
1
; b) z  2 2; tg  1; c) z  10; tg   ; d) z  3; tg  0 ;
4
3
b
2
2
16
e) z  2; tg  Não há ; f) z  a  b ; tg   ; 2) FT: z  256cos 4  isen4 ; FA: 256;
a
3 1
2




 i ; e) 3 2.cis ; 4) 3 2  1  3 i  ; 5) e; 6) a)
3) a) 5 2 1  i ; b) cis ; c) - 3; d) 
; b) 10;
2 2 
3
2
2
2
2


Respostas: 1) a) z  5; tg  
c)
5  10 ; d) 10 ; 7)
29
; 8) a; 9)
12
2.cis
3
; 10)
4
3 .i .