Aula 04

AULA 04 – NÚMEROS COMPLEXOS
FORMA TRIGONOMÉTRICA
8. Escreva a forma trigonométrica do número complexo z = i -
3.
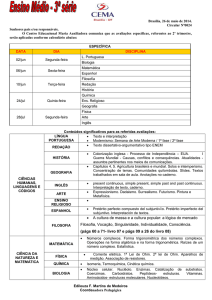
1. Na figura, o ponto P é a imagem de um número complexo z,
representado no plano de Gauss. Nessas condições, calcule o
módulo de z.
9. Escreva a forma trigonométrica do número complexo z = +i.
3
10. Na figura, o ponto P é a imagem do número complexo Z, no
plano de Argand-Gauss. Encontre Z.
2. Expresse a forma trigonométrica do complexo z = -1 + i.
3. Seja z um número complexo, cujo afixo P está representado
abaixo no plano de Argand-Gauss. Calcule a forma
trigonométrica do número z é:
11. Seja z o produto dos números complexos
3+i e
3
(1 + 3i ) . Então, o módulo e o argumento de z são,
2
respectivamente:
2 3
1 2
− i e z2 = − − i , encontre a
3 5
3 5
representação trigonométrica de z1 − z2 .
12. Sendo
4. Escreva o número complexo z = -2-2i na forma trigonométrica.
z1 =
5. Na figura, o ponto P é o afixo de um número complexo z, no 13. Se o módulo de um número complexo é igual a 2 e seu
5π
plano de Argand-Gauss. Escreva a forma trigonométrica de z.
, exiba a expressão algébrica desse
argumento vale
4
14. Escreva a forma trigonométrica do número complexo
1+ i
.
i
6. O argumento do número complexo z = -2
7. Escreva o número complexo
na forma a + bi .
2(cos
3 + 2i é:
11π
11π
+ isen
) escrito
6
6
-1-
 Aula 04:Conjuntos dos Números Complexos – Prof. Cirço Mancilla
número.