Cap 2

8
Instituto de Biofísica Carlos Chagas Filho
BFB 738 - ELETRICIDADE E ELETRÔNICA APLICADAS À BIOLOGIA
Prof.: Geraldo Cidade
Capítulo 2
Circuitos DC com Elementos Dissipativos
2. Introdução
Neste capítulo, através da revisão dos conceitos básicos vistos no capítulo 1, chegaremos a
métodos que facilitam a análise de circuitos reais. O elemento dissipativo, por excelência, é o
resistor, que transforma em calor grande parte da energia para ele transferida. Os componentes
existentes no mercado trazem especificado em seu corpo o valor da taxa de energia (potência
elétrica) máxima que podem dissipar sem que sofram quaisquer danos. Trazem impressas também
informações sobre seu valor nominal e a tolerância (porcentagem máxima de variação ohmica) que
lhes foram impostas durante sua fabricação; salvo alguns casos especiais, esta tolerância é de,
normalmente, ± 1%, ± 5% ou ± 10%.
2.1. Circuito Elétrico Elementar
Qualquer circuito elétrico real, por mais simples que seja, deverá conter em sua configuração
pelo menos uma resistência elétrica física (resistor), ou mesmo sua manifestação através de outros
elementos, dado seu caráter dissipativo.
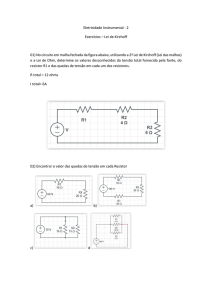
Ao conectar um gerador de tensão DC com E volts nos terminais de um resistor de R ohms
(Fig. 2.1a) , por este fluirá uma corrente elétrica de I ampères. A relação entre estes dois valores é
estabelecida pela lei de Ohm, da forma mais apropriada:
I
V
R
R
ou
V
I
V  R. I
ou
(2.1)
Ao ligar um gerador ideal de corrente DC, com I ampères, em um resistor de R ohms, sobre
seus terminais será estabelecida uma ddp de V volts (Fig. 2.1b).
(a)
(b)
a
a
+
+
E
R
I
R
I
V
_
_
b
b
Figura 2.1. Circuito elétrico elementar empregando fontes de tensão (a) e de corrente (b).
2.2. Resistências em Série
9
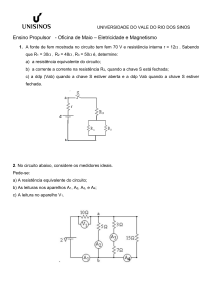
Na fig. 2.2a observa-se uma única corrente elétrica I, que flui através dos resistores R1 e R2.
(a)
(b)
a
+
a
I
R1
+
V
_
+
c
_
R2
+
Vac
I1
I
G1
I2
G2 V
_
Vcb
b
_
b
Figura 2.2. Circuitos em série (a) e em paralelo (b).
Segundo a lei de Ohm:
Vac = R1.I sobre R1
(2.2)
Vcb = R2.I sobre R2
(2.3)
Logo, a tensão entre os terminais a e b será:
Vab = Vac + Vcb
(2.4)
e igual à V, pois estes também são os terminais da fonte geradora. Isto verifica a primeira lei de
Kirchoff, que enuncia: “A soma das tensões em torno de uma malha fechada é nula”. A expressão
(2.4) pode ser reescrita da seguinte maneira:
Vac + Vcb - V = 0
(2.5)
ou seja, todas as tensões medidas foram referenciadas segundo o sentido da corrente (convencional).
Substituindo-se a expressões (2.2) e (2.3) em (2.4), obtém-se:
Vab = R1.I + R2.I = (R1 + R2). I
(2.6)
Definindo como REQ a resistência equivalente da combinação série vista pelos terminais da fonte,
tem-se:
Vab = REQ . I
(2.7)
que, quando comparada à expressão (2.6), nos fornece:
REQ = R1 + R2
(2.8)
Tomando-se as expressões (2.2) e (2.3) em função de I, obtém-se:
I
Vac Vcb

R1
R2
, ou seja,
Vac R1

Vcb R2
(2.9)
10
que define a lei de divisão de tensão: “As tensões sobre resistores percorridos por uma mesma
corrente são diretamente proporcionais aos valores das resistências envolvidas”. Com base nesta
lei, existe um processo muito simples para determinar a tensão sobre um resistor de uma
combinação série, em que:
Vcb
R
R2
 2 
V
REQ R1  R2
Vcb 
ou
R2
V
R1  R2
(2.10)
2.3. Resistências em Paralelo
Na fig. 2.2b pode-se observar uma única tensão V, comum às resistências e aos terminais da
fonte. Definamos como condutância a qualidade de um componente em permitir a passagem de
corrente. Então:
G
1
R
R
ou
1
G
(2.11)
Pela lei de Ohm:
I1 = G1 .V
(2.12)
e I2 = G2 .V
(2.13)
logo, a corrente que entra pelo ponto (nó) a é:
I = I1 + I2 = (G1 + G2).V = GEQ.V
 GEP = G1 + G2
(2.14)
(2.15)
e utilizando a relação (2.11), obtém-se:
1
1
1


REQ R1 R2
ou
REQ 
R1 . R2
R1  R2
(2.16)
Verifica-se daí a segunda lei de Kirchoff, ou, simplesmente, lei dos nós: “A soma das
correntes em um nó é nula”. Por convenção, as correntes que entram são positivas e as que saem
negativas. Partindo da expressão (2.14), tem-se:
I - (I1 + I2) = 0
I1 + I2 - I = 0
para o nó a, e
para o nó b.
A expressão (2.15) mostra que “a condutância equivalente à combinação paralela de
diversas condutâncias equivale à soma dos valores daquelas”, ou que “o inverso da resistência
equivalente à combinação paralela de diversas resistências corresponde à soma dos inversos dos
valores daquelas” (2.16).
11
Ao comparar as expressões (2.12), (2.13) e a última parte de (2.14), em função de V:

I1
I2
I


G1 G2 G EQ
(2.17)
I1 G1 R2


I 2 G2 R1
(2.18)
ou seja, a lei de divisão de corrente enuncia que: “as correntes que percorrem condutores
submetidos à uma mesma tensão são diretamente proporcionais aos valores das respectivas
condutâncias”, ou que “as correntes que percorrem resistores submetidos a uma mesma tensão são
inversamente proporcionais aos valores das respectivas resistências”. De (2.17), a expressão de I1
(ou I2) poderá ser determinada:
G1
I1
I
I


 I1  I . G  G
G1 G1  G2 G EQ
1
2
(2.19)
cujo formato é análogo ao da divisão de tensão em circuitos série (vide (2.10)) . Cabe ressaltar, que
em circuitos paralelos é muito mais conveniente trabalhar com condutâncias ao invés de
resistências.
2.4. Geradores Reais
Na realidade física não existe fontes ideais. Suponha que num gerador de tensão com valor
V, finito, seus terminais sejam colocados em curto-circuito. Para que o gerador mantivesse o mesmo
valor de tensão de saída sobre o curto-circuito (resistência nula), ele deveria ser capaz de debitar
corrente infinita, o que não é possível.
Da mesma forma, para que um gerador de corrente fosse capaz de fornecer um valor I,
finito, com seus terminais em aberto (circuito aberto), ou seja, sobre uma resistência infinita, teria
que estabelecer entre eles uma tensão infinita, o que também não é possível.
2.4.1. Gerador Real de Tensão
Nos geradores reais de tensão, na medida em que mais corrente é solicitada, a ddp entre os
terminais tende a diminuir. Isto se deve às limitações do gerador, que retém parte da tensão de saída
em uma resistência interna a ele, por onde passa a mesma corrente. Assim, representa-se um gerador
real de tensão por um gerador ideal em série com uma resistência interna (Ri) ou de saída (fig.
2.3a). Um gerador ideal seria aquele com resistência nula.
12
2.4.2. Gerador Real de Corrente
Num gerador real de corrente, na medida em que a resistência ligada em seus terminais
aumenta, mais a corrente fornecida diminui. Tudo se passa como se houvesse uma divisão de
corrente entre a resistência de carga (RL) e outra paralela (Ri), interna ao gerador, conforme
mostrado pela fig. 2.3b; o gerador real é representado por um gerador ideal (resistência interna
infinita) em paralelo com Ri.
(a)
Ri
(b)
a
a
+
V
RL
_
Ri
I
RL
b
b
Figura 2.3. Geradores reais de (a) tensão e de (b) corrente.
2.4.3. Transformação de Fontes
Considerando uma fonte real de energia, sabe-se que, com os terminais abertos, a tensão de
saída é máxima, já que:
a) no gerador real de tensão, não havendo corrente, não haverá queda na carga RL;
b) no gerador real de corrente, a tensão de saída equivale à Ri.I, uma vez que toda a corrente
circulará através de Ri.
Do contrário, colocando os terminais em curto-circuito, a corrente de saída será máxima, já que:
a) no gerador real de tensão, o valor da corrente será limitada pelo valor de Ri, ou seja,
V
;
Ri
b) no gerador real de corrente, toda a corrente circulará pelo curto-circuito, e será I.
A fig. 2.4 mostra que um mesmo gerador poderá ser representado como de tensão ou de
corrente, estabelecendo, portanto, uma dualidade entre estes dois tipos de representação.
Ri
a
a
+
V
I
_
Ri
b
V = Ri . I
b
I = V / Ri
Figura 2.4. Transformação entre fontes reais.
13
Para que os valores de tensão em aberto, e de corrente em curto-circuito, sejam os mesmos
nas duas representações de uma mesma fonte de energia, torna-se necessário que ambas exibam
uma mesma resistência interna, que relacione a tensão e a corrente das fontes ideais. Supondo o
exemplo abaixo, se a resistência de carga RL for de 40 Ω, calculando no circuito do gerador de
tensão:
VL 
RL
40
.V 
.100  80V
RL  Ri
40  10
e
IL 
VL 80

 2A
RL 40
Calculando pelo gerador de corrente:
1
GL
10
IL 
. I  40 .10 
 2A
1
1
Gi  G L
5

10 40
10
+
100V
a
IL
V L  R L . I L  2  40  80V
a
100V
10
RL
_
e
b
10A
10
RL
IL
b
Com respeito aos terminais a e b, as duas representações conduziram ao mesmo resultado,
que é válido para qualquer valor de RL. A escolha de uma representação ou outra é ditada pelas
conveniências de cálculo do circuito. Na prática, quando a resistência de saída de um gerador for
muito baixa, quando comparada à carga, de tal forma que as variações desta pouco influenciam a
tensão entre os terminais de saída, costuma-se utilizar a representação do gerador de tensão. De
forma análoga, se a resistência de saída for alta, quando comparada com a carga, convém utilizar a
representação do gerador de corrente.
2.4.4. Teoremas de Thèvenin e Norton
A generalização dos conceitos vistos anteriormente leva a dois teoremas de grande aplicação
no cálculo de circuitos elétricos, que são: o teorema de Norton (fonte de corrente) e o de Thèvenin
(fonte de tensão).
2.4.4.1. Teorema de Thèvenin
“Qualquer par de terminais de um circuito ativo poderá ser representado por um gerador
ideal de tensão E, com uma resistência de saída em série R”. O valor de E corresponde à tensão
14
medida com os terminais em aberto, e o de R a partir da divisão de E pela corrente produzida com
os mesmos terminais em curto-circuito (fig. 2.5a).
2.4.4.2. Teorema de Norton
“Qualquer par de terminais de um circuito ativo poderá ser representado por um gerador
ideal de corrente I, com uma condutância de saída, paralela, Gi”. O valor de I é calculado a partir
da corrente que flui entre os terminais a e b, na condição de curto-circuito, e o de Gi dividindo-se I
pelo valor da tensão entre a e b, com os terminais em aberto (fig 2.5b). De um teorema pode-se
chegar ao outro através do método da transformação de fontes.
(a)
(b)
Ri
a
a
+
E
I
G i=
I
_
1
Ri
b
b
Figura 2.5. Teoremas de (a) Thèvenin e de (b) Norton.
Vamos ilustar a aplicação dos teoremas com um exemplo simples. A partir do circuito
ilustrado a seguir, vamos determinar os equivalentes de Thèvenin e Norton.
50
c
50
a
+
50
100V
_
b
1) Cálculo da tensão em aberto: Vab 
50
.100  50V . Para calcular a corrente de curto50  50
circuito (ISC), os pontos a e b deverão ser conectados.
50
c
50
a
+
50
100V
ISC
_
b
2) Cálculo da corrente de curto-circuito (ISC):
15
a) determinar o valor de REQ entre c e b: REQ 
50
 25 ;
2
b) calcular o valor da tensão entre c e b: Vcb 
25
100
.100 
V;
50  25
3
c) calcular a corrente de curto circuito:
3) Cálculo da resistência de saída: R 
75
I SC 
Vcb
100
2

 A.
50 3  50 3
Vab
50

 75
I SC 2 / 3
a
a
+
2
A
3
50V
_
75
b
b
2.5. Anulação e Superposição de Fontes
2.5.1. Anulação de Fontes
Para anular uma fonte de tensão basta substituí-la por um curto-circuito. Para uma fonte real
de tensão ser anulada, deverá ser substituída pela sua resistência interna. Por outro lado, uma fonte
ideal de corrente possui uma resistência de saída infinita, e para anulá-la basta substituí-la por um
circuito aberto. Para que uma fonte real de corrente seja anulada, deverá ser substituída por sua
resistência interna.
Representações de tensão e corrente de uma fonte
Ri
a
a
+
E
Ri
I
_
b
b
Anulação de Fontes
Ri
a
a
Ri
b
b
16
Se desejarmos apenas saber qual o valor da resistência de saída entre os terminais a e b do
exemplo dado no subítem 2.4.4.2, empregando o método de anulação de fontes, esta poderá ser
facilmente obtida a partir da seqüência abaixo.
50
50
a
50
50
a
a
25
75
b
b
b
2.5.2. Superposição de Fontes
A propriedade de linearidade dos componentes ativos pemite simplificar o cálculo de
circuitos elétricos com mais de um gerador através da anulação seletiva de fontes. O método
consiste em anular todas as fontes menos uma, repetindo-o para todas as demais. Por exemplo, dado
o circuito:
10
a
+
+
10V
_
10
1A
10
Vab= ?
_
b
1) anular, seletivamente, a fonte de tensão e calcular a tensão entre os terminais a e b, parte da
contribuição da fonte de corrente:
10
a
1A
10
a
10
10
1A
b
10
10
b
Vab'  1  3,33  3,33V
2) anular a fonte de corrente e calcular a contribuição da fonte de tensão entre os terminais a e b :
10
a
10
+
10V
10
10
_
a
+
5
10V
_
b
b
17
Vab" 
5
.10  3,33V
5  10
Vab  Vab'  Vab''  0
3) Valor da tensão total equivale à contribuição de Vab' e Vab'' :
2.6. Métodos para o Cálculo de Circuitos
Para calcular circuitos, todos os métodos baseiam-se nos mesmos princípios, ou seja, na lei
de Ohm e nas duas leis de Kirchoff (lei dos nós de das malhas). Os conceitos apresentados neste
capítulo abrange os princípios básicos, simplificando os cálculos e reduzindo a possibilidade de
erros.
2.6.1. Leis de Kirchoff
Através da aplicação das duas leis de Kirchoff à todas as malhas e nós do circuito em
questão, estabelece-se um sistema de equações que será resolvido em função da variável desejada.
Maxwell metodizou a aplicação das leis com correntes e tensões auxiliares, o que facilta o cálculo
de circuitos através do emprego de matrizes e determinates.
2.6.2. Método da Composição de Elementos
Procura-se fazer, sucessivamente, a composição de resistências em série e em paralelo,
obtendo-se circuitos mais simplificados. Os geradores também podem ser compostos, isto é,
somando-se algebricamente as fontes de corrente em paralelo e as de tensão em série.
50
_ 10
+
+
a
60
a
+
10V
10
50V
40V
_
10
_
b
b
a
5A
20
2A
20
a
50
3A
b
2.6.3. Método de Divisão de Tensão e de Corrente
10
50
b
18
Este método aplica os conceitos da divisão de tensão e de corrente para os cálculos rápidos
de circuitos.
2.6.4. Transformação de Fontes
Muitas vezes, um circuito pode parecer complexo e de cálculo trabalhoso. Até mesmo a
forma de desenhá-lo pode facilitar ou dificultar sua interpretação. Através do emprego da
transformação de fontes (tensão  corrente) sua simplicação torna-se evidente.
a
30
1A
60
30
60
1A
+
20
Vab= ?
+
30V
+
60V
_
_
b
_
a
30
+
60
30V
_
60
1A
20
60
60
+
30
60V
1A
_
+
30V
+
+
_
_
60V
_
60
20
60V
b
b
a
1A
60
1A
60
1A
60
20
3A
b
20
20
b
2.6.5. Superposição de Fontes
É muito útil quando mais de um gerador encontra-se no circuito. Um bom exemplo seria
calcular o exemplo dado no subítem anterior através deste método.
19
2.6.6. Teoremas de Norton e Thèvenin
Levam diretamente à simplificação mais drástica do circuito, exatamente sobre os terminais
onde se deseja determinar os valores das variáveis. Impõem, a priori, o cálculo da corrente de curtocircuito e da tensão de circuito aberto, que poderão ser determinadas utlizando qualquer um dos
outros métodos.
2.7. Potência Elétrica
Se um resistor, onde se estabeleceu uma ddp, é percorrido por uma corrente I, relacionadas
entre si pela lei de Ohm, a quantidade de carga elétrica que flui num tempo t, é:
Q
=
x
I
t
(2.20)
(Coulombs) (Ampères) (segundos)
A taxa de energia dissipada na resistência denomina-se potência elétrica, dada pelas relações:
P = V x I
(Watt)
P = R x I2
ou
ou
2
(Volt)(Ampère)
(Watt) (Ohm)(Ampère )
P = V2 / R
(Watt)
(Volt2) / (Ohm)
A energia dissipada em um tempo t é dada por:
W = P x t
(Joule) (Watt)(segundo)
2.7.1. Potência Fornecida e Dissipada
Nas convenções impostas ao circuito elétrico abaixo, consideramos o produto tensão x
corrente sobre a resistência como positivo, ou seja, a corrente fluindo do polo positivo para o
negativo.
+
+
V
I
_
I
V
_
A lei da conservação de energia nos leva a concluir que a potência dissipada na resistência é igual à
fornecida pela fonte. O produto tensão x corrente sobre a fonte exibe o mesmo valor numérico, mas
é negativo, uma vez que a corrente flui para o polo negativo. Daí, esta mudança de sinal significa a
geração, ou fornecimento, de energia. Conforme os sentidos convencionais, tal produto poderia ser
positivo ou negativo, e a resistência positiva ou negativa. O conceito de resistência negativa, como
representativa de geradores, é muito útil na análise de circuitos.
20
2.7.2. Máxima Transferência de Potência
Deseja-se determinar qual o valor do resistor de carga que absorve o máximo de potência
fornecida por um gerador real. Na figura mostrada abaixo, define-se a potência dissipada pela carga
R.
r
a
+
E
I
R
I
_
b
P  R. I 2
ou
P  E2
R
(r  R)2
Considerando-se uma carga ajustável, derivamos a expressão da potência, e determinamos o valor
de R, igualando a derivada à zero, o que corresponde ao máximo valor de potência transferida.
Assim:
2


dP
2 (R  r )  2R (r  R )
2 rR
E 
E
4
dR
(r  R)
(r  R)3


Igualando o numerador à zero:
E 2 ( r  R)  0
temos que:
Rr
Então, para que a transferência de potência seja máxima, o resistência de carga R deverá ser igual
àquela interna ao gerador. Neste caso, diz-se que a carga encontra-se casada (“matched”) com o
gerador.