aula05 - Evandro Bastos

Circuitos em Série-Paralelo
Evandro Bastos dos Santos
26 de Março de 2017
1
Circuitos em Série-Paralelo
Nas aulas anteriores vimos como calcular a resistência equivalente, tensão e corrente em
arranjos em série e paralelo, separadamente. Hoje veremos problemas em que temos uma
combinação desses arranjos. Além disso, veremos casos de curto-circuito e circuitos abertos.
Exemplo 1
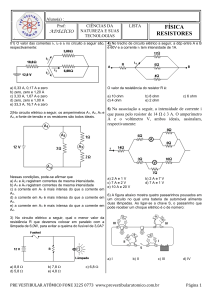
Determine a corrente I4 e a tensão V2 no circuito abaixo.
Figura 1: Exemplo 1.
Vamos separar em dois blocos. O bloco A que contém os resistores 1,2 e 3, e o bloco B
que contem o resistor R4 . A tensão nos dois blocos é a mesma pois estão em paralelo.
Figura 2: Exemplo 1.
Aplicando a lei de Ohm temos que
I4 =
E
E
12
=
=
= 1, 5A
RB
R4
8
(1)
No ramo que está os resistores 1,2 e 3, podemos dividir em dois blocos. Bloco C para o
resistor 1 e o bloco D para os resistores 2 e 3. Combinando os resistores R2 e R3 ,
1
RD = R2 ||R3 =
3·6
18
=
= 2Ω
3+6
9
(2)
Aplicando a regra do divisor de tensão
V2 =
RD E
2 · 12
=
= 4V
RD + RC
2+4
(3)
Exemplo 2
Determine as tensões e as correntes indicadas no circuito abaixo.
Figura 3: Exemplo 2.
Novamente vamos separar em blocos, A com R1 , R2 e R3 e B com R4 e R5 .
Figura 4: Exemplo 2.
Então usando a lei de Ohm temos que
−1 −1
1
1
1
1 1 1
RA =
+
+
=
+ +
= 1, 2Ω
R1 R2 R3
6 6 2
−1 −1
1
1
1
1
RB =
+
=
+
= 4, 8Ω
R4 R5
8 12
2
(4)
(5)
Como A e B estão em série
Req = RA + RB = 1, 2 + 4, 8 = 6Ω
(6)
V1 = Is RA = 4 · 1, 2 = 4, 8V
V5 = Is RB = 4 · 4, 8 = 19, 2V
(7)
(8)
Assim
Aplicando a lei de Ohm,
V5
19, 2
=
= 2, 4A
R4
8
4, 8
V2
=
= 0, 8A
I2 =
R2
6
I4 =
(9)
(10)
Exemplo 3
Determine as tensões V1 , V3 e Vab no circuito abaixo.
Figura 5: Exemplo 3.
Como temos duas fontes, 18V e 6V, vamos considerar que a fonte resultante é
ET = E1 + E2 = 18V − 6V = 12V
(11)
com Is no sentido de E2 .
Então podemos determinar V1 e V3 , pela regra do divisor de tensão.
R1 E
5 · 12
=
= 7, 5V
R1 + R2
5+3
R3 E
6 · 12
V3 =
=
= 9V
R3 + R4
6+2
V1 =
(12)
(13)
A tensão no circuito aberto Vab é determinada aplicando a lei de Kirchoff para as tensões
V1 − V3 + Vab = 0
7, 5 − 9 + Vab = 0
Vab = 1, 5V
3
(14)
(15)
(16)
As correntes I1 e I3 são determinadas pela lei de Ohm,
V1
7, 5
=
= 1, 5A
R1
5
V3
9
I3 =
= = 1, 5A
R3
6
I1 =
(17)
(18)
Pela lei de Kirchoff das correntes temos que
Is = I1 + I3
Is = 1, 5 + 1, 5 = 3A
(19)
(20)
Nesse exemplo percebemos mostramos que podemos, não apenas calcular a tensão entre
os terminais de um elemento, mas podemos calcular a tensão entre dois pontos quaisquer
de um circuito.
Exemplo 4
Determine no circuito abaixo as tensões V1 , V2 e a corrente I.
Figura 6: Exemplo 4.
É bem difícil analisar o circuito como mostrado na figura 6, mas ao redesenhar o circuito
conforme mostra na figura 7
Figura 7: Exemplo 4 redesenhado
Portanto, já podemos determinar que
V2 = E1 = −6V
Aplicando a lei de Kirchoff para as tensões temos que
4
(21)
−E1 + V1 − E2 = 0
V1 = E2 + E1 = 18 + 6 = 24V
(22)
(23)
Aplicando a lei de Kirchoff para as correntes na junção a, temos que
I = I1 + I2 + I3
V1
E1
E1
+
+
I=
R1 R4 R1 + R3
14 6
6
I=
+ +
6
6 12
I = 5, 5A
(24)
(25)
(26)
(27)
Exemplo 5: Circuito em cascata
Um circuito em cascada é aquele em que á uma repetição da sua forma. Veja o exemplo
abaixo, e determina a tensão e a corrente em todos os resistores.
Figura 8: Exemplo 5
Para solucionar esse tipo de circuito temos que determinar a resistência equivalente para
obter a corrente total Is .
Assim temos que
RA = R5 + R6 = 1 + 2 = 3Ω
−1 −1
1
1
1 1
+
=
+
= 2Ω
RB =
R4 RA
6 3
RC = R3 + RB = 4 + 2 = 6Ω
−1 −1
1
1
1 1
RD =
+
=
+
= 3Ω
R2 rC
6 6
RE = R1 + RD = 5 + 3 = 8Ω
(28)
(29)
(30)
(31)
(32)
Assim a corrente será
Is =
240
= 30A
8
(33)
Como R2 e RC são iguais. A corrente I2 será, aplicando a regra do divisor de corrente
5
I3 =
Is R2
Is
=
= 15A
RC
2
(34)
E para a corrente I6 , aplicando a regra do divisor de corrente, temos
6
I3 R6
= 15 = 10A
RA
9
(35)
V6 = R6 I6 = 2 · 10 = 20V
(36)
I6 =
Logo, temos que, pela lei de Ohm
Desafio(Valendo 0,2 na AV1): Determine o valor da resistência equivalente do circuito
em cascata abaixo, sendo R1 = 2Ω e R2 = 4Ω.
Figura 9: Desafio
Exercícios do livro: 2, 4, 10, 15, 26 e 27
6