Problema 2

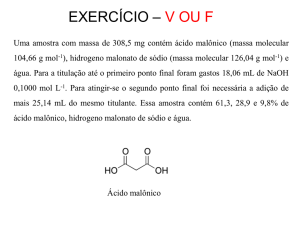
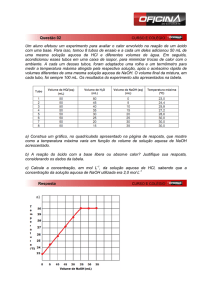
RESOLUÇÃO DE PROBLEMAS DE CONCENTRAÇÃO DE SOLUÇÕES - CAPÍTULO 2
DA APOSTILA
Problema 1
Qual o volume final em litros da mistura dos seguintes volumes de água: 5,4 103 L, 2,36 mL e
1,2 10-3 L?
5,4 103 L =
2,36 mL
=
1,2 10-3 L? =
volume total
0,0054 L
0,00236 L
0,0012 L
0,08 L
Problema 2
Qual a porcentagem de cobre no sulfato de cobre pentahidratado puro? E se o sal tivesse 95%
de pureza?
a) Porcentagem de Cu no sal puro
CuSO4.5H2O massa molar = 63,5 + 32 + 4.16 + 5(16+2)= 249,5
249,5 g do sal contem .......63,5 g Cu
100 g conterão................ x
100.63,5
= 24,17
%Cu = 25,45
y
249,5
b-) Porcentagem de Cu no sal impuro
249,5 g do sal puro contem......................63,5 g Cu
100 g do sal impuro contem ..........95 g do sal puro contem ......................... y
95.63,5
= 24,17g Cu
y
249,5
100 g do sal impuro contem 24,17g Cu
%Cu = 24,17%
Problema 3
Uma mistura de sais contém 20%N; 10%P e 8%K. Quantos quilogramas de N, P e K estão
presentes em 500 kg dessa mistura?
100 kg da mistura contem ........... 20 kg de N.............10 kg de P.......................8 kg K
500 kg da mistura conterão ....... x ..................... y ................................ z
x = 100 kg N
y = 50 kg P
z = 40 kg K
Problema 4
Quantos mols de nitrato de cálcio existem em 1,2 105 g desse sal?
massa molar Ca(NO3)2 = 40 + 2( 14 + 3.16 ) = 164
164 g de Ca(NO3)2 equivale a ............ 1 mol
1,2 105 g equivalerão a ......................x
x
1,2.105
 731,7 mols
164
a massa corresponde a 731,7 mols
Problema 5
Qual a massa de potássio existente na mistura de 10g nitrato de potássio com 2000 mg de
sulfato de potássio? Expressar o resultado em miligramas e em mols
KNO3 massa molar = 101
K2SO4 massa molar = 174
101 g KNO3 contem 39 g K
10 g conterão ............x
x = 3,861g K
174g K2SO4 contem 78 g K
2 g conterão...............y
y = 0,896 g K
massa total K em mg = 4,758g ou 4758 mg
massa total em mols:
39g K correspondem a ........... 1 mol
4,758g corresponderão a ....... x
x = 0,122 mols K
Problema 6
São misturados 0,5 kg de carbonato de cálcio a um produto com densidade 1,3 g cm-3 e
contendo originalmente 156 mg Ca kg-1. Esse produto forma uma camada de 10 cm num
tanque com 1,5 m2 de área. Qual será o novo teor de cálcio do material?
Volume do produto = 1,5 m2 x 0,10 m = 0,15 m3 = 150.000 cm3
Massa do produto = V . d = 150.000 x 1,3 = 195.000g = 195 kg
CaCO3 massa molar = 100
100 kg CaCO3 contem .................. 40g Ca
0,5 kg conterão .............................. x
x = 0,2 kg ou 200g Ca
A adição do produto corresponderá a um acréscimo de 200g de Ca a 195 kg do produto
Ou seja : 200.000 mg Ca/195 kg = 1025,6 mg/kg
Como o produto já contem cálcio o novo teor será:
156 + 1025,6 = 1181,6 mg Ca kg -1
Problema 7
Quantos gramas de sulfato de potássio devem ser diluídos em 105 mL de água para se obter
uma solução de concentração 25 mg K L-1?
A solução desejada contem
1 litro........................25 mg de K
100 litros .................. x
K2SO4
massa molar = 174
78g K estão contidos em..... 174 g K2SO4
2,5g estarão contidos em..... x
x = 2500 mg ou 2,5g K
y = 5,58g K2SO4
Problema 8
Quantos gramas de sulfato de sódio devem ser dissolvidos em 500 mL de água para se obter
uma solução 0,02 mol L-1 Na+?
número de mols de Na necessários: n = 0,02 mol/L . 0,5 L = 0,01 mol Na
Na2SO4 massa molar = 142
142 g de Na2SO4 corresponde a ............. 1 mol Na2SO4
ou ....... 2 mols Na
x g corresponderão a .................................................................... 0,01 mols Na
x = 0,71 g Na2SO4
Problema 9
Quantos miligramas de potássio existem em 20 mL de uma solução de dicromato de potássio
0,02 mol L-1 ?
número de mols de sal no volume de solução dado:
n = 0,020L . 0,02 mol/L = 0,0004 mols K2Cr2O7
massa molar K2Cr2O7 = 294
1 mol K2Cr2O7 contem .................2 mols K............... ou 78g K
0,0004 mols K2Cr2O7 conterão ............................................ y
y = 0,0312 g ou 31,2 mg K
Problema 10
Diluem-se 25 mL de uma solução a 500 ml. A análise da solução diluída revela as
concentrações 112 mg L-1 K+; 25 mg L-1 N e 28 mg L-1 P. Qual a concentração desses
elementos na solução inicial em mol L-1?
Têm-se inicialmente 25 mL de uma solução que será chamada A
Por diluição, a partir dos 25 mL da solução A, serão obtidos 500 mL de uma solução B
1 litro de solução B contem...... 112 mg K ......... 25 mg N ............ 28 mg P
0,5 L de solução B contem ....... x mg K ........... y mg N ............. z mg P
x = 56 mg K
y = 12,5 mg N
z = 14 mg P
Esses 56 mg de K vieram de 25 mL da solução A
25 mL de solução a contem ............. 56 mg K ...............12,5 mg N .................. 14 mg P
1000 mL conterão ............................ x ............................ y ............................... z
x = 2240 mg K
y = 500 mg N
z = 560 mg P
Problema 11
20 mililitros de uma solução cuja concentração é 800 mg L-1 CaCl2 são transferidos para um
balão volumétrico de 250 mL, completando-se o volume. Qual a concentração de íons cálcio e
cloreto na solução diluída em mg L-1?
20 mL de solução inicial A são diluídos para se obter 250 mL de uma solução B
1000 mL de solução A contem................800 mg CaCl2
20 mL conterão........................................ x
x = 16 mg CaCl2
Esses mesmos 320 mg de CaCl2 vão estar em 250 mL da solução B
massa molar de CaCl2 = 64
111 mg CaCl2 contem .........40 mg Ca.............71 mg Cl
16 mg contem......................... x .......................... y
x = 5,76 mg Ca
y = 10,23 mg Cl
Essas massas estão em 250 mL da solução diluída B
250 mL solução B contem ................... 5,76 mg Ca .....................10,23 mg Cl
1000mL contem .................................... x ....................................... y
x = [Ca] = 23 mg L-1
y = [Cl] = 40,9 mg L-1
Problema 12
Qual será a concentração de nitrogênio em mg L-1 nas soluções: 0,12 mol L-1 KNO3; 0,08 mol
L-1 de (NH4)2SO4 e 0,048 mol L-1 de NH4NO3 ?
Solução 0,12 mol L-1 KNO3 será 0,12 mol L-1 N
1 mol N corresponde a 14 g N
0,12 x 14 = 1,68
0,12 mol L-1 N = 1,68 g L-1 N
Solução 0,08 mol L-1 (NH4)2SO4 será 0,16 mol L-1 N
1 mol N corresponde a 14 g N
0,16 x 14 = 2,24
0,16 mol L-1 N = 2,24 g L-1 N
Solução 0,048 mol L-1 NH4NO3 será 0,096 mol L-1 N
1 mol N corresponde a 14 g N
0,096 x 14 = 1,34
0,048 mol L-1 N = 1,34 g L-1 N
Problema 13
Quantos mililitros de uma solução 0,12 mol L-1 K3PO4 devem ser adicionados a um balão de
500 mL para se obter uma solução 0,03 mol L-1 K+?
Solução A  0,12 mol L-1 K3PO4
Solução B  0,03 mol L-1 K
1000 ml de solução B contem ........... 0,03 mols K
500 mL conterão .................................... x
x = 0,015 mols K
Essa quantidade de K será fornecida pela solução A
1000 mL de solução A contem ................. 0,12 mols K3PO4 ............... 0,36 mols K
x mL conterão............................................................................................ 0,015 mols K
x = 41,7 mL
Problema 14
Qual a massa de produto necessária para preparar 60 L de uma solução de concentração 1,3
% NaOH
100 g de solução 1,3 % NaOH devem conter 1,3 g NaOH
admitindo que a densidade da solução seja 1g/cm3 ou 1 g/ml
100 mL de solução 1,3 % NaOH devem conter 1,3 g NaOH
0,1 L de solução 1,3 % NaOH devem conter 1,3 g NaOH
60 L de solução 1,3 % NaOH devem conter x g NaOH
x = 780 g naOH ou 0,78 kg
Problema 15
Dispõe-se de 650 kg de um xarope A contendo 25% em peso de sacarose. Pretende-se obter
um xarope C com concentração 35% em sacarose misturando A com outro xarope B cuja
concentração é 43% em sacarose. Qual a massa do xarope B necessária?
100 kg do xarope A contem......... 25 kg de sacarose
650 kg conterão............................ x
x = 162,5 kg de sacarose
100 kg do xarope B contem....... 43 kg de sacarose
M kg do xarope B conterão ..... y
y = 0,43 M kg
Serão preparados portanto (650+M) kg do xarope C que conterá (162,5+0,43M) kg de
sacarose
100 kg do xarope C devem contem............35 kg de sacarose
(650+M) kg do xarope C contem............... (162,5+0,43M)
M= 812,5 KG
RESOLUÇÃO DE PROBLEMAS DE EQUILÍBRIO QUÍMICO - CAPÍTULO 3 DA
APOSTILA
Problema 1
Em uma solução 0,002 mol L-1 de uma base sabe-se que 10% das moléculas são ionizadas.
Calcule a constante de ionização.
B + H2O  BH + OH(Cb-x)
x
x
[OH-] = [BH+] = Cb . 0,10
Kb 
[OH  ].[ BH  ]
x2
(Cb.0,1) 2
(0,0002) 2



 2,22.10  5
B
(Cb  x ) Cb.(1  0,1)
0,002.0,9
Problema 2
Faz-se uma mistura de 138g de álcool etílico (CH3-CH2OH) e 60g de ácido acético(CH3COOH). Sabendo-se que 90,5% do ácido foi esterificado, calcular a constante de equilíbrio
dessa reação em termos de concentração.
Massa molar álcool etílico = 46
Massa molar ácido acético = 60g
138 g de álcool = 3 mols
60 g de ácido = 1 mol
CH3-CH2OH + CH3-COOH  CH3-COO.CH2-CH3 + H2O
tempo zero
3 mol/V
+
1 mols/V
0
0
x mols de ácido reagem com x mols de álcool e produzem x mols de éster e x mols de água.
Restam no equilíbrio:
concentrações
no equilíbrio
(3-x)/V
(1-x)/V
x/V
x/V
Se 90,5% do ácido foi esterificado:
x 90,5 1 mol

.
V 100
V
x = 0,905
x x
.
[ester ].[água ]
x2
(0,095) 2
V V
K



 4,1
[alcool ].[ácido ] (1  x ) (3  x ) (1  x )(3  x ) 0,095.2,095
.
V
V
Problema 3
Os óxidos de nitrogênio N2O4 e NO2 participam do equilíbrio:
N2O4  2NO2
Sabendo-se que nesse equilíbrio tem-se uma massa total de 0,764g ou 0,012 mols desses gases,
ocupando um volume total de 0,486 L, calcule a constante desse equilíbrio em termos de
concentração.
Massa de NO2 = x gramas
Massa de N2O4 = y gramas
Massa molar N2O4 = 92
Massa molar NO2 = 46
x + y = 0,764 g
x
y

 0,012 mols
46 92
x (0,764  x )

 0,012 mols
46
92
x + 2.(0,764-x) = 1,104
x = 0,424 g NO2
y = 0,340g N2O4
número de mols de NO2 = 0,424 / 46 = 0,00922
número de mols de N2O4 = 0,340 / 92 = 0,00370
 0,00922 


0,486 

K
0,00370
0,486
2
 0,047
Problema 4
240 kg de ácido acético são misturados a 138 kg de álcool etílico. Qual a quantidade em peso
de todas as substâncias presentes quando o equilíbrio for atingido, sabendo-se que Kc = 4?
Massa molar álcool etílico = 46
Massa molar ácido acético = 60g
138 g de álcool = 3 mols
240 g de ácido = 4 mols
CH3-CH2OH + CH3-COOH  CH3-COO.CH2-CH3 + H2O
tempo zero
3 mol/V
+
4 mols/V
0
0
x mols de ácido reagem com x mols de álcool e produzem x mols de éster e x mols de água.
Restam no equilíbrio:
concentrações
no equilíbrio
(3-x)/V
(4-x)/V
x/V
x/V
x x
.
[ester ].[água ]
x2
V
V
K4


[alcool ].[ácido ] (3  x ) (4  x ) (3  x )( 4  x )
.
V
V
3x2 + 28x + 48 = 0
massa de ácido acético
massa de álcool etílico
massa do éster
massa de água
x = 2,26
= (4-x) mols = 1,74 mols = 104,4g
= (3-x) mols = 0,74 mols = 34,0g
= x = 2,26 mols = 198,9 g
= x = 2,26 mols = 40,7 g
Problema 5
Atingido o equilíbrio no problema anterior, foram adicionados ao sistema 60 kg de acetato de
etila; quais serão as quantidades de todas as substâncias presentes no novo equilíbrio?
Equilíbrio
CH3-CH2OH + CH3-COOH  CH3-COO.CH2-CH3 + H2O
0,74 mol/V
1,74 mols/V
2,26 mols/V
2,26mols/V
Adição
+0,68 mols
Novo equilíbrio (0,74+x)/V
(1,74+x)/V
(2,94-x)/V
(2,26-x)/V
Os 0,68 mols de éster adicionados fazem o equilíbrio deslocar para a esquerda. Então x mols
de éster reagem com x mols de água, decrescendo suas concentrações, e produzem mais x
mols de acido e x mols de álcool, aumentando as concentrações destes.
(2,94  x ) (2,26  x )
.
[ester ].[água ]
x 2  5,20.x  6,64
V
V
K4


[alcool ].[ácido ] (0,74  x ) (1,74  x )
x 2  2,48.x  1,29
.
V
V
x2 + 5,04 x - 0,493 = 0
massa de ácido acético
massa de álcool etílico
massa do éster
massa de água
x = 0,096
= (1,74+x) mols = 1,74 mols = 110,4g
= (0,74+x) mols = 0,84 mols = 38,6g
= (2,94-x) mols = 2,84 mols = 249,9 g
= (2,26-x) mols = 2,16 mols = 38,9 g
RESOLUÇÃO DE PROBLEMAS DE EQUILIBRIO ÁCIDO-BASE - CAPÍTULO 4 DA
APOSTILA
Problema 1
Justificar o comportamento ácido-base das espécies químicas indicadas a seguir: HCO3-; CN-;
H2PO4-; HS-, NH3; K+; SO42-; Cl-; PO43-; HBr; CO32-; HCN; HPO42-; Ca2+; NH4+ ; NO3-.
Problema 2
Escrever pares conjugados com as espécies citadas na questão 1.
Problema 3
Dê exemplos de sais que quando em solução só dão origem a espécies apróticas.
Problema 4
Considerando os componentes de um par conjugado, quanto mais forte a constante de
dissociação do ácido mais fraca será a constante de dissociação da base. Deduza a expressão
que pode justificar isso.
Problema 5
Indicar e justificar a natureza das soluções dos seguintes sais: NH4Cl; KCl; KH2PO4; Na2CO3;
Mg2SO4; NaNO3.
Problema 6
Qual a diferença entre as soluções 0,1 mol L-1 de NH4Cl e NH4NO3 quanto ao comportamento
ácido base?
Problema 7
O pH da solução de uma conserva de palmito é 4,16. Calcule a concentração dos íons H+ e
OH- na mesma.
pH = 4,16
pH = log 1/[H+]
pH = - log [H+]
+
-5
-1
[H ]= 6,95 10 mol L
Kw= 10-14 = [H+][OH-]
[OH-] = 10-14/6,92 10-5
-10
-1
[OH ] = 1,44 10 mol L
[H+]= 10 –pH
[H+]=10-4,16
Problema 8
Completar o quadro:
pH
2,5
[H3O+] mol L-1
1,2 10-5
[OH-] mol L-1
pOH
4,3 10-3
4,7
9,3
6,0 10-3
Problema 9
Qual volume de solução 0,25 mol L-1 do ácido forte HCl será necessário para neutralizar 2 L
de solução da base forte NaOH 0,1 mol L-1? E se fosse solução 0,25 mol L-1 do ácido fraco
HAc? Qual seria pH da solução final em cada caso: maior, menor ou igual a 7,0?
Concentração molar = número de mols/Volume em litros de solução
M= n/V
n = M .V
Neutralização de NaOH pelo HCl
2 L solução 0,1 mol L-1 NaOH contem 0,2 mols de NaOH
como HCl + NaOH  NaCl + H2O
serão necessários 0,2 mols de HCl para neutralizar 0,2 mols de NaOH
Em que volume de solução 0,25 mol L-1 HCl estarão os 0,2 mols necessários?
V= n/M, V= 0,2/0,25
V (HCl) = 0,8 L
HCl + NaOH  NaCl + H2O
H+ + Cl- + Na+ + OH-  Na+ + Cl- + H2O
H+ + Cl- + Na+ + OH-  Na+ + Cl- + H2O
H+ + OH-  H2O
O produto da reação efetivamente é apenas H2O e os íons presentes são apróticos. Portanto solução
final é neutra e o pH é 7
Neutralização de NaOH pelo ácido acético (HAc)
HAc + NaOH  NaAc + H2O
serão necessários também 0,2 mols de HAc para neutralizar 0,2 mols de NaOH
Assim serão exigidos também 0,8 L de HAc 0,25 mol L-1
V(HAc)= 0,8 L
HAc + NaOH  NaAc + H2O
HAc + Na+ + OH-  Na+ + Ac- + H2O
HAc + OH-  Ac- + H2O
O produto da reação é H2O e o ânion acetato Ac-, que é uma base. A solução final é alcalina e o pH
>7
Problema 10
Calcular o valor das constantes de equilíbrio das reações a seguir:
NH4+ + H2O  NH3 + H3O+
H2PO4- + H2O  HPO42- + H3O+
CN- + H2O  HCN + OH-
S2- + H2O  HSO4- + OHHCO3- + H2O  CO32- + H3O+
Problema 11
Tem-se 1 L de solução de HCl pH 3,0. Quantos mols de HCl deverão ser neutralizados para
elevar o pH até 4. E para elevar de pH 6 a 7 ?
1 litro solução de HCl pH 3,0
[H+] = 10 –pH = 10 –3 = 0,001 mol L-1
Como o ácido HCl se ioniza totalmente [HCl] = [H+] = 0,001 mol L-1
Em 1 L solução HCl pH 3 tem-se 0,001 mol HCl
Para o pH dessa solução pH 3 se elevar a pH 4, parte do HCl deverá ser neutralizada por
uma base
[H+] = 10 –pH = 10 –4 = 0,0001 mol L-1
[HCl] = [H+] = 0,0001 mol L-1
Em 1 L solução HCl pH 4 tem-se 0,0001 mol HCl
número de mols a serem neutralizados = 0,001 – 0,0001 = 0,0009 mols
n = 0,0009 ou 9 10-4 mols OHPara elevar 1 L de solução de HCl de pH 6 para pH 7 serão necessários 9 10-7 mols OHProblema 12
Uma solução de ácido nítrico 1,6 10-5 mol L-1 tem o mesmo pH de uma solução de ácido
fórmico. Qual a concentração desta última? (Observação: este problema deve ser resolvido
empregando-se a equação quadrática para cálculo de [H3O+]. Qual o erro quando se utiliza a
equação simplificada?
HNO3 é um ácido forte e se dissocia totalmente. Ácido fórmico é um ácido fraco.
Solução 1,6 10-5 mol L-1 HNO3
[HNO3] = [H+] = 1,6 10-5 mol L-1
Como as soluções dos dois ácidos têm o mesmo pH, têm também a mesma concentração de H +
HForm + H2O  H3O+ + Form(Ca-x)
x
x
Ka  1,78.10  4 
x2
Ca  x
x2 + Ka.x + Ka.Ca = 0
x = [H+] = 1,6 10-5
(1,6 10-5)2 + ( 1,78.10  4 . 1,6 10-5) + 1,78.10  4 . Ca = 0
Ca = 1,74 10 –5 mol L-1 de ácido fórmico
Usando a simplificação (Ca-x)  Ca
Ca = 1,44 10-6 mol L-1
Esse resultado é absurdo porque, tendo o mesmo pH, uma solução de ácido fraco não pode ter
concentração menor que a de um ácido forte.
Problema 13
Uma solução 0,12 mol L-1 de ácido acético tem pH 2,84. Qual a constante de dissociação do
ácido acético?
pH = 2,84
Ka 
[H+] = 10 –2,84
[H+] = 1,44 10 –5 mol L-1
x2
1,44.10 5

 1,76.10  5

5
(Ca  x ) (0,12  1,44.10 )
Ka= 1,76 10-5
Problema 14
Transferem-se 25 mL de solução 0,1 mol L-1 de HCl para um balão volumétrico de 100 ml e
completa-se o volume. Pede-se: a concentração de HCl, de H+ , OH- e o pH da solução diluída.
25 ml ou 0,025 L solução HCl 0,1 mol L-1 contem:
n = M .V = 0,025 . 0,1 = 0,0025 mols de HCl
Esse número de mols passará a constituir uma solução cujo volume final será 100 mL ou 0,1 L
Concentração molar = n/V = 0,0025/ 0,1L = 0,025 mol L-1
Após diluição tem-se solução 0,025 mol L-1 HCl
Como o ácido é forte [H+] = [HCl] = 0,025 mol L-1 HCl
pH = log 1/0,025 = 1,60
[OH-] = Kw/[H+] = 10-14/0,025 = 4 10-13 mol L-1
No equilíbrio a concentração de HCl não dissociado é zero
Problema 15
Transferem-se 25 mL de solução 0,1 mol L-1 de acido acético, HAc, para um balão volumétrico
de 100 ml e completa-se o volume. Pede-se: as concentrações no equilibrio de HAc, H+ , OH- e
o pH da solução diluída.
25 mL de HAc 0,1 mol L-1 são diluídos a 100 mL
Como no problema anterior, a solução final diluída terá também concentração 0,025 mol L-1
Neste caso, porém, o ácido é fraco e a constante de ionização Ka será usada no cálculo.
HAc + H2O  H3O+ + Ac(Ca-x)
x
x
Usando a equação simplificada:
[H  ]  Ka.Ca  1,78.10  5.0,025  0,000671 mol L-1
(a resolução pela equação quadrática daria um valor de 0,000658 mol L-1 para [H+])
No equilíbrio: [Ac-] = 0,000671 mol L-1
[HAc] = (Ca-x) = 0,025 – 0,000671 = 0,0243 mol L-1
[OH-] = Kw/[H+] = 10-14/0,000671 = 1,49 10-11 mol L-1
pH = log 1/0,000671 = 3,18
pOH = 14-3,18 = 10,82
Problema 16
Compare os resultados obtidos nos 2 problemas anteriores.
Problema 17
Considerando soluções de mesma concentração das bases CN- e CO32- qual delas tem o pH
mais elevado?
Problema 18
São misturados 25 mL de NaOH 0,45 mol L-1 e 50 mL de HCl 0,12 mol L-1 e o volume é
completado a 500 mL com água destilada. Qual o pH da solução final?
25 mL solução NaOH 0,45 mol L-1 => 0,025L . 0,45 mol L-1 = 0,01125 mols NaOH
50 mL solução HCl 0,12 mol L-1 => 0,050L . 0,12 mol L-1 = 0,00600 mols HCl
Haverá uma reação de neutralização e o volume final a mistura vai ser ajustado a 500 mL :
1 NaOH + 1 HCl  1 NaCl + 1 H2O
0,006 mols de HCl vão reagir com 0,006 mols de NaOH
Assim vão sobrar: 0,01125 - 0,006 = 0,00525 mols de NaOH
A solução final será alcalina e a concentração de NaOH será:
[NaOH] = 0,00525/0,500L = 0,0105 mol L-1 .
Como NaOH é uma base forte:
[OH-] = 0,0105 mol L-1 [H+] = 10-14/ 0,0105 = 9,52 10-13 mol L-1 pH = 12,02
Problema 19
Qual a natureza das soluções aquosas de KH2PO4, K2HPO4, NaHCO3?
Problema 20
Transferem-se 100 mL de solução 1 mol L-1 de NH3 para um balão de 1000 mL. O que poderia
se juntar a esse balão e completar o volume, para se ter uma solução tampão ideal (existem
duas possibilidades, pelo menos)? Qual seria o pH dessa solução?
Problema 21
São transferidos para um balão volumétrico de 500 mL : 20 ml de solução 0,3 mol L-1 de
Na2HPO4 e 50 mL de solução 0,1 mol L-1 de NaH2PO4. Quando o volume for completado com
água destilada qual será o pH da solução?
20 mL solução 0,3 mol L-1 Na2HPO4 => 0,020L . 0,3 mol L-1 = 0,006 mols HPO4-2
50 mL solução 0,1 mol L-1 NaH2PO4 => 0,050L . 0,1 mol L-1 = 0,005 mols H2PO4O volume final é completado a 500 mL; os íons Na+ são apróticos e não participam de equilíbrio
ácido-base e não precisam ser considerados
[HPO4-2] = 0,006/0,5 = 0,012 mol L-1
[H2PO4-] = 0,005/0.5 = 0,010 mol L-1
Trata-se de um sistema tampão que pode ser representado pelo equilíbrio
H2PO4- + H2O  H3O+ + HPO4-2
A constante desse equilíbrio é a segunda constante de ionização do H3PO4
Ka 2  6,2.10
8

[H 3O  ].[ HPO 4  2 ]
[H 2 PO 4  ]
[H 3O  ].0,012

0,010
[H3O+] = 5,17 10-8 mol L-1
pH = 7,29
Problema 22
Indique um par conjugado que poderia ser empregado para se preparar uma solução tampão
que controlasse o pH próximo a 8?
Problema 23
A um balão de 250 mL são adicionados 25 mL de solução 0,12 mol L-1 de ácido acético e 50
mL de solução 0,06 mol L-1 de NaOH, completando-se o volume. Qual o pH da solução
obtida?
20 mL solução 0,12 mol L-1 HAc => 0,020L . 0,12 mol L-1 = 0,003 mols HAc
50 mL solução 0,06 mol L-1 NaOH => 0,050L . 0,06 mol L-1 = 0,003 mols NaOH
O volume final é ajustado a 250 mL
Haverá a reação de neutralização completa
HAc + NaOH  NaAc + H2O
0,003 0,003
0,003
Serão produzidos 0,003 mols de NaAc
[NaAc] = 0,003 mols/0,25L = 0,012 mol L-1
Como Na+ é aprótico interessa considerar que:
[Ac-] = 0,012 mol L-1
Trata-se por tanto do cálculo de pH de uma solução de base fraca. Não é um sistema tampão
porque há predominância apenas de um dos constituintes do par conjugado HAc/Ac -, a base
Ac-
[OH  ]  Kb.Cb  0,012.5,62.10 10  2,60.10  6 mol L-1
[H3O+] = 10-14/2,60 10-6 = 3,85 10-9 mol L-1
pH = log 1/[H+] = 8,41
Problema 24
A um balão de 250 mL são adicionados 25 mL de solução 0,12 mol L -1 de ácido acético e 20
mL de solução 0,07 mol L-1 de NaOH , completando-se o volume. Qual o pH da solução
obtida?
25 mL solução 0,12 mol L-1 HAc => 0,025L . 0,12 mol L-1 = 0,0030 mols HAc
20 mL solução 0,07 mol L-1 NaOH => 0,020L . 0,07 mol L-1 = 0,0014 mols NaOH
O volume final é ajustado a 250 mL
HAc + NaOH  NaAc + H2O
0,0014 0,0014
0,0014
Haverá a reação de neutralização parcial: serão produzidos 0,0014 mols de NaAc e
consumidos 0,0014 mols de HAc. Sobrarão assim 0,0016 mols de HAc
[HAc] = 0,0016mols/0,25L = 0,0064 mols L-1
[Ac-] = 0,0014mols/0,25L = 0,0056 mols L-1
Trata-se de um sistema tampão, pois ocorrem concentrações similares dos dois constituintes
do par conjugado HAc/Ac-. O sistema pode ser representado pela constante de equilíbrio Ka
do ácido acético
Ka  1,78.10
5
[H 3O  ].[ Ac  ] [H 3O  ].0,0056


[HAc ]
0,0064
[H3O+] = 2,03 10-5 mol L-1
pH = 4,69
Problema 25
Qual seria o novo pH da solução obtida no problema 24 se a ela fossem adicionados 2 mL de
solução 0,25 mol L-1 de NaOH? E se fossem 2ml de solução 0,20 mol L-1 de HCl
No preparo da solução do Problema 24 eram produzidos 0,0014 mols de NaAc e sobravam 0,0016
mols de HAc, sendo o volume total 250 mL. Propõe-se agora:
a) adição de 2 mL de NaOH 0,25 mol L-1
Isso corresponde a:
n = 0,002 L . 0,25 mol L-1 = 0,0005 mols de NaOH
Isso causará o consumo de 0,0005 mols de HAc e a produção de mais 0,0005 mols de NaAc
Tem-se agora, portanto: 0,0019 mols de NaAc e 0,0011 mols de HAc
[HAc] = 0,0011mols/0,25L = 0,0044 mols L-1
[Ac-] = 0,0019mols/0,25L = 0,0076 mols L-1
Trata-se ainda de um sistema tampão que pode ser representado pela constante de equilíbrio
Ka do ácido acético
Ka  1,78.10  5 
[H 3O  ].[ Ac  ] [H 3O  ].0,0076

[HAc ]
0,0044
[H3O+] = 1,03 10-5 mol L-1
pH = 4,99
b) adição de 2 mL de HCl 0,25 mol L-1
Isso corresponde a n = 0,002 L . 0,25 mol L-1 = 0,0005 mols de HCl
e causará o consumo de 0,0005 mols de NaAc e a produção de mais 0,0005 mols de HAc
Tem-se agora, portanto: 0,0012 mols de NaAc e 0,0021 mols de HAc
[HAc] = 0,0021mols/0,25L = 0,0084 mols L-1
[Ac-] = 0,0009mols/0,25L = 0,0036 mols L-1
Trata-se ainda de um sistema tampão que pode ser representado pela constante de equilíbrio
Ka do ácido acético
Ka  1,78.10  5 
[H 3O  ].[ Ac  ] [H 3O  ].0,0036

[HAc ]
0,0084
[H3O+] = 4,15 10-5 mol L-1
pH = 4,38
Portanto, a solução tampão teve o pH original de 4,69 aumentado para 4,99 pela adição de
base e abaixado a 4,38 pela adição de acido, demonstrando que o pH da solução resiste a variação.
RESOLUÇÃO DE PROBLEMAS DE EQUILIBRIO PRECIPITACAO-DISSOLUCAO CAPÍTULO 5 DA APOSTILA
Problema 1
O produto de solubilidade do hidróxido de cálcio é 1,3 10-6. Qual será a concentração de íons
Ca2+ e o pH numa solução aquosa saturada de Ca(OH)2?
Ca(OH)2(s)  Ca+2 + 2 OHCada x mols de Ca(OH)2 que se dissolvem por litro produzem x mols/L Ca+2 e 2x mols/L OHKps = 1,3 10-6 = [Ca+2].[OH-]2 = (x).(2x)2 = 4x3
1,3.10
x3
6
 0,00688 mol L-1
4
a solubilidade de Ca(OH)2 é igual a x , ou seja 0,00688 mol L-1
[Ca+2] = x = 0,00688 mol L-1
[OH-] = 2x = 0,0138 mol L-1
[H+]=10-14/0,0138 = 7,25 10-4 mol L-1
pH = 12,14
Problema 2
O produto de solubilidade do sulfato de chumbo é 1,6 10-8. Quais serão as concentrações de
Pb2+ e SO42- quando 1 mol de PbSO4 for adicionado a 1L de água? E se forem 2 moles?
PbSO4(s)  Pb+2 + SO4-2
Cada x mols de PbSO4 que se dissolvem por litro produzem x mols/L Pb+2 e x mols/L SO4-2
Kps = 1,6 10-8 = [Pb+2].[SO4-2] = (x).(x) = x2
x  1,6.10  8  1,26.10  5 mol L-1
Obtém-se uma solução saturada com a dissolução de apenas 1,26 10-5 mol L-1 PbSO4 . Não importa
se forem adicionados 1 ou 2 mols de PbSO4, as concentrações serão sempre:
[Pb+2] = 1,26 10-5 mol L-1
[SO4-2] = 1,26 10-5 mol L-1
Problema 3
Qual o produto de solubilidade do sal Ag2S, sabendo-se que a concentração de prata, Ag+, na
solução saturada desse sal é 6,8 10-7 mol L-1?
Ag2S(s)  2 Ag+ + S-2
Cada x mols de Ag2S que se dissolvem por litro produzem 2x mols/L Ag+ e x mols/L S-2
Kps =[Ag+]2 . [S-2] = (2x)2 . x = 4x3
Kps = 4 . (6,8 10-7)3 = 1,26 10-18
Problema 4
Para saturar 15 ml de água são necessários 0,02 g de BaF2. Qual o produto de solubilidade
desse sal?
BaF2(s)  Ba+2 + 2 FCada x mols de BaF2 que se dissolvem por litro produzem x mols/L Ba+2 e 2x mols/L FKps = [Ba+2].[F-]2 = (x).(2x)2 = 4x3
A solubilidade do sal é fornecida: 0,02 g se dissolvem em 15 mL de água
A massa molar de BaF2 é 175. Portanto 0,02 g de BaF2 ou 0,000114 mols se dissolvem em 0,015 L
de água e a solubilidade x será
0,0076 mol L-1
Kps = 4.(0,0076)3 = 1,77 10-7
Problema 5
Qual a solubilidade do sal Ca3(PO4)2 em água pura e em solução 0,025 mol L-1 CaCl2?
Explique em termos de equilíbrio químico a diferença. Kps Ca3(PO4)2 = 1,0 10-25
Ca3(PO4)2(s)  3Ca+2 + 2 PO4-3
Em água pura, cada x mols de Ca3(PO4)2 que se dissolvem por litro produzem 3x mols/L Ca+2 e 2x
mols/L PO4-2
Kps = 1,0 10-25 = [Ca+2]3.[PO4-3]2 = (3x)3.(2x)2 = 108x5
1,0,10  25
 3,92.10  6 mol L-1
108
Quando o fosfato de cálcio se dissolve na presença de CaCl2 a concentração de cálcio fica nivelada
a 0,025 mol L-1, muito acima da situação anterior.
Kps = 1,0 10-25 = [0,025]3.[PO4-3]2
Como o fosfato é fornecido apenas pelo fosfato de cálcio, ele indica a solubilidade do sal nessa
situação:
Kps = 1,0 10-25 = [0,025]3.[2x]2 = 1,56 10-5 . 4x2
x5
x2
1,0.10  5.
4.1,56.10
5
 4.10 11 mol L-1
Verifica-se portanto que a solubilidade do fosfato de cálcio é bastante restringida na presença
do íon comum Ca+2
Problema 6
Se o pH de uma solução saturada de CaCO3 é 9,95 calcular de modo simplificado o Kps desse
sal. Considerar apenas a primeira ionização do íon CO32CaCO3(s)  Ca+2 + CO3-2
Kps = [Ca+2][CO3-2]
Em água pura, cada x mols de CaCO3 que se dissolvem por litro produzem x mols/L Ca+2 e x
mols/L CO3-2. O íon carbonato atua como base, produzindo íons OH-:
CO3-2 + H2O  HCO3- + OHE indicado que o pH da solução saturada é 9,95, portanto, o pOH é 4,05.
[OH-] = 8,91 10-5 mol L-1
[HCO3-] = 8,91 10-5 mol L-1
Kb1 = 10-14/Ka2 = 10-14/4,7 10-11 = 2,18 10-4
Kb1 
[HCO 3  ][OH  ]
2,18.10  4 
[CO3  2 ]
(8,91.10 5 ) 2
[CO3  2 ]
[CO3-2]= 3,73 10-5 mol L-1
[Ca+2] = [CO3-2] + [HCO3-] = 3,73 10–5 + 8,91 10-5 = 1,26 10-4 mol L-1
Kps = [Ca+2][CO3-2] = (1,26 10–4)(3,73 10-5) = 4,7 10-9
Problema 7
Calcular o pH mínimo para a precipitação de Fe(OH)3 numa solução 10-4 mol L-1 de
Fe2(SO4)3. Kps Fe(OH)3 = 6 10-38.
Fe(OH)3(s)  Fe+3 + 3OHKps = [Fe+3][OH-]3
Solução 10-4 mol L-1 Fe2(SO4)3 é 2 10-4 mol L-1 Fe+3
6 10-38 = (2 10-4)[OH-]3
[OH  ]  3
Fe+3
Para a concentração de
mol L-1. Isso corresponde a:
6.10  38
4
 6,64.10 12 mol L-1
2.10
dada, a concentração mínima necessária de íon OH- é 6,64 10-12
pOH = 11,17 e pH = 2,83
Problema 8
500 mL de uma solução 0,4 mol L-1 Na2SO4 foram misturadas a 500 mL de uma solução 0,2
mol L-1 CaCl2. Calcular as concentrações dos íons em equilíbrio e massa de precipitado
formado. Kps CaSO4 = 2,5 10-5
número de mols de Na2SO4 = 0,5 L . 0,4 mol L-1 = 0,2
número de mols de CaCl2 = 0,5 L . 0,2 mol L-1 = 0,1
Volume final total = 1000mL
Na2SO4 + CaCl2  2 NaCl + CaSO4
0,1 mols de CaCl2 reagem com 0,1 mols de Na2SO4 formando 0,1 mol de CaSO4 que se
precipita. Sobrarão ainda 0,1 mol de Na2SO4 que estão em excesso. O sistema final
corresponderá então à fase sólida CaSO4 na presença do íon comum SO4-2 no volume de 1000
mL.
A massa de CaSO4 é 0,1 mol ou seja:
0,1 . 136 = 13,6 g
A concentração de íon sulfato será
[SO4-2] = 0,1 mol L-1
CaSO4(s)  Ca+2 + SO4-2
Cada x mols de CaSO4 que se dissolvem por litro produzem x mols/L Ca+2 e x mols/L SO4-2,
mas aqui a concentração de sulfato é aumentada bastante pelo sulfato em excesso.
Kps = 2,5 10-5 = [Ca+2].[SO4-2] = [Ca+2].(0,1)
[Ca+2] = 2,5 10-4 mol L-1
Problema 9
Uma solução de íons Cd2+ na concentração de 0,01 mol L-1 tem seu pH ajustado para 8,85.
Pergunta-se se haverá ou não precipitação de Cd(OH)2, cujo Kps é 2 10-14.
Cd(OH)2(s)  Cd+2 + 2OHKps = [Cd+2][OH-]
[Cd+2] = 0,01 mol L-1
pH = 8,85 pOH =5,15 [OH-] = 7,08 10-6 mol L-1
Q = 0,01. (7,08 10-6 )2 = 5,01 10-13
Como o produto dos íons Q é superior ao Kps, o hidróxido de cádmio irá precipitar.
Problema 10
Calcular a solubilidade do Mg(OH)2 em água pura e em solução pH 12. Kps Mg(OH)2 = 1,8
10-11.
Mg(OH)2(s)  Mg+2 + 2 OHEm água pura, cada x mols de Mg(OH)2 que se dissolvem por litro produzem x mols/L Mg+2 e x
mols/L OHKps = 1,8 10-11 = [Mg+2].[OH-]2 = (x).(2x)2 = 4x3
1,8.10 11
 0,000165 mol L-1
4
a solubilidade de Mg(OH)2 em água pura é igual a x , ou seja 0,000165 mol L-1
x3
Sob pH 12, ou pOH 2, a concentração de OH- será 0,01 mol L-1. Assim no equilíbrio de dissolução
a pH 12, a concentração de OH- é elevada a um nível muito superior aquele da dissolução do
hidróxido de magnésio em água.
Nessa condição a solubilidade do sal será indicada pela concentração de Mg+2:
Kps = 1,8 10-11 = [Mg+2].(0,01)2
[Mg+2] = 1,8 10-11/10-4 = 1,8 10-7 mol L-1
RESOLUÇÃO DE PROBLEMAS DE EQUILÍBRIO DE COMPLEXAÇÃO - CAPÍTULO 6
DA APOSTILA
Problema 1
O que caracteriza um ligante? O que diferencia o quelato de um complexo?
Problema 2
Quando amônia é adicionada a solução de sulfato cúprico 0,2 mol L -1, a cor azul celeste desta
muda para uma cor azul profundo do íon complexo Cu(NH 3)42+. Se a concentração de NH3
livre no equilíbrio é 0,1 mol L-1 , a do íon complexo Cu(NH3)42+ corresponde a 92,97% de
todas as espécies contendo cobre. Calcular a concentração das espécies: Cu2+; Cu(NH3)2+;
Cu(NH3)22+ e Cu(NH3)32+. Para obter as constantes necessárias consulte o texto.
A concentração de Cu+2 dissolvida inicialmente é 0,2 mol L-1
Todas as formas de cobre presente na solução se originam deste teor inicial. Portanto:
[Cu2+] + [Cu(NH3)2+] + [Cu(NH3)22+] + [Cu(NH3)32+] + [Cu(NH3)42+] = 0,2 mol L-1
Cu2+ + NH3
Cu(NH3)2+ + NH3
Cu(NH3)22+ + NH3
Cu(NH3)32+ + NH3
Cu2+ + 4 NH3
 Cu(NH3)2+
 Cu(NH3)22+
 Cu(NH3)32+
 Cu(NH3)42+
 Cu(NH3)42+
K1 = 1,41 104
K2 = 3,16 103
K3 = 7,76 102
K4 = 1,35 102
K = 4,68 1012
Informa-se que [NH3] no equilíbrio é 0,1 mol L-1 e que [Cu(NH3)42+] é 92,97% de 0,2 mol L-1 ou
seja:
[Cu(NH3)42+] = 0,18594 mol L-1
[Cu( NH3 ) 4 ]
K
[Cu
2
][ NH3 ]
4
4,68.1012 
0,18594
[Cu
2
](0,1)
4
[Cu+2] = 3,97 10-13 mol L-1
K4 
[Cu( NH3 ) 4 ]
[Cu( NH3 ) 3 ].[ NH3 ]
1,35.10 2 
0,18594
[Cu( NH3 ) 3 ].(0,1)
[Cu(NH3)3] = 0,0138 mol L-1
K3 
[Cu( NH3 )3]
[Cu( NH3 ) 2 ].[ NH3 ]
1,35.10 2 
0,0138
[Cu ( NH 3 ) 2 ].(0,1)
[Cu(NH3)2] = 0,000177 mol L-1
K2 
[Cu( NH3 ) 2 ]
[Cu( NH3 )].[ NH3 ]
3,16.10 3 
0,000177
[Cu ( NH 3 )].( 0,1)
[Cu(NH3)] = 5,62 10-7 mol L-1
Problema 3
As complexações de Zn2+ e Mg2+ pelo EDTA são representadas pelas equações:
Zn2+ + Y4-  [ZnY]2K est = 3,2 1016
Mg2+ + Y4-  [MgY]2K est = 4,9 108
Duas séries de volumes de 100 mL de solução de EDTA 0,12 mol L-1 foram ajustadas a valores
de pH 2, 4 e 6. Aos 3 volumes de uma série foram adicionados 1,2 milimols de Zn2+ e a outra
1,2 milimols de Mg2+. Calcular as concentrações das formas livre e complexada de zinco e de
magnésio nas soluções citadas, sabendo-se que as concentrações da forma desprotonada do
EDTA, Y4-, naqueles valores de pH são:
pH
[Y4-] mol L-1
2
4,4 10-15
4
4,0 10-10
6
2,6 10-6
Complexo ZnEDTA
[Zn+2] total = 0,012 mol L-1
[Zn+2] + [ZnY] = 0,012
[ ZnY ]
Kest 
[ Zn
2
].[ Y  4 ]
pH 2
(0,012  x )
Kest  3,2.1016 
( x ) . 4,4.10
15
x = [Zn+2] = 8,46 10-5
[ZnY] = 1,19 10-2 mol L-1
pH 4
[Y4-] = 4,0 10-10 mol L-1
x = [Zn+2] = 9,37 10-10
[ZnY] = 0,012 mol L-1
pH 6
[Y4-] = 2,6 10-6 mol L-1
x = [Zn+2] = 1,44 10-13
[ZnY] = 0,012 mol L-1
Complexo MgEDTA
[Mg+2] total = 0,012 mol L-1
[Mg+2] + [MgY] = 0,012
Kest 
[MgY ]
[Mg  2 ].[ Y  4 ]
pH 2
Kest  4,9.108 
(0,012  x )
( x ) . 4,4.10
x = [Mg+2] = 0,0111999
15
pH 4
[Y4-] = 4,0 10-10 mol L-1
x = [Mg+2] = 0,010033
pH 6
[Y4-] = 2,6 10-6 mol L-1
x = [Mg+2] = 9,41 10-6
[MgY] = 2,59 10-8 mol L-1
[MgY] = 1,96 10-3 mol L-1
[ZnY] = 0,011990 mol L-1
Problema 4
Qual a concentração de prata em gramas de prata por litro em uma solução que é 0,01 mol L -1
em [Ag(CN)2]-, sabendo-se que a constante de estabilidade do íon dicianoargentato é 1,0 1021?
Ag = 108
Ag+ + 2CN-  [Ag(CN)2]x
2x  (0,01-x)
Kest  1,0.10 21 
[Ag (CN) 2 ]
[Ag  ].[CN  ]2

(0,01  x )
( x )( 2x ) 2
Como o complexo de dissocia muito pouco para simplificar considera-se que :
(0,01 – x) = 0,01
x3
0,01
21
 1,36.10 8 mol L-1
4.10
[Ag+] = 1,36 10-8 . 107 = 1,45 10-6 g L-1
Problema 5
O cátion Zn2+ forma complexos com o íon cianeto e a amônia. Calcule qual a concentração de
íons Zn2+ que permanece livre em uma solução 0,02 mol L-1 de íon tetracianozincato e em
outra solução que é 0,02 mol L-1 em íon tetramimozinco. Com base no resultados obtidos
esclareça qual dos ligantes é mais efetivo na complexação de zinco. Dados: Kest [Zn(CN)4]- =
1019 e Kest [Zn(NH3)4]2+ = 1014.
Complexação do zinco com cianeto
Zn+2 + 4 CN-  [Zn(CN)4]-2
Kest  1.1019 
[ Zn (CN) 4 ]
[ Zn
2
 4

][CN ]
(0,02  x )
( x )( 4x ) 4
Como o complexo de dissocia muito pouco para simplificar considera-se que :
(0,02 – x) = 0,02
[ Zn  2 ]  x  5
0,02
19
= 2,39 10–5 mol L-1
256.10
na complexação com NH3 repete-se exatamente o mesmo esquema, apenas usando a constante
apropriada.
[ Zn  2 ]  x  5
0,02
14
 2,39 10-4 mol L-1
256.10
O íon cianeto é mais eficiente em complexar o Zn que a amônia, por isso a concentração de
zinco é menor na presença dele.
Problema 6
Analisar a ação do EDTA sobre os hidróxidos de Fe3+ e Ni2+, expressa pelas equações:
Fe(OH)3(s) + EDTA  [Fe-EDTA] + 3OHNi(OH)2 (s) + EDTA  [Ni-EDTA] + 2OHDados: K est [Fe-EDTA] = 1,26 1025
K est [Ni-EDTA] = 3,98 1018
Kps Fe(OH)3 = 3 10-38
Kps Ni(OH)2 = 6,5 10-18
A dissolução do hidróxido férrico pelo EDTA será governada pela constante:
K
[FeEDTA ].[OH  ]3
[EDTA ]
A constante procurada pode ser obtida em função das constantes Kest e Kps fornecidas:
K
[FeEDTA ].[OH  ]3 [Fe 3 ]
[FeEDTA ]
.

. [Fe  3 ].[OH  ]3  Kest . Kps
3
3
[EDTA ]
[Fe ] [EDTA ].[ Fe ]
K = 1,26 1025 . 3 10-38 = 3,78 10-13
Idêntico procedimento é aplicado à dissolução do hidróxido de níquel pelo EDTA:
K= 3,98 1018 . 6,5 10-18 = 25,87
O EDTA dissolve Ni(OH)2 mas não Fe(OH)3 conforme mostram as constantes de cada reação.
RESOLUÇÃO DE PROBLEMAS DE EQUILÍBRIO DE OXIDAÇÃO-REDUÇÃO CAPÍTULO 7 DA APOSTILA
Problema 1
Calcule o número de oxidação dos elementos indicados nos seguintes compostos:; Na2CrO4;
SO3; SO2; Cl2; Na4P2O7; C6H12O6; K2Cr2O7; CO32-; Na2S4O6, KMnO4; O3; O2; CO2; CO.
Problema 2
O nitrogênio se apresenta sob diferentes números de oxidação em espécies como: N2O3, N2O5,
NH3; NH4+, N2O, CH3-NH2, N2, NO2-. Escreva-as em ordem crescente de número de oxidação.
Problema 3
O que acontecerá com as lâminas metálicas mostradas a seguir, quando imersas nas soluções
contendo os íons indicados?
Cu
I- Ag+(aq)
Cu
II-Zn2+(aq)
Zn
III-Cu2+(aq)
Fe
IV-Cu2+(aq)
Ag
V-Fe2+(aq)
I-Prata é reduzida.
Cu+2 + 2e-  Cu0 o = 0,34 V
Ag+ + E-  Ag0
o = 0,80 V
o
Para se ter  positivo para a reação global, a semireacao do Cu deve ser invertida
Reação espontânea: Cu0 + 2 Ag+  Cu+2 + 2Ag0 o = 0,46V
II- Nada ocorre: cobre metálico não será oxidado pelo íon Zn+2
III- Oxidação do zinco metálico. Reação espontânea: Zn0 + Cu+2 Cu0 + Zn+2
IV- Ferro é oxidado. Reação espontânea: Fe0 + Cu+2 Cu0 + Fe+2
V- Nada ocorre. A prata metálica não será oxidada
Problema 4
Uma célula eletroquímica é formada por eletrodos:
Ag(s)/Ag+(aq, 0,2 mol L-1)
Cd(s)/Cd2+(aq, 0,32 mol L-1)
Representar esquematicamente essa célula; indicar catodo e ânodo, o sentido do movimento
dos elétrons; calcular o potencial e balancear a reação química que ocorre espontaneamente
na célula.
Ag+ + e-  Ago
o = 0,800 V
Cd+2 + 2e-  Cdo o = -0,402 V
Para se ter o positivo para a reação global, a semireacao do Cd deve ser invertida
Reação espontânea: Cd0 + 2 Ag+  Cd+2 + 2Ag0 o = 1,202 V
   o 
0,0592
[Cd 2 ]
. log
n
[Ag  ]2
   o 
0,0592
0,32
= 1,175 V
. log
2
(0,20) 2
Anodo é o eletrodo onde ocorre oxidação: Cdo Cd+2 + 2eCatodo é o eletrodo onde ocorre a redução: Ag+ + e-  Ago
Problema 5
A determinação de carbono orgânico em diferentes matrizes pode ser conduzida por reação
com íon dicromato em meio ácido:
K2Cr2 O7 + C6H12O6 + H2SO4  Cr2(SO4)3 + K2SO4 + CO2 + H2O
Pede-se para: balancear a equação química, indicar quem é o agente oxidante, quem é o
agente redutor. Mostre que o íon Cl- também pode reagir com o dicromato, sendo por isso
mesmo um interferente na determinação do carbono orgânico.
Problema 6
A corrosão do ferro metálico é uma reação de oxidação-redução, forma-se uma célula
galvânica onde o ferro atua como anodo:
2Fe(s) + O2 + H2O  Fe2+ + 2OHPara evitar a corrosão usa-se aço galvanizado, recobrindo o ferro com uma película de zinco.
Explique esse processo em termos de uma reação de oxidação redução.
Problema 7
Mostre que a constante de equilíbrio da reação abaixo é 3 1011.
Cu2+(aq) + H2(g)  Cu0 + 2 H+(aq)
Problema 8
Em uma célula galvânica cobre-prata mediu-se o potencial obtendo-se 0,433 Volts. Qual a
concentração do íon Cu2+ se a concentração de Ag+ é 0,12 mol L-1?