ExHinfinito - SEL (EESC/USP)

Exercícios propostos: Controle H-inf
SEL 380 Controle Robusto
Profa. Vilma A.Oliveira
Abril 2002
Problema 1.
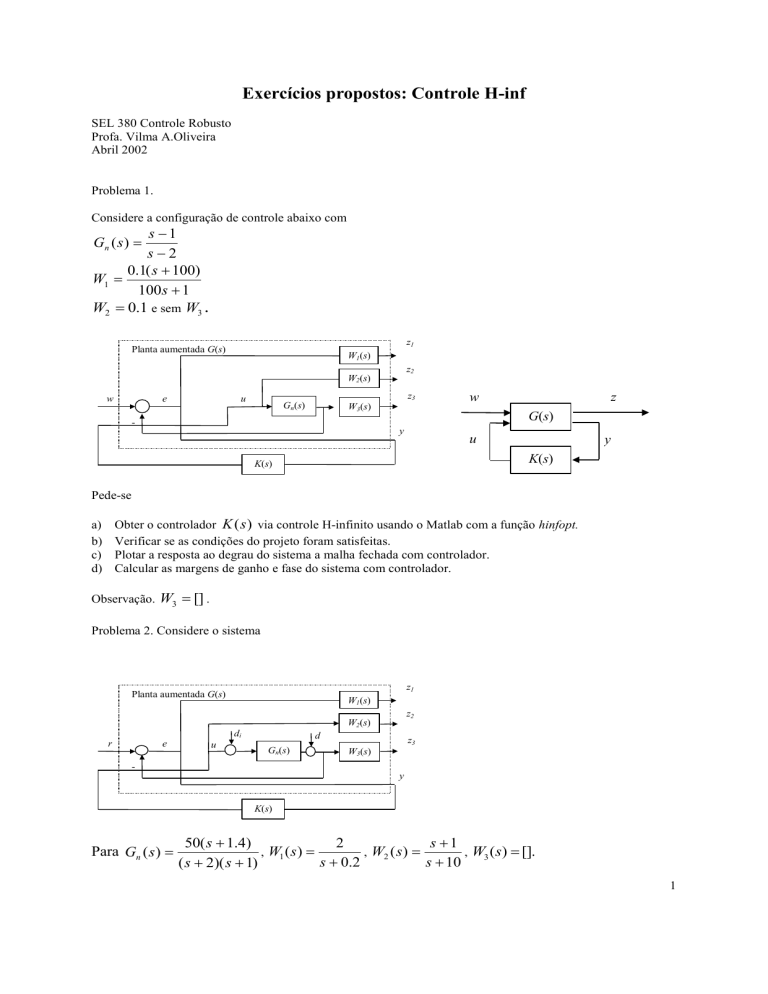
Considere a configuração de controle abaixo com
s 1
s2
0.1( s  100)
W1 
100s  1
W2  0.1 e sem W3 .
Gn ( s ) 
z1
Planta aumentada G(s)
W1(s)
z2
W2(s)
w
e
z3
u
Gn(s)
W3(s)
w
z
G(s)
y
u
y
K(s)
K(s)
Pede-se
Obter o controlador K (s ) via controle H-infinito usando o Matlab com a função hinfopt.
Verificar se as condições do projeto foram satisfeitas.
Plotar a resposta ao degrau do sistema a malha fechada com controlador.
Calcular as margens de ganho e fase do sistema com controlador.
a)
b)
c)
d)
Observação.
W3  [] .
Problema 2. Considere o sistema
z1
Planta aumentada G(s)
W1(s)
z2
W2(s)
di
r
e
u
d
Gn(s)
z3
W3(s)
y
K(s)
Para Gn ( s ) 
s 1
2
50( s  1.4)
, W1 ( s ) 
, W2 ( s ) 
, W3 ( s)  [].
s  0.2
s  10
( s  2)( s  1)
1
d 
z 
w    e z   1  seja minimizada. Na forma de
 z2 
d i 
d 
 z1 
LFT a função de transferência a ser minimizada é dada por    Tzw   . Fornecer o valor do gama
 z2 
d i 
Projetar um controlador tal que a norma H-infinito entre
encontrado via hinfopt.
Para gerar o sistema aumentado (2 blocos) em malha aberta utiliza-se a sintaxe do comando sysic do Toolbox
MU do Matlab conforme rotina abaixo. Utilizar ltisys('tf',num,den) para entrar as variáveis Gn, W1 e W2.
systemnames='Gn W2 W1'; %define o nome das variáveis do sistema
inputvar='[di; d; u]'; %define as variáveis de entrada no sistema
outputvar='[W2 ; W1; Gn + d]'; %define as variáveis de saída do sistema
input_to_Gn='[u + di]';%define as variáveis de entrada na planta Gn
input_to_W2='[u]'; %define as variáveis de entrada em W2
input_to_W1='[Gn + d]'; %define as variáveis de entrada em W1
sysoutname='G'; %atribui um nome para o sistema interconectado
cleanupsysic='yes'; % limpa as variáveis geradas anteriormente por sysic
sysic %gera a matriz de sistema aumentado (interconectado)
di
W2(s)
u
d
Gn(s)
W1(s)
y
2