Lista de Exercícios Extra- Relações Métricas Prof. Marcia 9º Ano

Lista de Exercícios Matemática – 1º. EM
Polígonos e Função de 2º. Grau
O vértice da parábola será voltado para cima (neste caso o vértice é chamado de ponto de mínimo) se o número
com o X2 for positivo e será voltado para baixo (neste caso o vértice é chamado de ponto de máximo) se este
número for negativo.
O Zero da Função ou Raiz, nos indica que devemos pegar a função igualar a Zero e determinar o(s) valor(es) de
X, que a tornam igual a Zero.
V(Xv, Yv) => Xv = -b/2a
Si = (n – 2) * 180° D = n(n-3)/2
e Yv = -/4a
Ai = Si / n
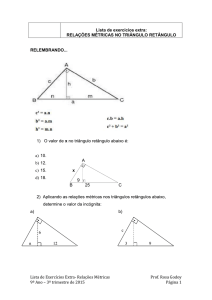
1ª.) Determine a medida dos ângulos indicados:
a)
b)
Lista de Exercícios Extra- Relações Métricas
9º Ano – 3º trimestre de 2012
Prof. Marcia
Página 1
c)
d) As medidas dos ângulos internos de um quadrilátero são: x + 17° ; x + 37° ; x + 45°
e x + 13°. Determine as medidas desses ângulos.
e) No paralelogramo abaixo, determine as medidas de x e y.
f) A figura abaixo é um losango. Determine o valor de x e y, a medida da diagonal
, da diagonal
e o perímetro do triângulo BMC.
g) No retângulo abaixo, determine as medidas de x e y indicadas:
Lista de Exercícios Extra- Relações Métricas
9º Ano – 3º trimestre de 2012
Prof. Marcia
Página 2
h) Determine as medidas dos quatro ângulos do trapézio da figura abaixo:
2ª.) Determine o número de diagonais dos polígonos de 10, 15, 20, 30 e 40 lados.
Função Quadrática
Definição
Chama-se função quadrática, ou função polinomial do 2º grau, qualquer função f de IR em IR dada por uma
lei da forma f(x) = ax2 + bx + c, onde a, b e c são números reais e a 0.
Vejamos alguns exemplos de função quadráticas:
1.
2.
3.
4.
5.
f(x) = 3x2 - 4x + 1, onde a = 3, b = - 4 e c = 1
f(x) = x2 -1, onde a = 1, b = 0 e c = -1
f(x) = 2x2 + 3x + 5, onde a = 2, b = 3 e c = 5
f(x) = - x2 + 8x, onde a = -1, b = 8 e c = 0
f(x) = -4x2, onde a = - 4, b = 0 e c = 0
Gráfico
O gráfico de uma função polinomial do 2º grau, y = ax2 + bx + c, com a 0, é uma curva
chamadaparábola.
Exemplo:
Vamos construir o gráfico da função y = x2 + x:
Primeiro atribuímos a x alguns valores, depois calculamos o valor correspondente de y e, em seguida,
ligamos os pontos assim obtidos.
Lista de Exercícios Extra- Relações Métricas
9º Ano – 3º trimestre de 2012
Prof. Marcia
Página 3
x
y
-3
6
-2
2
-1
0
0
0
1
2
2
6
Observação:
Ao construir o gráfico de uma função quadrática y = ax2 + bx + c, notaremos sempre que:
 se a > 0, a parábola tem a concavidade voltada para cima;
 se a < 0, a parábola tem a concavidade voltada para baixo;
Zero e Equação do 2º Grau
Chama-se zeros ou raízes da função polinomial do 2º grau f(x) = ax2 + bx + c , a 0, os números reais x
tais que f(x) = 0.
Então as raízes da função f(x) = ax2 + bx + c são as soluções da equação do 2º grau ax2 + bx + c = 0, as
quais são dadas pela chamada fórmula de Bhaskara:
Temos:
Observação
A quantidade de raízes reais de uma função quadrática depende do valor obtido para o
radicando
 quando
 quando
 quando
, chamado discriminante, a saber:
é positivo, há duas raízes reais e distintas;
é zero, há só uma raiz real (para ser mais preciso, há duas raízes iguais);
é negativo, não há raiz real.
1º.) Fazer o gráfico das funções abaixo:
y = x2 - 3x + 2
y = -x2 + 6x – 8
y = x2
y = -x2
2º.) Dada a função quadrática f(x) = 3x² - 4x + 1, determine:
a) f(1)
b) f(0)
c) f( 2 )
d) f(-2)
e) f(h + 1)
f) x de modo que f(x) = -1
3º.) Determine, se existirem, os zeros das funções quadráticas abaixo:
a) f(x) = x² - 3x
c) f(x) = -x² +2x + 8
b) f(x) = x² +4x + 5
d) –x² +3x – 5
4º.) Para que valores reais de k a função f(x) = (k - 1)x² - 2x + 4 não admite zeros reais?
Lista de Exercícios Extra- Relações Métricas
9º Ano – 3º trimestre de 2012
Prof. Marcia
Página 4
5º.) Vamos estudar os sinais das seguintes funções:
a) f(x) = x² - 7x + 6
b) f(x) = 9x² + 6x + 1
c) f(x) = -2x² +3x – 4
6º.) Em um terreno, na forma de um triângulo retângulo, será construído um jardim retangular, conforme figura abaixo.
Sabendo-se que os dois menores lados do terreno medem 9 m e 4 m, as dimensões do jardim para que ele tenha a maior
área possível, serão, respectivamente, (utilize semelhança de triângulos)
a) 2,0 m e 4,5 m.
b) 3,0 m e 4,0 m.
c) 3,5 m e 5,0 m.
d) 2,5 m e 7,0 m.
INEQUAÇÕES
1. Resolva as inequações U = R
a) 8x – 10 > 2x + 8
b) 2(3x +7) < – 4x + 8
c) 20 – (2x +5) ≤ 11 + 8x
2. Resolva as inequações U = N
a) 2x + 5 < – 3x +40
b) 6(x – 5) – 2(4x +2) > 100
c) 7x – 9 < 2x + 16
3. Resolva as inequações U = Z
a) 2x + 5 ≥ – 3x +40
c) 20 – (7x + 4) < 30
b) 6(x – 5) – 2(4x +2) ≥ 80
4. Resolva as inequações em R:
2x  1
0
a) x  2
x 1
0
b) x  1
2x  3
0
c) x  2
d)
1
2

e) x  1 x  2
h)
x  1. x  2  0
x  3. x  4
i) (5 x  2).( 2  x ).( 4 x  3)  0
2x  7
3
f) 3x  5
5. (UFRS) Se –1< 2x + 3 <1, então 2 – x está entre:
a) 1 e 3
b) –1 e 0
c) 0 e 1
6. (UNAERP) Se 3  5 – 2x  7, então:
a) -1  x  1
b) 1  x  -1
3x  1
3
g) x  2
1  2x . 3  4x   0
4  x 
d) 1 e 2
c) -1  x  1
e) 3 e 4
d) x = 1
e) x = 0
7. (PUC) Fábio quer arrumar um emprego de modo que, do total do salário que receber, possa gastar 1/4 com alimentação, 2/5 com
aluguel e R$ 300,00 em roupas e lazer. Se, descontadas todas essas despesas, ele ainda pretende que lhe sobrem no mínimo R$
85,00, então, para que suas pretensões sejam atendidas, seu salário deve ser no mínimo:
a) R$ 950,00
b) R$ 1100,00
c) R$ 980,00
d) R$ 1500,00
e) R$ 1000,00
Lista de Exercícios Extra- Relações Métricas
9º Ano – 3º trimestre de 2012
Prof. Marcia
Página 5
8. (FUVEST) Um estacionamento cobra R$6,00 pela primeira hora de uso, R$3,00 por hora adicional e tem uma despesa diária de
R$320,00. Considere-se um dia em que sejam cobradas, no total, 80 horas de estacionamento. O número mínimo de usuários
necessário para que o estacionamento obtenha lucro nesse dia é:
a) 25
b) 26
c) 27
d) 28
e) 29
9. (UNESP) Carlos trabalha como DJ e cobra uma taxa fixa de R$100,00, mais R$20,00 por hora, para animar uma festa. Daniel, na
mesma função, cobra uma taxa fixa de R$55,00, mais R$35,00 por hora. O tempo máximo de duração de uma festa, para que a
contratação de Daniel não fique mais cara que a de Carlos, é:
a) 6 horas
b) 5 horas
c) 4 horas
d) 3 horas
e) 2 horas
10. (UNICAMP) Três planos de telefonia celular são apresentados na tabela abaixo:
PLANO
A
B
C
CUSTO FIXO MENSAL
R$ 35,00
R$ 20,00
0
CUSTO ADICIONAL POR MINUTO
R$ 0,50
R$ 0,80
R$ 1,20
a) Qual é o plano mais vantajoso para alguém que utilize 25 minutos por mês?
b) A partir de quantos minutos de uso mensal o plano A é mais vantajoso que os outros dois?
Respostas: 1) a) S = {x R / x > 3}; b) S = {xR / x < - 3/5}; c) S = { x  R / x ≥ 2/5};
2) a) S = {0, 1, 2, 3, 4, 5, 6}; b) S = Φ; c) S = {0,1, 2, 3, 4}; 3) a) S = {7, 8, 9, 10,...}; b) S = {...,-59, -58, -57};
c) S = {-1, 0, 1, 2, ...}; 4) a) ]-∞, -2[  ]-1/2, +∞[; b) ]-1, 1[; c) ]-2, 3/2]; d) ]-3/4, 1/2[  ]4, +∞[; e) ]0, 1[  ]2, +∞[;
f) [8/7, 5/3[; g) ]- ∞, 2[; h) ]-4, -3[  [1, 2]; i) ]-∞, -3/4]  [-2/5, 2]; 5) e; 6) a; 7) b; 8) c; 9
Lista de Exercícios Extra- Relações Métricas
9º Ano – 3º trimestre de 2012
Prof. Marcia
Página 6