COMPUTAÇÃO GRÁFICA – 135L

COMPUTAÇÃO GRÁFICA
MÓDULO 1:
Visão geral. Conceituação e terminologia.






Computação Gráfica. Definição, áreas de atuação e mercado de trabalho.
Arquitetura de sistemas gráficos (o hardware gráfico).
Primitivas como elementos básicos do desenho (pontos, retas, polilinhas, circunferências e
elipses).
Primitivas com funções de linguagem (setWindows(), getPixel(), ...).
Renderização e rasterização.
Pacotes gráficos e bibliotecas principais (OpenGL e DirectX).
Presente em diversos segmentos da atividade humana, como nas artes, na medicina, arquitetura,
segurança pública, propaganda, processamento de dados, lazer, educação, etc. a Computação
Gráfica (CG) é a área da Ciência da Computação que mobiliza os recursos matemáticos para gerar,
manipular e interpretar imagens com a ajuda do computador. Praticamente tudo que poderíamos
realizar usando imagens por meios tradicionais pode ser tratado mais rápida e eficientemente com a
CG.
Na medicina, por exemplo, o emprego de scanners para a sondagem de órgãos internos sem
intervenção cirúrgica tornou o diagnóstico de doenças mais seguro e precoce. O uso de ferramentas
de CAD/CAM (Computer-Aided Design/Computer-Aided Manufacturing) possibilitam arquitetos e
engenheiros elaborarem projetos de estruturas mais arrojadas e complexas, com cálculos mais
precisos e visualização prévia dos resultados antes mesmos que estes sejam executados, permitindo
avaliações mais seguras e rápidas.
Embora o domínio da tecnologia da CG não faça do indivíduo um artista, um médico, ou arquiteto,
nas mãos de tais profissionais, seu domínio pode levar o sujeito à dimensões inimagináveis
anteriormente.
Já para o cientista da computação, engenheiro, ou o analista de sistemas de informação a CG pode
ser vista como um fim em si. Ou seja, cabe a esses profissionais o desenvolvimento e a integração
das ferramentas que virão a ser utilizadas por outros profissionais no desenvolvimento de seus
produtos.
Sendo uma das grandes área da Ciência da Computação podemos subdividir a Computação Gráfica,
didaticamente, em três subáreas a saber:



Síntese de Imagens
Processamento (Manipulação) de Imagens
Análise de Imagens (Visão Computacional)
Cada uma dessas subáreas, embora interligadas e, muitas vezes, sobrepostas, goza de certa
independência das demais, requerendo o desenvolvimento de competências específicas.
Na SÍNTESE DE IMAGENS consideramos as representações visuais de objetos criados pelo
computador a partir de especificações geométricas e visuais de seus componentes, ou seja, da
representação gráfica da informação. Exemplos: elaboração de um gráfico representativo da
distribuição de freqüências de um determinado evento registrado em uma planilha, o registro digital
de uma imagem por meio de um scanner ou câmera, a criação de imagem de uma cena para um
filme de animação.
O PROCESSAMENTO DE IMAGENS considera o tratamento da imagem em sua forma digital, suas
transformações e melhoramentos. Exemplos: A restauração de uma fotografia antiga utilizando
1
meios digitais, o realce de detalhes de uma imagem de uma câmera de segurança, a vetorização de
uma imagem cartográfica (isso já não seria objeto da área de análise?).
Já a ANÁLISE DE IMAGENS considera a especificação dos componentes da imagem a partir de sua
representação visual. Exemplos: o reconhecimento de caracteres em um texto digitalizado (OCR –
Optical Character Recognition), o estudo de manchas urbanas, áreas de desmatamento,
levantamento topográfico, etc. ... a partir de imagens de satélite ou aerofotogrametria.
Assim, podemos definir a Computação Gráfica de várias maneiras, mais ou menos abrangentes:
"Computação Gráfica é a área da Ciência da Computação que trata a geração,
manipulação e interpretação de modelos matemáticos, na forma de imagens, utilizando
o computador."
"A Computação Gráfica consiste no conjunto de métodos e técnicas de converter dados
para um dispositivo gráfico, via computador."
“A computação gráfica é a área da ciência da computação que estuda a transformação
dos dados em imagem. Esta aplicação estende-se à recriação visual do mundo real por
intermédio de fórmulas matemáticas e algoritmos complexos.” <pt.wikipedia.org>
Observe a maior ou menor abrangência de cada uma das tentativas de definirmos Computação
Gráfica e tente elaborar a sua própria. O importante é compreender Computação Gráfica como uma
área de desenvolvimento e pesquisa de uma ciência maior, a Ciência da Computação.
O Conceito de Primitivas Gráficas
Chamamos de primitivas gráficas os elementos básicos de gráficos/desenhos a partir dos quais são
construídos outros objetos, mais complexos, mas também entram na definição de primitivas os
comandos e funções que manipulam e alteram os elementos gráficos de uma imagem.
Conforme a primeira definição de primitiva gráficas podemos exemplificar as primitivas como:


Em 2D: pontos, linhas, polilinhas, retângulos, circunferência, elipse, etc. ...
Em 3D: planos, caixas, esferóides, cilindros, cones, etc. ...
Mas também servem como exemplos de primitivas gráficas funções como:


Em 2D: WritePixel(x,y,cor), cor = GetColor(x,y), Form1.Canvas.Pixel[x,y]:=RGB(r,g,b)
Em 3D: plane{ y,0 texture{pigment{color rgb <r,g,b>}}}}
Rasterização e Renderização
Dois termos muito empregados em Computação Gráfica e Processamento de Imagens são
RASTERIZAÇÃO (rastering) e RENDERIZAÇÃO (rendering). Na Wikipédia (pt.wikipedia.org)
encontramos definições bastante simples para ambos:
i. Rasterização, é a tarefa de tomar uma imagem descrita vetorialmente e convertê-la em uma
imagem raster (matriz de pixel) para a saída em vídeo ou impressora.
ii. Renderização é o processo pelo qual se pode obter o produto final de um processamento digital
qualquer.
2
MÓDULO 2.
Mapeamento window-to-viewport




Pontos, vetores e matrizes em CG.
Sistemas de referência (universo, dispositivo, objeto e normalizado).
A janela de visualização (viewport) e recorte (clipping).
Mapeamento de pontos (pixels) na janela de visualização (Mapeamento window-to-viewport).
Primitivas Gráficas em 2D
Como dito no módulo anterior, primitivas gráficas são ambos elementos básicos de
gráficos/desenhos, a partir dos quais são construídos outros objetos, mais complexos, e também os
comandos e funções que manipulam e alteram os elementos gráficos de uma imagem.
No que diz respeito à primeira
definição, a modelagem de objetos por meio de
primitivas dá-se por instanciação: uma linha é
uma seqüência de pontos, uma polilinha é uma
seqüência de linhas, etc. ... Já uma
circunferência PODE ser vista como uma
polilinha fechada, onde o número de linhas
define a qualidade da curva e assim por diante.
(figura 1).
Atributo da primitiva gráfica PONTO
Figura 1. Primitivas Gráficas 2D: (A) ponto, (B) linha, (C)
polilinha, (D) retângulo, (E) dodecágono, (F)
circunferência (polilinha c/ 24 lados ou linhas).
Em CG o PONTO matemático, sem dimensão, transforma-se no PIXEL, a menor unidade gráfica
manipulável (PIXEL: de PIcture ELement).
Ao contrário do PONTO, o PIXEL tem forma, dimensão, mas estes atributos não são, em geral,
manipuláveis diretamente através de funções e dependem do hardware.
Por outro lado, em CG, tanto o PONTO quanto o PIXEL são objetos de um desenho que se inscreve
em um espaço bidimensional. No caso do ponto matemático tal espaço pertence ao R2. Já o pixel é
um elemento de uma matriz de tamanho W x H (Width-largura e Height-altura, em pixels, da matriz
do dispositivo gráfico de saída), cujas coordenadas pertencem ao N2. (R é o conjunto dos números
reais e N é o conjunto dos naturais).
Assim, podemos atribuir ao pixel apenas duas propriedades fundamentais: COR e POSIÇÃO.
Como as coordenadas do PONTO, que formam um VETOR com valores no espaço real, e as
coordenadas do PIXEL são elementos de uma MATRIZ, possuindo coordenadas inteiras e
positivas, devemos converter os valores adequadamente.
Esse cálculo é denominado de MAPEAMENTO WINDOW-TO-VIEWPORT. Podemos chamá-lo de
RASTERIZAÇÃO do ponto, já que o termo rasterização (rastering) é o processo de converter
vetores para pixels em dispositivos raster. (lembre que as coordenadas de um ponto é uma grandeza
vetorial).
O MAPEAMENTO WINDOW-TO-VIEWPORT
Sejam XR e YR as coordenadas (reais) de um ponto pertencente ao R2 e XP e YP (o P refere-se a
Pixel) as coordenadas do pixel correspondente (inteiros positivos) na matriz gráfica (tela ou
canvas).
3
As coordenadas reais (XR, YR) são, muitas vezes, referidas como COORDENADAS DO
UNIVERSO (ou do MUNDO) e estão descritas em um SISTEMA DE REFERÊNCIA DO
UNIVERSO (SRU), ou sistema de referências do mundo. São, em última análise, as coordenadas
que usamos normalmente na modelagem de objetos matemáticos.
Por outro lado, as coordenadas inteiras (XP, YP) são descritas no SISTEMA DE REFERÊNCIA
DO DISPOSITIVO gráfico de saída (SRD). Quando elas representam diretamente os valores das
LINHAS e COLUNAS no dispositivo gráfico, portanto valores inteiros que correspondem aos
índices dos elementos da matriz de pixel, serão referidas como coordenadas do dispositivo. Caso
essas coordenadas expressem os VALORES REAIS de seus respectivos pontos no SRU, serão
referidas como COORDENADAS LÓGICAS.
Uma vez que o espaço disponível para desenho no dispositivo gráfico de saída é limitado pela
matriz de pixels, devemos especificar os valores mínimos e máximos de uma JANELA DE
VISUALIZAÇÃO (viewport) na qual visualizaremos o nosso modelo matemático (desenho, função,
etc...)
Portanto, a viewport corresponde a uma área no interior da matriz de pixels do dispositivo de saída
gráfica. Ela pode corresponder a toda a matriz, como podem haver várias viewports no dispositivo,
sobrepostas ou não...
Já o plano cartesiano onde localizamos as coordenadas reais (XR, YR) é infinito. Para
representarmos qualquer modelo matemático deste espaço no interior da viewport, devemos definir
um DOMÍNIO que contém os objetos a serem representados. Esse domínio será chamado de
WINDOW por falta de um nome melhor. A window tem o mesmo papel de uma janela no sentido
comum, através da qual vemos uma cena que queremos representar. Cada elemento primitivo
descrito no interior da window será, então, MAPEADO na viewport.
Frequentemente os objetos geométricos são descritos (modelados) em um sistema próprio,
denominado SISTEMA DE REFERENCIA DO OBJETO (SRO). Veja o esquema de mapeamento
mostrado na figura 2.
SRO
SRU
window
SRD
viewport
Figura 2. Esquema SRO SRU  SRD. À esquerda, três primitivas gráficas (triângulo, quadrado, sol) modeladas no sistema
de referência do objeto (SRO), normalizado no intervalo [-1, 1]. Ao centro, uma composição com essas primitivas, devidamente
transformadas, (rotação, escala e translação) inseridas no sistema de referência do universo (SRU) com a respectiva window. À
direita um exemplo de dispositivo de saída gráfica com uma viewport exibindo a cena contida na window. Observe as distorções
e recortes da cena. O piso é formado pela mesma primitiva quadrado repintada de verde.
O mapeamento window-to-viewport ocorre diretamente entre os SRU e o SRD, mas podemos usar
as coordenadas lógicas como coordenadas intermediárias no mapeamento.
4
Outro sistema de referência utilizado na modelagem de objetos é o SISTEMA DE REFERÊNCIA
NORMALIZADO (SRN). O SRN nada mais é do que o SRO limitado no intervalo [0, 1] ou [-1, 1]
em cada uma de suas coordenadas.
Sejam, portanto, XRMIN e XRMAX os valores mínimos e máximos horizontais da janela no
espaço cartesiano (window) e XPMIN e XPMAX os valores correspondentes em pixel (viewport).
YRMIN, YRMAX, YPMIN e YPMAX serão os valores limites na vertical (c.f. figura 3). A
transformação (XR,YR)  (YP,YP) é obtida por meio de um simples cálculo de
PROPORCIONALIDADE (regra de três simples!). Para a coordenada horizontal (coordenada x) a
transformação é:
XP  XPMIN XPMAX  XPMIN

XR  XRMIN XRMAX  XRMIN
Resolvendo XR em função de XP e XP em função de XR obtemos as relações:
XP 
XP  SX  XR  XRMIN   XPMIN
XPMAX  XPMIN
 XR  XRMIN   XPMIN  
XRMAX

XRMIN
 XR  ( XP  XPMIN ) / SX  XRMIN




SX ( fatorde Escala)
onde SX é o fator de escala na dimensão horizontal
Figura 3. Rasterização de ponto
Expressões análogas são obtidas da mesma forma para a transformação da coordenada vertical (y)
Ao implementarmos essas expressões em alguma linguagem de programação devemos observar os
tipos primitivos das variáveis (XR , YR) e (XP, YP). As primeira são de tipo real, ponto flutuante, e
as outras são de tipo inteiro, o que implica em converter adequadamente os tipos.
5
MÓDULO 3.
Algoritmos de rasterização de linhas.





A equação da reta.
O algoritmo DDA (Digital Differencial Analyser).
O algoritmo de Bresenham.
Extensão para traçado de linhas em qualquer direção.
Técnicas de anti-serrilhamento (antialiasing).
RASTERIZAÇÃO DE LINHAS
Vimos como transformar as coordenadas reais de um ponto nas coordenadas de um pixel no interior
de uma janela de visualização (mapeamento window-to-viewport). Não devemos nos esquecer que
esse mapeamento converte tanto pontos do SRU em pixels do SRD como o contrário, ou seja, dado
um pixel no SRD calcula-se o ponto no SRU. Desta vez, vamos ligar dois pixels para obtermos uma
linha reta.
A motivação é simples. Em vez de mapearmos do SRU para o SRD cada ponto de uma aresta que
liga dois vértices, mapeamos apenas os vértices no interior da viewport e completamos as arestas
com um algoritmo que considere apenas os pixels do SRD.
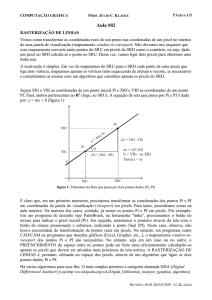
Sejam XRi e YRi as coordenadas de um ponto inicial Pi e XRf e YRf as coordenadas de um ponto
Pf, final, ambos pertencentes ao R2 (logo, ao SRU). A equação da reta que passa por Pi e Pf é dada
por: y = mx + b (figura 1)
Pf
YRf
y
Pi
YRi
x
=m
+b
Y = YRf - YRi

m = Y/ X
b = YRi - m.XRi
Tan() = m
X = XRf - XRi
b
XRi
XRf
figura 1. Elementos da Reta que passa por dois pontos dados (Pi, Pf)
É claro que, em um primeiro momento, precisamos transformar as coordenadas dos pontos Pi e Pf
em pixels, coordenadas da janela de visualização (viewport). Para tanto, procedemos como no
módulo anterior. Na maioria dos casos, contudo, já temos os pontos Pi e Pf em pixels. Por exemplo:
Em um programa de desenho tipo PaintBrush, na ferramenta "linha", pressionamos o botão do
mouse para indicar o pixel inicial (Pi). Em seguida, arrastamos o ponteiro através da tela com o
botão do mouse pressionado e soltamos, indicando o ponto final (Pf). Neste caso, observe, não
houve necessidade de transformação de pontos reais em pixels. No entanto, em programas como
6
CAD/CAM ou programas que desenham gráficos (Excel, Grapher, etc...), o mapeamento windowto-viewport dos pontos Pi e Pf é necessário. No entanto, seja em um caso ou no outro, o
PREENCHIMENTO do espaço entre os pontos para gerar uma linha reta pode ser feito mais
eficientemente calculando-se apenas os pixels que devem ser ativados MAIS PRÓXIMOS da reta
teórica. A RASTERIZAÇÃO DE LINHAS é, portanto, efetuada no espaço dos pixels, através de
um algoritmo que ligue os dois pontos dados na viewport do SRD.
Há vários algoritmos para esse fim. O mais simples pertence a categoria chamada DDA (Digital
Differencial Analizer) [veja http://en.wikipedia.org/wiki/Digital_Differential_Analyzer_(graphics_algorithm)]
Basicamente, os DDAs são ALGORITMOS INCREMENTAIS que se utilizam diretamente da
definição de reta dada por sua equação: y = mx +b. Algoritmos incrementais são aqueles em que
uma das variáveis é obtida apenas incrementando o seu valor, por exemplo X = X + 1, e a outra é
calculada por alguma regra a partir da primeira.
Vamos ligar os pixels (XPi, YPi) e (XPf, YPf)...
Primeiro calculamos os parâmetros da reta e inicializamos variáveis:




n = XPf-XPi
m = (YPf-YPi)/n
X0 = XPi
Y0 = YPi
Observe que "n" é o número de colunas de pixels entre Pi e Pf e que Y0 também pode ser entendido
como Y0 = m*X0 + b.
Em seguida incrementamos sucessivos Xs e calculamos os Ys correspondentes pela definição da
reta:


X1 = X0 + 1
Y1 = m.X1 + b = m*(X0+1) + b = m*X0 + m + b = m*X0 + b + m  Y1 = Y0 + m
Continuando (faça as contas!)...


X2 = X1 + 1  X2 = X0 + 2
Y2 = Y0 + 2*m


X3 = X0 + 3
Y3 = Y0 + 3*m

...
Por indução, obtemos uma expressão geral para o j-ésimo ponto:


Xj = X0 + j
Yj = Y0 + j*m
O último ponto será o ponto n


Xn = X0 + n
Yn = Y0 + n*m ~ YPf
Observe que Yn ~ YPf porque o resultado da expressão n*m é truncado (ou, se preferir,
arredondado), introduzindo um pequeno erro que pode ser de até um pixel.
Os pontos fracos nos algoritmos DDAs são o uso da ARITMÉTICA REAL e uma pequena
imprecisão por ERROS DE ARREDONDAMENTO.
Além dessas desvantagens, que são bastante indesejáveis, o algoritmo apresenta uma restrição
importante: ele funciona apenas para retas onde |m|  1, ou seja, retas com inclinações entre -45° e
45°. Para obtermos corretamente as demais inclinações, devemos lançar mão de SIMETRIAS.
Por exemplo, podemos dividir o plano cartesiano em oito fatias, ou OCTANTES. Para cada um
deles as retas assumem direções diferentes. O algoritmo descrito foi pensado para servir no
PRIMEIRO OCTANTE, mas funciona também no OITAVO OCTANTE. Com uma pequena
7
modificação pode-se facilmente estendê-lo para os QUARTO e QUINTO OCTANTES (pense em
como isso pode ser feito!). Os demais também podem ser obtidos a partir dessas extensões
transpondo as variáveis X  Y.
ALGORITMO DE BRESEHAM PARA SEGMENTOS DE RETAS
Outra família de Algoritmos é formada pelos ALGORITMO DE BRESENHAM e ALGORITMO
DO PONTO MÉDIO1
Esses algoritmos não usam diretamente a definição da reta, mas sim as DIFERENÇAS, ou as
distâncias (erro) entre os pixels adjacentes à reta desejada. Como nos DDAs, são algoritmos
incrementais. Entretanto, diferentemente, AMBAS AS VARIÁVEIS são incrementadas de uma
quantidade inteira. Assim, para cada X = X + 1 o valor de Y é decidido pelo algoritmo
incrementando-se ou não em função de alguns testes de diferenças. Ou seja, faz-se Y = Y ou Y = Y
+ 1 conforme o caso. Procure na Internet algum site onde o algoritmo de Bresenham é obtido para
mais informação de como é seu desenvolvimento matemático. Detalhe, Jack Bresenham trabalhava
na IBM na década de 1960 quando desenvolveu esses algoritmos para rasterização de linhas e
curvas
O algoritmo de Bresenham baseia-se no argumento de que um segmento de reta, ao ser plotado,
deve ser contínuo, ou melhor, os pixels que compõem um segmento de reta devem ser vizinhos.
Uma vez que o algoritmo também é pensado para o PRIMEIRO OCTANTE, discutiremos o caso de
0m1
Aqui, o ponto de partida é a seguinte pergunta: se 0  m  1, e dado
um ponto de um segmento de reta (x,y) o próximo pixel a ser pintado
será o (x+1, y) ou o (x+1, y+1) ? O algoritmo de Breseham responde
esta questão calculando uma variável de teste (p no algoritmo dado
abaixo) para cada pixel, e passando para o pixel seguinte, até
alcançar o último pixel do segmento de reta (c.f. figura 2).
y+2
?
y+1
s
t
y
?
x
x+1
x+2
x+3…
Figura 2: Algoritmo de Bresenham
(Coordenadas Lógicas)
Vejamos como podemos descrever o algoritmo de Bresenham...
Parâmetros de entrada: (xi, yi) e (xf, yf) (pontos inicial e final do segmento de reta)
1. Calcula-se  x  xf – xi
e
y  yf – yi.
2. Coloca-se nas variáveis de trabalho o ponto inicial:
3. Calcula-se o parâmetro de decisão:
x  xi
e
y  yi
p  2y - x
4. Plota-se o ponto (x, y).
5. Se p for negativo (isto é, se p < 0) então: x  x + 1,
6. Se p for positivo ou zero então:
x  x + 1,
p  p + 2y e passa-se para o passo 7.
yy+1
e
p  p + 2y - 2x
7. Repete-se os passos 4 a 6 até que o ponto (xf, yf) seja alcançado.
Note que o algoritmo de Bresenham (e o algoritmo do ponto médio) também só calcula linhas que
estejam entre 0 e 45°, ou seja, se 0  m  1, primeiro OCTANTE. As alterações necessárias para
estender o algoritmo para os demais octantes não parecem tão triviais quando no caso do DDA. O
emprego de SIMETRIAS é muito comum nos algoritmos de rasterização de primitivas. Os casos
especiais y=0, x=0 ou x = y) também devem ser considerados com o objetivo de otimização.
1
Há uma pequena confusão de nomenclatura nas diferentes referências. Ambos algoritmos, Bresenham e Ponto Médio,
são, frequentemente, tidos como a mesma coisa, pois geram os mesmos pixels.
8
A principal desvantagens do algoritmo de Bresenham é sua implementação, o que é completamente
irrelevante no contexto da relação programador x usuário. Um bom programador é aquele que
procura implementar bons algoritmos, ou seja, algoritmos com máxima eficiência. Já o usuário
espera um resultado limpo e preciso, que é o que o algoritmo de Bresenham oferece, ao contrário do
DDA. Como vantagens altamente desejáveis do algoritmo de Bresenham podemos citar: o uso de
aritmética inteira, o que o torna rápido na execução e mais facilmente tratável em nível de
linguagem de máquina, e preciso, ou seja, ele rigorosamente começa no pixel inicial e termina no
pixel final, possibilitando uma concatenação limpa de polilinhas, sem superposições e duplicação
de pixels.
9