COMPUTAÇÃO GRÁFICA
PÁGINA 1/5
PROF. JÚLIO C. KLAFKE
Aula #02
RASTERIZAÇÃO DE LINHAS
Vimos como transformar as coordenadas reais de um ponto nas coordenadas de um pixel no interior
de uma janela de visualização (mapeamento window-to-viewport). Não devemos nos esquecer que
esse mapeamento converte tanto pontos do SRU em pixels do SRD como o contrário, ou seja, dado
um pixel no SRD calcula-se o ponto no SRU. Desta vez, vamos ligar dois pixels para obtermos uma
linha reta.
A motivação é simples. Em vez de mapearmos do SRU para o SRD cada ponto de uma aresta que
liga dois vértices, mapeamos apenas os vértices (não esquecendo de efetuar o recorte, se necessário)
e completamos as arestas com um algoritmo que considere apenas os pixels do SRD.
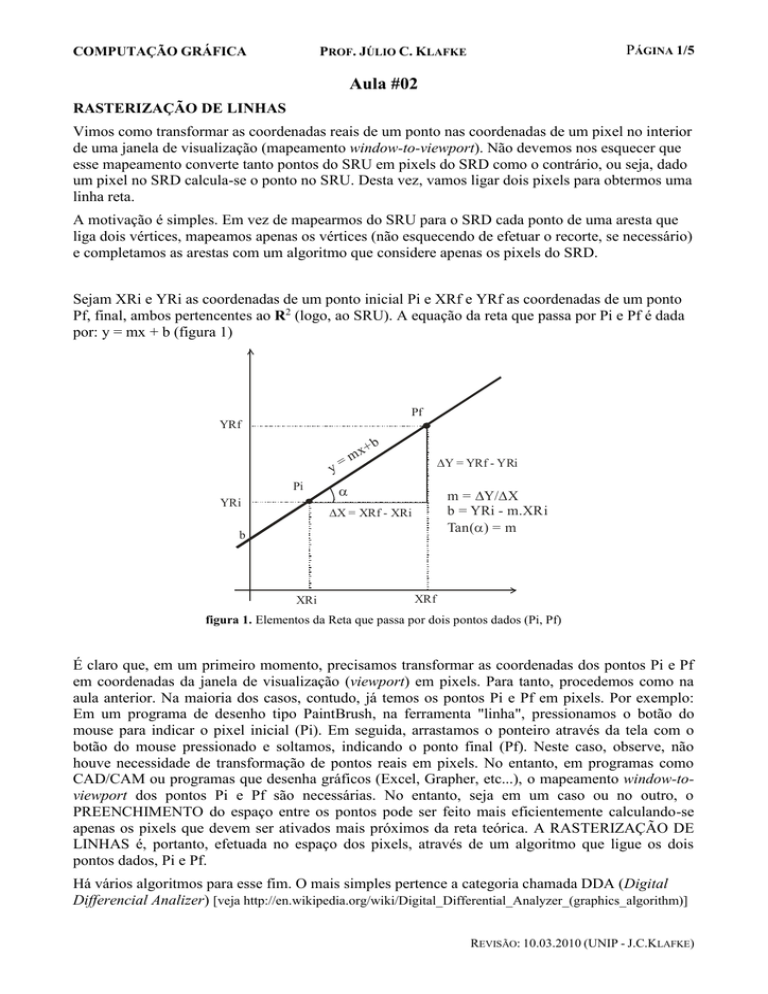
Sejam XRi e YRi as coordenadas de um ponto inicial Pi e XRf e YRf as coordenadas de um ponto
Pf, final, ambos pertencentes ao R2 (logo, ao SRU). A equação da reta que passa por Pi e Pf é dada
por: y = mx + b (figura 1)
Pf
YRf
y
Pi
YRi
x
=m
+b
Y = YRf - YRi
m = Y/ X
b = YRi - m.XRi
Tan() = m
X = XRf - XRi
b
XRi
XRf
figura 1. Elementos da Reta que passa por dois pontos dados (Pi, Pf)
É claro que, em um primeiro momento, precisamos transformar as coordenadas dos pontos Pi e Pf
em coordenadas da janela de visualização (viewport) em pixels. Para tanto, procedemos como na
aula anterior. Na maioria dos casos, contudo, já temos os pontos Pi e Pf em pixels. Por exemplo:
Em um programa de desenho tipo PaintBrush, na ferramenta "linha", pressionamos o botão do
mouse para indicar o pixel inicial (Pi). Em seguida, arrastamos o ponteiro através da tela com o
botão do mouse pressionado e soltamos, indicando o ponto final (Pf). Neste caso, observe, não
houve necessidade de transformação de pontos reais em pixels. No entanto, em programas como
CAD/CAM ou programas que desenha gráficos (Excel, Grapher, etc...), o mapeamento window-toviewport dos pontos Pi e Pf são necessárias. No entanto, seja em um caso ou no outro, o
PREENCHIMENTO do espaço entre os pontos pode ser feito mais eficientemente calculando-se
apenas os pixels que devem ser ativados mais próximos da reta teórica. A RASTERIZAÇÃO DE
LINHAS é, portanto, efetuada no espaço dos pixels, através de um algoritmo que ligue os dois
pontos dados, Pi e Pf.
Há vários algoritmos para esse fim. O mais simples pertence a categoria chamada DDA (Digital
Differencial Analizer) [veja http://en.wikipedia.org/wiki/Digital_Differential_Analyzer_(graphics_algorithm)]
REVISÃO: 10.03.2010 (UNIP - J.C.KLAFKE)
COMPUTAÇÃO GRÁFICA
PÁGINA 2/5
PROF. JÚLIO C. KLAFKE
Basicamente, os DDAs são ALGORITMOS INCREMENTAIS que se utilizam diretamente da
definição de reta dada por sua equação: y = mx +b. Algoritmos incrementais são aqueles em que
uma das variáveis é obtida apenas incrementando o seu valor, por exemplo X = X + 1, e a outra é
calculada por alguma regra a partir da primeira.
Vamos ligar os pontos (pixels) (XPi, YPi) e (XPf, YPf)...
Primeiro calculamos os parâmetros da reta e inicializamos variáveis:
n = XPf-XPi
m = (YPf-YPi)/n
X0 = XPi
Y0 = YPi
Observe que "n" é o número de colunas de pixels entre Pi e Pf e que Y0 também pode ser entendido
como Y0 = m*X0 + b.
Em seguida incrementamos sucessivos Xs e calculamos os Ys correspondentes pela definição da
reta:
X1 = X0 + 1
Y1 = m.X1 + b = m*(X0+1) + b = m*X0 + m + b = m*X0 + b + m Y1 = Y0 + m
Continuando (faça as contas!)...
X2 = X1 + 1 X2 = X0 + 2
Y2 = Y0 + 2*m
X3 = X0 + 3
Y3 = Y0 + 3*m
...
Por indução, obtemos uma expressão geral para o j-ésimo ponto:
Xj = X0 + j
Yj = Y0 + j*m
O último ponto será o ponto n
Xn = X0 + n
Yn = Y0 + n*m ~ YPf
Observe que Yn ~ YPf porque o resultado da expressão n*m é truncado (ou, se preferir,
arredondado), introduzindo um pequeno erro que pode ser de até um pixel.
Os pontos fracos nos algoritmos DDAs são o uso da ARITMÉTICA REAL e uma pequena
imprecisão por ERROS DE ARREDONDAMENTO.
Além dessas desvantagens, que são bastante indesejáveis, o algoritmo apresenta uma restrição
importante: ele funciona apenas para retas onde |m| 1, ou seja, retas com inclinações entre -45° e
45°. Para obtermos corretamente as demais inclinações, devemos lançar mão de SIMETRIAS.
Por exemplo, podemos dividir o plano cartesiano em oito fatias, ou OCTANTES. Para cada um
deles as retas assumem direções diferentes. O algoritmo descrito foi pensado para servir no
PRIMEIRO OCTANTE, mas funciona também no OITAVO OCTANTE. Com uma pequena
modificação pode-se facilmente estendê-lo para os QUARTO e QUINTO OCTANTES (pense em
como isso pode ser feito!). Os demais também podem ser obtidos a partir dessas extensões
transpondo as variáveis X Y.
REVISÃO: 10.03.2010 (UNIP - J.C.KLAFKE)
COMPUTAÇÃO GRÁFICA
PÁGINA 3/5
PROF. JÚLIO C. KLAFKE
ALGORITMO DE BRESEHAM PARA SEGMENTOS DE RETAS
Outra família de Algoritmos é formada pelos ALGORITMO DE BRESENHAM e ALGORITMO
DO PONTO MÉDIO1
Esses algoritmos não usam diretamente a definição da reta, mas sim as DIFERENÇAS, ou as
distâncias (erro) entre os pixels adjacentes à reta desejada. Como nos DDAs, são algoritmos
incrementais. Entretanto, diferentemente, ambas as variáveis são incrementadas de uma quantidade
inteira. Assim, para cada X = X + 1 o valor de Y é decidido pelo algoritmo incrementando-se ou
não em função de alguns testes de diferenças. Ou seja, faz-se Y = Y ou Y = Y + 1 conforme o caso.
Procure na Internet algum site onde o algoritmo de Bresenham é obtido para mais informação de
como é seu desenvolvimento matemático. Detalhe, Jack Bresenham trabalhava na IBM na década
de 1960 quando desenvolveu esses algoritmos para rasterização de linhas e curvas
O algoritmo de Bresenham baseia-se no argumento de que um segmento de reta, ao ser plotado,
deve ser contínuo, ou melhor, os pixels que compõem um segmento de reta devem ser vizinhos.
Uma vez que o algoritmo também é pensado para o PRIMEIRO OCTANTE, discutiremos o caso de
0m1
Aqui, o ponto de partida é a seguinte pergunta: se 0 m 1, e dado
um ponto de um segmento de reta (x,y) o próximo pixel a ser pintado
será o (x+1, y) ou o (x+1, y+1) ? O algoritmo de Breseham responde
esta questão calculando uma variável de teste (p no algoritmo dado
abaixo) para cada pixel, e passando para o pixel seguinte, até
alcançar o último pixel do segmento de reta (c.f. figura 2).
y+2
?
y+1
s
t
y
?
x
x+1
x+2
x+3…
Figura 2: Algoritmo de Bresenham
(Coordenadas Lógicas)
Vejamos como podemos descrever o algoritmo de Bresenham...
Parâmetros de entrada: (x1,y1) e (x2,y2) (pontos inicial e final do segmento de reta)
1. Calcula-se
x x2 - x1
e
y y2 - y1.
2. Coloca-se nas variáveis de trabalho o ponto inicial:
x x1
e
y y1
3. Calcula-se o parâmetro de decisão:
p 2y - x
4. Plota-se o ponto (x,y).
5. Se p for negativo (isto é, se p < 0) então:
xx+1
,
p p + 2y
e passa-se para o passo 7.
6. Se p for positivo ou zero então:
xx+1
,
yy+1
e
p p + 2y - 2x
7. Repete-se os passos 4 a 6 até que o ponto (x2,y2) seja alcançado.
1
Há uma pequena confusão de nomenclatura nas diferentes referências. Ambos algoritmos, Bresenham e Ponto Médio,
são, frequentemente, tidos como a mesma coisa, pois geram os mesmos pixels.
REVISÃO: 10.03.2010 (UNIP - J.C.KLAFKE)
COMPUTAÇÃO GRÁFICA
PÁGINA 4/5
PROF. JÚLIO C. KLAFKE
Note que também o algoritmo de Bresenham (e o algoritmo do ponto médio) só calcula linhas que
estejam entre 0 - 45°, ou seja, se 0 m 1, primeiro OCTANTE. As alterações necessárias para
estender o algoritmo para os demais octantes não parecem tão triviais quando no caso do DDA. O
emprego de SIMETRIAS é muito comum nos algoritmos de rasterização de primitivas. Os casos
especiais y=0, x=0 ou x = y) também devem ser considerados com o objetivo de otimização.
A principal desvantagens do algoritmo de Bresenham é sua implementação, o que é completamente
irrelevante no contexto da relação programador x usuário. Um bom programador é aquele que
procura implementar bons algoritmos, ou seja, algoritmos com máxima eficiência. Já o usuário
espera um resultado limpo e preciso, que é o que o algoritmo de Bresenham oferece, ao contrário do
DDA. Como vantagens altamente desejáveis do algoritmo de Bresenham podemos citar: o uso de
aritmética inteira, o que o torna rápido na execução e mais facilmente tratável em nível de
linguagem de máquina, e preciso, ou seja, ele rigorosamente começa no pixel inicial e termina no
pixel final, possibilitando uma concatenação limpa de polilinhas, sem superposições e duplicação
de pixels.
EXERCÍCIOS
1.
Pesquise o termo RASTERIZAÇÃO e escreva uma definição para o mesmo usando suas
próprias palavras.
2.
Escreva a equação da reta que passa pelos pontos A = (0.5, 1.5) e B = (2.0, 3.5). Quais os
valores dos coeficientes linear e angular da mesma?
3.
Ao traçarmos a ARESTA (segmento de reta)
entre dois VÉRTICES (pontos) A e B, apenas o
segmento A'B' que encontra-se no interior da
window deve ser representado (o clipping na
figura 3, ao lado). Pense no caso mais simples
onde só o vértice A encontra-se no exterior da
window (ou seja, o segmento de reta
representável é o A'B). Ache as coordenadas do
ponto A' para o caso em que
A = (0.5, 1.5), B = (2.5, 2.5) e uma window
limitada por (1.0, 1.0) - (3.0, 3.0).
SRU
B
YRMAX
B'
A
A'
window
YRMIN
XRMIN
XRMAX
3.. Faça uma pesquisa sobre RECORTE (clipping) na computação gráfica e escreva uma
definição sumária usando suas próprias palavras. Liste os principais algoritmos, destacando
suas vantagens e desvantagens. Sugestão inicial: <http://en.wikipedia.org/wiki/Line_clipping>
4.
Desenhe uma grade quadriculada de 10 x 10 quadrados. Esse será o seu gabarito para a
matriz de pixels de um dispositivo matricial gráfico hipotético. Considere coordenadas
lógicas do dispositivo, com o pixel de coordenadas (0, 0) no canto inferior esquerdo e o
pixel de coordenadas (9, 9) no canto superior direito.
a) Assinale os pixels (vértices) de coordenadas A = (0, 5), B = (7, 8) e C = (4, 0).
b) Ligue os vértices ABC de (a) com um linhas retas simples partindo do centro
geométrico de cada quadrado (pixel). Use uma régua.
c) Intuitivamente, preencha os pixels (quadrados) que você acha que melhor representam
as linhas assinaladas em (b).
5.
Escreva (e não copie de uma outra fonte qualquer) um pseudocódigo para o algoritmo DDA
descrito no texto considerando as alterações necessárias para que ele trace linhas em todas as
direções, inclusive linhas verticais e teste-o, comparando seus resultados com os pixels
assinalados por você na questão 4(c)
REVISÃO: 10.03.2010 (UNIP - J.C.KLAFKE)
COMPUTAÇÃO GRÁFICA
PROF. JÚLIO C. KLAFKE
PÁGINA 5/5
6.
Teste o algoritmo de Bresenham para rasterização de linhas, como descrito no texto,
comparando seus resultados com os pixels assinalados por você na questão 4(c) e 5
7.
Um efeito indesejável que resulta do processo de discretização dos pixels no traçado de
linhas é o efeito de SERRILHAMENTO (o termo em inglês é aliasing, embora aliasing não
se traduza como serrilhamento). Para atenuá-lo, ou eliminá-lo, devemos lançar mão de
técnicas de ANTI-SERRILHAMENTO (anti-aliasing, ou AA). A técnica mais simples é a da
super amostragem (supersampling). Pesquise sobre essa técnica (que possui várias formas
de implementação) e tente explicá-la, resumidademente, usando suas próprias palavras.
8.
Uma forma muito simples de se tentar minimizar o efeito de serrilhamento pode ser obtida
acendendo ambos os pixel, y e y + 1, com tons intermediários. No algoritmo DDA, por
exemplo, podemos optar por arredondar o incremento j*m. Neste caso, o valor truncado
poderia ser pintado com uma tonalidade mais clara. Para garantir que a cor da reta seja
preservada, devemos primeiro pintar o pixel mais claro e depois pintamos o pixel correto
com o tom desejado. Implemente um algoritmo para testar essa idéia e observe o resultado
(ou use-a com o exemplo da questão 5). Como essa mesma idéia poderia ser implementada
com o algoritmo de Bresenham?
REVISÃO: 10.03.2010 (UNIP - J.C.KLAFKE)












