EXERCÍCOS DE FÍSICA - Professor Fabio Teixeira

Colégio: ________________________________________________________________________
Professor: ____________________ Turma: ___________________ Turno: __________________
Aluno: _________________________________________________ n____ Data: ___/___/______
DINÂMICA DO MOVIMENTO CIRCULAR
1. Um circuito de Fórmula Mundial circular, com 320 m
de raio, tem como velocidade de segurança 40 m/s.
Calcule a tangente do ângulo de inclinação da pista.
Observação: velocidade de segurança é a velocidade com
a qual o carro pode trafegar sem que nenhuma força de
atrito lateral seja exercida em suas rodas.
2. (Fuvest 2004) Um brinquedo consiste em duas
pequenas bolas A e B, de mesma massa M, e um fio
flexível: a bola B está presa na extremidade do fio e a bola
A possui um orifício pelo qual o fio passa livremente. Para
o jogo, um operador (com treino!) deve segurar o fio e
girá-lo, de tal forma que as bolas descrevam trajetórias
circulares, com o mesmo período T e raios diferentes.
Nessa situação, como indicado na figura 1, as bolas
permanecem em lados opostos em relação ao eixo vertical
fixo que passa pelo ponto O. A figura 2 representa o plano
que contém as bolas e que gira em torno do eixo vertical,
indicando os raios e os ângulos que o fio faz com a
horizontal.
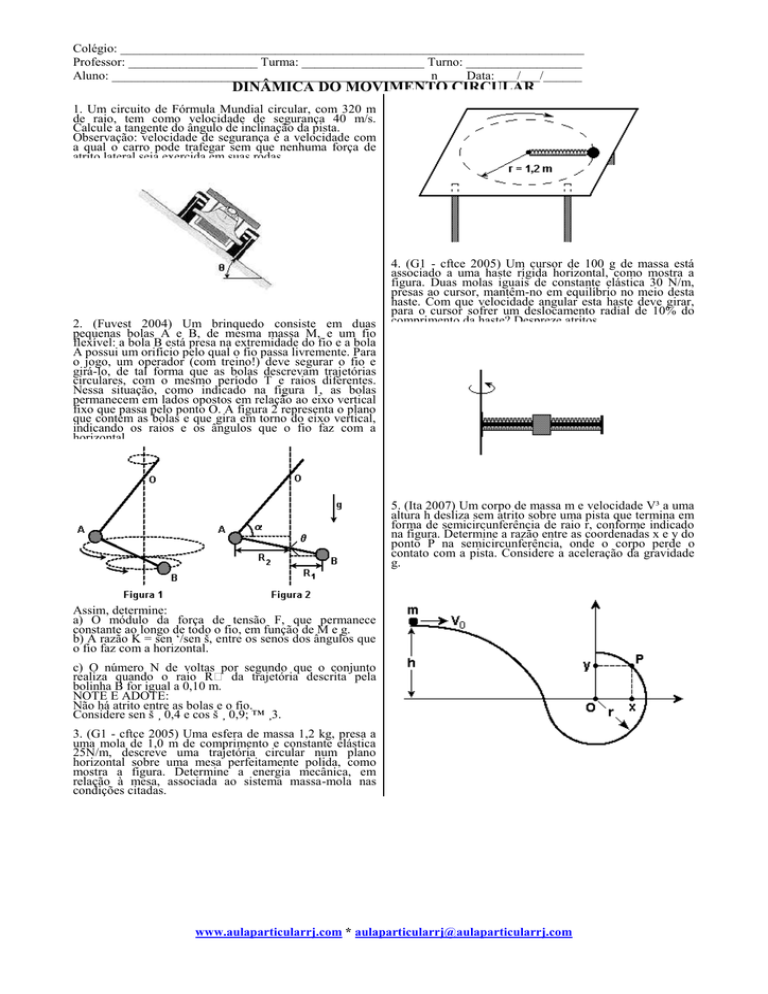
4. (G1 - cftce 2005) Um cursor de 100 g de massa está
associado a uma haste rígida horizontal, como mostra a
figura. Duas molas iguais de constante elástica 30 N/m,
presas ao cursor, mantêm-no em equilíbrio no meio desta
haste. Com que velocidade angular esta haste deve girar,
para o cursor sofrer um deslocamento radial de 10% do
comprimento da haste? Despreze atritos.
5. (Ita 2007) Um corpo de massa m e velocidade V³ a uma
altura h desliza sem atrito sobre uma pista que termina em
forma de semicircunferência de raio r, conforme indicado
na figura. Determine a razão entre as coordenadas x e y do
ponto P na semicircunferência, onde o corpo perde o
contato com a pista. Considere a aceleração da gravidade
g.
Assim, determine:
a) O módulo da força de tensão F, que permanece
constante ao longo de todo o fio, em função de M e g.
b) A razão K = sen ‘/sen š, entre os senos dos ângulos que
o fio faz com a horizontal.
c) O número N de voltas por segundo que o conjunto
realiza quando o raio R• da trajetória descrita pela
bolinha B for igual a 0,10 m.
NOTE E ADOTE:
Não há atrito entre as bolas e o fio.
Considere sen š ¸ 0,4 e cos š ¸ 0,9; ™ ¸3.
3. (G1 - cftce 2005) Uma esfera de massa 1,2 kg, presa a
uma mola de 1,0 m de comprimento e constante elástica
25N/m, descreve uma trajetória circular num plano
horizontal sobre uma mesa perfeitamente polida, como
mostra a figura. Determine a energia mecânica, em
relação à mesa, associada ao sistema massa-mola nas
condições citadas.
www.aulaparticularrj.com * [email protected]
Colégio: ________________________________________________________________________
Professor: ____________________ Turma: ___________________ Turno: __________________
Aluno: _________________________________________________ n____ Data: ___/___/______
6. (Ufg 2006) O chapéu mexicano, representado na figura, 8. (Ufrj 2006) Uma caixa é pendurada no teto de um
gira com velocidade angular constante. Cada assento é ônibus por meio de fios ideais presos a um dinamômetro
preso por quatro correntes, que formam com a vertical um de massa desprezível. A figura mostra esses objetos em
ângulo de 30°. As correntes estão presas à borda do equilíbrio em relação ao ônibus, enquanto ele está
círculo superior, cujo diâmetro é de 6,24 m, enquanto o percorrendo um trecho circular de uma estrada horizontal,
comprimento das correntes é de 6 m. A massa de cada com velocidade de 72 km/h. Nessa situação, o
criança é de 34 kg, sendo desprezíveis as massas dos dinamômetro mostra que a tensão no fio é 65 N.
assentos e das correntes. Dados: g = 10 m/s£, Ë3 = 1,7
Sabendo que a massa da caixa é 6,0 kg, calcule o raio da
curva da estrada.
Calcule:
a) a velocidade delas ao longo da trajetória circular;
b) a tensão em cada corrente.
7. (Ufrj 2005) Um trilho em forma de arco circular,
contido em um plano vertical, está fixado num ponto A de
um plano horizontal. O centro do arco está em um ponto
O desse mesmo plano. O arco é de 90° e tem raio R, como
ilustra a figura 1.
Um pequeno objeto é lançado para cima, verticalmente, a
partir da base A do trilho e desliza apoiado a ele, sem
atrito, até o ponto B, onde escapa horizontalmente, caindo
no ponto P do plano horizontal onde está fixado o trilho.
A distância do ponto P ao ponto A é igual a 3R como
ilustra a figura 2.
Calcule o módulo da velocidade inicial ¬³ com que o
bloco foi lançado, em função do raio R e da aceleração g
da gravidade.
9. (Ufrrj 2005) Foi que ele viu Juliana na roda com João
Uma rosa e um sorvete na mão
Juliana seu sonho, uma ilusão
Juliana e o amigo João
GIL, Gilberto. "Domingo no Parque".
A roda citada no texto é conhecida como RODAGIGANTE, um brinquedo de parques de diversões no qual
atuam algumas forças, como a força centrípeta.
Considere:
- o movimento uniforme;
- o atrito desprezível;
- aceleração da gravidade local de 10 m/s£;
- massa da Juliana 50 kg;
- raio da roda-gigante 2 metros;
- velocidade escalar constante, com que a roda está
girando, 36 km/h.
Calcule a intensidade da reação normal vertical que a
cadeira exerce sobre Juliana quando a mesma se encontrar
na posição indicado pelo ponto J.
10. (Unesp 2003) Um pequeno bloco de massa m é
colocado sobre um disco giratório, plano e horizontal,
inicialmente em repouso, a uma distância R do eixo do
disco. O disco é então posto a girar com pequena
aceleração angular, até que sua velocidade angular atinja
um certo valor Ÿ. A partir deste valor de velocidade
angular, o bloco começa a deslizar sobre o disco.
Representando por g a aceleração da gravidade, e
considerando o instante em que o bloco está prestes a
deslizar sobre o disco,
a) determine, em função desses dados, o módulo da força
centrípeta F(c) que atua sobre o bloco.
b) calcule, em função desses dados, o coeficiente de atrito
estático ˜(e) entre o bloco e o disco.
11. (Unifesp 2004) Uma estação espacial, construída em
forma cilíndrica, foi projetada para contornar a ausência
de gravidade no espaço. A figura mostra, de maneira
simplificada, a secção reta dessa estação, que possui dois
andares.
www.aulaparticularrj.com * [email protected]
Colégio: ________________________________________________________________________
Professor: ____________________ Turma: ___________________ Turno: __________________
Aluno: _________________________________________________ n____ Data: ___/___/______
13. (Unesp 2005) Uma espaçonave de massa m gira em
torno da Terra com velocidade constante, em uma órbita
circular de raio R. A força centrípeta sobre a nave é 1,5
GmM/R£, onde G é a constante de gravitação universal e
M a massa da Terra.
a) Desenhe a trajetória dessa nave. Em um ponto de sua
trajetória, desenhe e identifique os vetores velocidade « e
aceleração centrípeta @ da nave.
b) Determine, em função de M, G e R, os módulos da
aceleração centrípeta e da velocidade da nave.
14. (Ufc 2007) Uma partícula com carga positiva +q é
fixada em um ponto, atraindo uma outra partícula com
carga negativa -q e massa m, que se move em uma
trajetória circular de raio R, em torno da carga positiva,
com velocidade de módulo constante (veja a figura a
seguir). Considere que não há qualquer forma de
dissipação de energia, de modo que a conservação da
energia mecânica é observada no sistema de cargas.
Despreze qualquer efeito da gravidade. A constante
eletrostática é igual a k.
Para simular a gravidade, a estação deve girar em torno do
seu eixo com uma certa velocidade angular. Se o raio
externo da estação é R,
a) deduza a velocidade angular Ÿ com que a estação deve
girar para que um astronauta, em repouso no primeiro
andar e a uma distância R do eixo da estação, fique sujeito
a uma aceleração igual a g.
b) Suponha que o astronauta vá para o segundo andar, a
uma distância h do piso do andar anterior. Calcule o peso
do astronauta nessa posição e compare com o seu peso
quando estava no primeiro andar. O peso aumenta,
diminui ou permanece inalterado ?
12. (Unifesp 2004) É comum vermos, durante uma partida
de voleibol, a bola tomar repentinamente trajetórias
inesperadas logo depois que o jogador efetua um saque. A
bola pode cair antes do esperado, assim como pode ter sua
trajetória prolongada, um efeito inesperado para a baixa
velocidade com que a bola se locomove. Quando uma
bola se desloca no ar com uma velocidade v e girando
com velocidade angular Ÿ em torno de um eixo que passa
pelo seu centro, ela fica sujeita a uma força F(Magnus) =
k.v. Ÿ. Essa força é perpendicular à trajetória e ao eixo de
rotação da bola, e o seu sentido depende do sentido da
rotação da bola, como ilustrado na figura. O parâmetro k é
uma constante que depende das características da bola e
da densidade do ar.
Esse fenômeno é conhecido como efeito Magnus.
Represente a aceleração da gravidade por g e despreze a
força de resistência do ar ao movimento de translação da
bola.
a) Considere o caso em que o saque é efetuado na direção
horizontal e de uma altura maior que a altura do jogador.
A bola de massa M segue por uma trajetória retilínea e
horizontal com uma velocidade constante v, atravessando
toda a extensão da quadra. Qual deve ser o sentido e a
velocidade angular de rotação Ÿ a ser imprimida à bola no
momento do saque?
b) Considere o caso em que o saque é efetuado na direção
horizontal, de uma altura h, com a mesma velocidade
inicial v, mas sem imprimir rotação na bola. Calcule o
alcance horizontal D da bola.
a) Determine o módulo da velocidade v com que a carga
negativa se move em torno da carga positiva.
b) Determine o período do movimento circular da carga
negativa em torno da carga positiva.
c) Determine a energia total do sistema.
d) Considere que o produto da massa da partícula com
carga negativa pela sua velocidade e pelo raio da trajetória
circular é igual ao produto de um número inteiro por uma
constante; ou seja, mv R = nh, onde n é o número inteiro
(n = 1, 2, 3, ...) e h, a constante. Determine a energia total
do sistema em termos de n, h, q e k.
e) Determine a freqüência do movimento da carga
negativa em torno da carga positiva em termos de n, h, q e
k.
TEXTO PARA AS PRÓXIMAS 2 QUESTÕES.
(Fgv 2007) Vendedores aproveitam-se da morosidade do
trânsito para vender amendoins, mantidos sempre
aquecidos em uma bandeja perfurada encaixada no topo
de um balde de alumínio; dentro do balde, uma lata de
leite em pó, vazada por cortes laterais, contém carvão em
brasa (figura 1). Quando o carvão está por se acabar, nova
quantidade é reposta. A lata de leite é enganchada a uma
haste de metal (figura 2) e o conjunto é girado
vigorosamente sob um plano vertical por alguns segundos
(figura 3), reavivando a chama.
Dados:
™ = 3,1
g = 10 m/s£
15. No momento em que o braseiro atinge o ponto mais
baixo de sua trajetória, considerando que ele descreve um
movimento no sentido anti-horário e que a trajetória é
percorrida com velocidade constante, dos vetores
indicados, aquele que mais se aproxima da direção e
sentido da força resultante sobre a lata é
www.aulaparticularrj.com * [email protected]
Colégio: ________________________________________________________________________
Professor: ____________________ Turma: ___________________ Turno: __________________
Aluno: _________________________________________________ n____ Data: ___/___/______
16. Mantendo o movimento circular de raio 80 cm, a
menor velocidade que a lata deve possuir no ponto mais
alto de sua trajetória para que o carvão não caia da lata é,
em m/s,
a) Ë2
b) 2
c) 2Ë2
d) 4
e) 4Ë2
17. Observe o fenômeno indicado na tirinha a seguir.
19. (Puc-rio 2006) Um carro de massa m = 1000 kg
realiza uma curva de raio R = 20 m com uma velocidade
angular w = 10 rad/s. A força centrípeta atuando no carro
em newtons vale:
a) 2,0 10§.
b) 3,0 10§.
c) 4,0 10§ .
d) 2,0 10¦.
e) 4,0 10¦.
20. (Pucsp 2006) Um automóvel percorre uma curva
circular e horizontal de raio 50 m a 54 km/h. Adote g = 10
m/s£. O mínimo coeficiente de atrito estático entre o
asfalto e os pneus que permite a esse automóvel fazer a
curva sem derrapar é
a) 0,25
b) 0,27
c) 0,45
d) 0,50
e) 0,54
21. (Pucsp 2006) Durante uma apresentação da
Esquadrilha da Fumaça, um dos aviões descreve a
trajetória circular da figura, mantendo o módulo de sua
velocidade linear sempre constante.
A força que atua sobre o peso e produz o deslocamento
vertical da garrafa é a força
a) de inércia.
b) gravitacional.
c) de empuxo.
d) centrípeta.
e) elástica.
18. (G1 - cftce 2005) Vários blocos estão na periferia de
um disco de 15 cm de raio, que gira com velocidade
crescente. Se as massas dos blocos e seus coeficientes de
atrito com o disco são os do quadro a seguir, o que se
deslocará primeiro está indicado na letra:
Sobre o descrito são feitas as seguintes afirmações:
I - A força com a qual o piloto comprime o assento do
avião varia enquanto ele percorre a trajetória descrita.
II - O trabalho realizado pela força centrípeta que age
sobre o avião é nulo em qualquer ponto da trajetória
descrita.
III - Entre os pontos A e B da trajetória descrita pelo avião
não há impulso devido à ação da força centrípeta.
Somente está correto o que se lê em
a) I
b) II
c) III
d) II e III
22. (Pucsp 2007)
www.aulaparticularrj.com * [email protected]
e) I e II
Colégio: ________________________________________________________________________
Professor: ____________________ Turma: ___________________ Turno: __________________
Aluno: _________________________________________________ n____ Data: ___/___/______
25. (Ufpel 2006) Considere um satélite artificial que está
em órbita circular ao redor da Terra. Nessa condição, é
correto afirmar que
a) seu vetor velocidade, vetor aceleração centrípeta e seu
período são constantes.
b) seu vetor velocidade varia, seu vetor aceleração
centrípeta e seu período são constantes.
c) seu vetor velocidade e seu vetor aceleração centrípeta
variam e seu período é constante.
d) seu vetor velocidade e seu período são constantes e seu
vetor aceleração centrípeta varia.
e) seu vetor velocidade, seu vetor aceleração centrípeta e
seu período variam.
A figura representa em plano vertical um trecho dos
trilhos de uma montanha russa na qual um carrinho está
prestes a realizar uma curva. Despreze atritos, considere a
massa total dos ocupantes e do carrinho igual a 500 kg e a
máxima velocidade com que o carrinho consegue realizar
a curva sem perder contato com os trilhos igual a 36 km/h.
O raio da curva, considerada circular, é, em metros, igual
a
a) 3,6 b) 18 c) 1,0 d) 6,0 e) 10
23. (Uerj 2006) A técnica de centrifugação é usada para
separar os componentes de algumas misturas. Pode ser
utilizada, por exemplo, na preparação de frações celulares,
após o adequado rompimento das membranas das células
a serem centrifugadas.
Em um tubo apropriado, uma camada de homogeneizado
de células eucariotas rompidas foi cuidadosamente
depositada sobre uma solução isotônica de NaCØ. Esse
tubo foi colocado em um rotor de centrífuga, equilibrado
por um outro tubo.
O esquema a seguir mostra o rotor em repouso e em
rotação.
Considere as seguintes massas médias para algumas
organelas de uma célula eucariota:
- mitocôndria: 2 ×10-© g;
- lisossoma: 4 × 10-¢¡ g;
- núcleo: 4 × 10-§ g.
Durante a centrifugação do homogeneizado, em um
determinado instante, uma força centrípeta de 5 × 10-¥ N
atua sobre um dos núcleos, que se desloca com velocidade
de módulo constante de 150 m/s.
Nesse instante, a distância desse núcleo ao centro do rotor
da centrífuga equivale, em metros, a:
a) 0,12
b) 0,18
c) 0,36
d) 0,60
24. (Ufms 2006) Um satélite artificial está em órbita em
torno da Terra, de forma que mantém sempre a mesma
posição relativa a um ponto na superfície da Terra.
Qual(is) da(s) afirmação(ões) a seguir é (são) correta(s)?
(01) A velocidade angular do satélite é igual à velocidade
angular de rotação da Terra.
(02) A velocidade tangencial do satélite é igual à
velocidade tangencial de um ponto na superfície da Terra.
(04) A força centrípeta que atua sob o satélite é a força
gravitacional e tem o mesmo valor da força centrípeta de
um corpo na superfície da Terra.
(08) A velocidade tangencial do satélite depende da altura
de órbita em relação à Terra.
(16) A aceleração gravitacional do satélite é nula porque
ele está em órbita.
26. (Ufrs 2005) A figura a seguir representa um pêndulo
cônico ideal que consiste em uma pequena esfera suspensa
a um ponto fixo por meio de um cordão de massa
desprezível.
Para um observador inercial, o período de rotação da
esfera, em sua órbita circular, é constante. Para o mesmo
observador, a resultante das forças exercidas sobre a
esfera aponta
a) verticalmente para cima.
b) verticalmente para baixo.
c) tangencialmente no sentido do movimento.
d) para o ponto fixo.
e) para o centro da órbita.
27. (Unesp 2003) No modelo clássico do átomo de
hidrogênio, do físico dinamarquês Niels Bohr, um elétron
gira em torno de um próton com uma velocidade constante
de 2 × 10§ m/s e em uma órbita circular de raio igual a 5 ×
10-¢¢ m. Se o elétron
possui massa 9 × 10-¤¢ kg, a força centrípeta sobre ele é
de
a) 7,2 × 10-¢¥ N. b) 3,6 × 10-¢¥ N.
c) 8,0 × 10-¢¡ N. d) 7,2 × 10-© N.
e) 3,6 × 10-© N.
28. (Unifesp 2003) Antes de Newton expor sua teoria
sobre a força da gravidade, defensores da teoria de que a
Terra se encontrava imóvel no centro do Universo
alegavam que, se a Terra possuísse movimento de rotação,
sua velocidade deveria ser muito alta e, nesse caso, os
objetos sobre ela deveriam ser arremessados para fora de
sua superfície, a menos que uma força muito grande os
mantivesse ligados à Terra. Considerando o raio da Terra
de 7 × 10§ m, o seu período
de rotação de 9 × 10¥ s e ™£ = 10, a força mínima capaz
de manter um corpo de massa 90kg em repouso sobre a
superfície da Terra, num ponto sobre a linha do Equador,
vale, aproximadamente,
a) 3 N.
b) 10 N. c) 120 N.
d) 450 N.
e) 900 N.
www.aulaparticularrj.com * [email protected]
Colégio: ________________________________________________________________________
Professor: ____________________ Turma: ___________________ Turno: __________________
Aluno: _________________________________________________ n____ Data: ___/___/______
29. (Unifesp 2007) A trajetória de uma partícula,
representada na figura, é um arco de circunferência de raio
r = 2,0 m, percorrido com velocidade de módulo
constante, v = 3,0 m/s.
O módulo da aceleração vetorial dessa partícula nesse
trecho, em m/s£, é
a) zero.
b) 1,5.
c) 3,0.
d) 4,5.
e) impossível de ser calculado.
30. (Ueg 2006) A figura a seguir mostra uma partícula de
massa m que é mantida inicialmente em repouso na
posição A, por meio de dois fios leves AC e AD. O fio
horizontal AC é cortado e a bola começa a oscilar como
um pêndulo de comprimento L. O ponto B é o ponto mais
afastado do lado direito da trajetória das oscilações.
Desprezando todos os tipos de atrito, julgue a validade das
afirmações a seguir.
I. A razão entre a tensão do fio na posição B e a tensão do
fio na posição A, antes de o fio horizontal ser cortado, é
sec£š.
II. A velocidade da esfera ao passar pelo ponto mais baixo
da trajetória vale Ë[2Lg(1 - cosš)].
III. A aceleração da partícula no ponto B é máxima.
Assinale a alternativa CORRETA:
a) Apenas as afirmações I e II são verdadeiras.
b) Apenas as afirmações I e III são verdadeiras.
c) Apenas as afirmações II e III são verdadeiras.
d) Todas as afirmações são verdadeiras.
www.aulaparticularrj.com * [email protected]
Colégio: ________________________________________________________________________
Professor: ____________________ Turma: ___________________ Turno: __________________
Aluno: _________________________________________________ n____ Data: ___/___/______
GABARITO
1. Na horizontal N.senš = m.v£/R
Na vertical N.cosš = mg
Dividindo a primeira expressão pela segunda:
tgš = v£/(Rg) = 1600/3200 = 0,5
2. a) 2,5.Mg
b) K = 2
c) 2,5 Hz
3. Uma esfera de massa 1,2 kg, presa a uma mola de 1,0 m
de comprimento e constante elástica 25N/m, descreve uma
trajetória circular num plano horizontal sobre uma mesa
perfeitamente polida, como mostra a figura. Determine a
energia mecânica, em relação à mesa, associada ao
sistema massa-mola nas condições citadas.
E(mecânica) = E(cinética) + E(elástica)
E = m.v£/2 + k.x£/2
E = Rkx/2 + k.x£/2
E = 1,2.25.0,2/2 + 25.(0,2)£/2
E = 3 + 0,5 = 3.5 J
4. 30.0,1,H + 30,01,H = 0,1.Ÿ£.0,6.H
30 + 30 = ٣.0,6 60 = ٣.0,6
60/0,6 = ٣
Ÿ£ = 100
Ÿ = 10 rad/s
5. Aplicando o teorema de Pitágoras no triângulo OxP
temos: x£ + y£ = r£; de onde vem (x/y)£ + 1 = (r/y)£; que
vamos chamar de equação 1.
No ponto P o corpo está realizando um movimento
circular onde a força de reação da pista sobre a partícula é
nula e desta forma a componente radial da força peso será
a resultante centrípeta, ou seja, P.sen ‘ = m.v£/r, onde sen
‘ = y/r e P = mg. Desta forma mgy/r = m.v£/r então r/y =
rg/v£, que vamos chamar de equação 2.
Da conservação da energia mecânica entre o ponto inicial
e o ponto P:
m.v³£/2 + m.g.h = m.v£/2 + m.g.y
v³£ + 2.g.h = v£ + 2.g.y ë v£/r = v³£/r + 2gh/r - 2gy/r.
Substituindo esta última expressão na equação 2, temos:
r/y = 3gr/(v³£ + 2gh). Substituindo esta expressão na
equação 1:
(x/y)£ + 1 = [3gr/(v³£ + 2gh)]£
(x/y)£ + 1 = 9g£r£/(v³£ + 2gh)£
(x/y)£ = [9g£r£/(v³£ + 2gh)£] - 1
(x/y) = {[9g£r£/(v³£ + 2gh)£] - 1}
6. a) 6 m/s
b) 100 N
7. Combinando as equações, V³£ = 2gR+2gR = 4gR ou V³
= 2ËgR.
8. Aplicando o princípio fundamental da dinâmica,
F(resultante) = massa.aceleração, considerando que o
movimento da caixa é circular, tem-se:
Tcosš = mg e Tsenš = (mv£)/R, onde T é a tensão no fio, š
é o ângulo que o fio faz com a vertical, v é a velocidade da
caixa (igual à do ônibus) e R é o raio da trajetória.
Da primeira equação, obtem-se:
cosš = (mg)/T = (6 × 10)/65 = 12/13, de onde senš = Ë[1 (12/13)£] = 5/13.
A velocidade vetorial « é tangente à trajetória e tem o
sentido do movimento.
A aceleração centrípeta é dirigida para o centro da
trajetória e tem direção radial.
b) V = (Ë1,5GM)/R
14. a) v = Ë[(kq£)/(mR)]
b) T = 2™ Ë[(mR¤)/(kq£)]
c) E = -1/2 [(kq£)/R]
d) E = -1/2 . [(mk£q¥)/h£] . 1/n£
e) f = 1/2™ . [(mk£q¥)/n¤h¤]
15. [A]
16. [C]
17. [D]
18. [D]
19. [A]
20. [C]
21. [E]
22. [E]
23. [B]
24. 09 ==> AS CORRETAS SÃO 08 E 01.
25. [C]
26. [E]
27. [D]
28. [A]
29. [D]
30. [D]
Usando, então, a segunda equação, chegamos a R =
(mv)£/(Tsenš) = (6×20£×13)/(65×5) = 96m.
9. 3000 N.
10. a) Fc = m٣R
b) ˜e = Ÿ£R/g
11. a) Ÿ=Ë(g/R)
b) m.g.((R-h)/R)
12. a) o sentido anti-horário (vide figura no problema) e o
módulo Mg/(kv)
b) v.Ë(2h/g)
13. a)
www.aulaparticularrj.com * [email protected]