pptx

PESQUISA OPERACIONAL II
Professor: D. Sc. Edwin B. Mitacc Meza
[email protected]
www.engenharia-puro.com.br/edwin
Processos Estocásticos
Introdução
 Qualquer sistema real opera sempre em ambientes onde a incerteza
impera, principalmente quando o sistema envolve, pela sua natureza,
ações humanas imprevisíveis ou avarias de máquina.
 Os modelos determinísticos certamente contribuem para a
compreensão, a um nível básico, do comportamento dinâmico de
um sistema.
 No entanto, por não poderem lidar com a incerteza, acabam por ser
insuficientes nos processos de tomada de decisão.
 Assim, recorre-se a Processos Estocásticos como uma forma de tratar
quantitativamente
estes
fenômenos,
aproveitando
certas
características de regularidade que eles apresentam para serem
descritos por modelos probabilísticos.
Pesquisa Operacional II
3
O problema das Probabilidades
 Uma variável aleatória é uma função cujo domínio é o conjunto S de
todos os resultados possíveis, e cuja imagem ou contradomínio é o
subconjunto [0,1] dos reais.
 O objetivo das probabilidades é calcular P(A), a probabilidade de
ocorrência de um evento A, que é um subconjunto do espaço amostral
S.
Pesquisa Operacional II
4
Representação Gráfica
Função de
probabilidades
Espaço
amostral
1
X(s)
f
0
S
Pesquisa Operacional II
5
...
 A representação gráfica anterior mostra que as variáveis aleatórias
modelam um sistema particular em um instante de tempo
determinado.
Isto significa que as variáveis
aleatórias não permitem avaliar
o comportamento aleatório de
um sistema em função do tempo.
Pesquisa Operacional II
6
Definição de Processo Estocástico
 Um Processo Estocástico (em inglês, “Stochastic Process” ou “Random
Process” é um conjunto de variáveis aleatórias Xi, onde i pertence a um
espaço amostral S, indexadas a uma variável t que toma valores de um
conjunto T. Esta variável é geralmente a variável tempo.
Xi( t )
i  S ; t T
 Estabelecendo o paralelismo com o caso determinístico, onde uma
função f(t) toma valores bem definidos ao longo do tempo, um
processo estocástico toma valores aleatórios ao longo do tempo.
Um processo estocástico
é uma função que varia
aleatoriamente.
Pesquisa Operacional II
7
Definição de Processo Estocástico
 Aos valores que Xi(t) ou X(t) podem assumir chamam-se estados e ao
seu conjunto X espaço de estados.
 Como exemplo de processos estocásticos, poderemos considerar:
a) X(t) representa o estado de uma máquina (ligada ou desligada) no
momento t.
b) X(t) representa o numero de clientes numa loja no instante t.
c) X(t) representa o número de máquinas avariadas no fim do dia t.
d) X(t) representa a cotação de uma ação no fim do dia t.
e) X(t) representa o nível de estoque de um determinado produto no fim
do dia t.
f) X(t) representa a condição de funcionamento de um componente no
instante t.
Pesquisa Operacional II
8
Definição de Processo Estocástico
 Nos exemplos apresentados, há casos em que o tempo é considerado de
forma discreta (... no fim do dia t) e outros em que é tomado de modo
contínuo (... no momento t).
 A variável tempo é, por definição, uma variável contínua, a qual pode ser
“discretizada” se os fenômenos forem observados a intervalos regulares.
 Outra constatação que se pode fazer é que os “estados” podem ser valores
que a variável X(t) pode assumir (número de clientes, número de
máquinas, etc) como também podem ser estados (máquina avariada, a
funcionar, etc).
Pesquisa Operacional II
9
Representação Gráfica do comportamento estocástico
de um sistema em função do tempo (Proc. Estocástico)
P(x)
1
para cada
P(x) instante em que se
espaço
amostral
analisaO o
experimento,
Xn(t)se
pode
distinguir
associado
aum
cadaespaço
As
probabilidades
associadas
1
amostral
associado
a uma
observação
podepodem
variar.
a cada
experimento
distribuição
de probabilidade
ter varias distribuições
ao
(variável
aleatória).
longo do tempo.
P(x)
1
tempo
Espaço
amostral 1
Espaço
Amostral 2
Espaço
Amostral n
Pesquisa Operacional II
10
Representação Gráfica
X s1 t 
s1
X s2 t 
s2
s3
X s3 t 
S
Pesquisa Operacional II
11
Representação Gráfica
Da representação gráfica anterior pode-se observar que:
 Um processo estocástico é uma família de variáveis aleatórias, ou seja,
para cada instante diferente se deve especificar:
 Os possíveis estados do processo (espaço de estado para esse instante).
 A distribuição de probabilidades que tem associado esse espaço amostral
naquele instante.
 Note-se que:
 O espaço amostral associado ao sistema pode variar (ou não) de instante a
instante.
 As probabilidades associadas a cada resultado pode variar ao longo do tempo.
Pesquisa Operacional II
12
Processo Estocástico
 A partir da representação gráfica anterior, se obtem, de maneira mais
formal:
Definição: Um Processo Estocástico é uma família de
variáveis aleatórias Xi, com i  S,
parametrizadas por outra variável t que
toma valores de um conjunto T. Esta
variável é o tempo.
X i t  com i  S  t T
Pesquisa Operacional II
13
Processo Estocástico
 Um processo estocástico depende de 3 características:
 O espaço de estado, S.
 O parâmetro temporal, T.
 A relação de dependência entre as variáveis aleatórias que o
conformam, Xi(t) (a dinâmica do sistema).
Pt0(x)
Pt1(x)
Ptn(x)
1
1
1
tempo
Pesquisa Operacional II
14
Tipos de Processos Estocásticos
 De acordo ao tipo de espaço de estados os processos estocásticos se podem
classificar em:
 Processos Estocásticos de espaço discreto, se X for um conjunto de
estados finito ou contável (X={0, 1, 2, ...}), como é usualmente referido
uma “cadeia”.
 Processos Estocásticos de espaço contínuo, para qualquer outro
caso.
S
Processos Estocásticos
de espaço discreto
Procesos
Estocásticos
Processos Estocásticos
de espaço contínuo
Pesquisa Operacional II
15
Tipos de Processos Estocásticos
 Também se pode utilizar o parâmetro temporal para classificá-los:
 Processos Estocásticos de parâmetro discreto, se o conjunto T, que
especifica os valores da variável t, for finito ou contável. A notação
usada é {X(t), t=0,1,2,..}. Neste caso, T é normalmente o conjunto dos
inteiros não-negativos.
 Processos Estocásticos de parâmetro contínuo, quando estão
definidos para qualquer instante sendo usada a notação {X(t), t0}
Processos Estocásticos
de parâmetro contínuo
t
Processos
Estocásticos
Processos Estocásticos
de parâmetro discreto
Pesquisa Operacional II
16
Tipos de Processos Estocásticos
Considerando que tanto o tipo de espaço de estados como o tipo de
parâmetro temporal, existem 4 tipos de processos estocásticos:
 Processo de espaço discreto e parâmetro discreto.
 Processo de espaço discreto e parâmetro contínuo.
 Processo de espaço contínuo e parâmetro discreto.
 Processo de espaço contínuo e parâmetro contínuo.
Pesquisa Operacional II
17
Tipos de Processos Estocásticos
S
Processos Estocásticos
de parâmetro contínuo
e espaço discreto
Processos Estocásticos
de parâmetro contínuo
e espaço contínuo
Processos
Estocásticos
t
Processos Estocásticos
de parâmetro discreto
e espaço discreto
Processos Estocásticos
de parâmetro discreto
e espaço contínuo
Pesquisa Operacional II
18
Tipos de Processos Estocásticos
Espaço Discreto e
Parâmetro Discreto
Descrição Geral
Exemplo de um Sistema
Modelagem do Sistema
Representação Gráfica
Pesquisa Operacional II
19
Espaço Discreto e Parâmetro Discreto
Descrição Geral
1-
X s t 
• Neste tipo de processos o parâmetro
toma valores inteiros, pelo que se
associa geralmente aos naturais.
• No caso do espaço discreto, os
resultados são distinguíveis dentro do
espaço.
• A solução deste tipo de processos
consiste em avaliar a probabilidade de
que o sistema se encontre em um
determinado estado justo depois de n
unidades de tempo.
Pesquisa Operacional II
20
Espaço Discreto e Parâmetro Discreto
Exemplo
O sistema que se descreve a continuação pode ser modelado como
um processo estocástico de espaço discreto e parâmetro discreto.
Um jogador vá ao cassino a jogar Black Jack.
Seu capital inicial é de $10.000 em fichas.
Em cada aposta pode ganhar ou perder $1.000
O máximo de dinheiro que pode acumular o
jogador antes de que o cassino quebre é “ C ”.
• Se deseja conhecer o capital acumulado pelo
jogador depois de n apostas, n >= 1.
•
•
•
•
Pesquisa Operacional II
21
Espaço Discreto e Parâmetro Discreto
Modelagem formal do sistema
Seja n o número de aposta que se pode fazer. Isto corresponde ao
parâmetro temporal.
n = 0, 1, 2, 3,......,k
O espaço de estados está definido pelas possíveis quantidades de
dinheiro que pode possuir o jogador em n.
S= { 0, 1.000, 2.000...., C }
Resolver este processo estocástico consiste em avaliar:
P(X(n)=i) = pi(n),
a probabilidade de que o jogador tenha i quantidade de dinheiro
justo depois da n-ésima aposta.
Pesquisa Operacional II
22
Espaço Discreto e Parâmetro Discreto
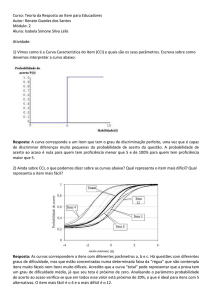
Representação Gráfica do sistema modelado
O jogador
S
começa
com
13000
$10000.
Espaço de estados possíveis
para as três primeiras apostas.
Representa a quantidade de
dinheiro acumulada pelo jogador
justo depois da n-ésima aposta.
12000
11000
10000
9000
8000
7000
1
2
3
Pesquisa Operacional II
n
23
Tipos de Processos Estocásticos
Espaço Discreto e
Parâmetro Discreto
Espaço Contínuo
e
Parâmetro Discreto
Descrição Geral
Exemplo de um sistema
Modelagem do sistema
Representação gráfica
Pesquisa Operacional II
24
Espaço Contínuo e Parâmetro Discreto
Descrição Geral
1-
X s t 
• Neste tipo de processos o parâmetro
toma valores inteiros, pelo que se
associa geralmente aos naturais.
• No caso do espaço contínuo,
resultados
estão
associados
intervalos de espaço.
os
a
• A informação que se obtém a partir
deste tipo de processos é a
probabilidade acumulada dentro de um
intervalo do espaço de estados logo de
n experimentos.
Pesquisa Operacional II
25
Espaço Contínuo e Parâmetro Discreto
Exemplo
O sistema que se descreve a continuação pode ser modelado como
um processo estocástico de espaço contínuo e parâmetro discreto.
• O experimento consiste em tomar o tempo que
demora um pacote ao ser enviado e recebido
através da rede por um mesmo terminal.
• As medições são realizadas cada vez que se envia
um pacote desde o equipamento transmissor.
• O tempo varia continuamente desde um mínimo
tempo de propagação “m” até o timeout “M”.
Pesquisa Operacional II
26
Espaço Contínuo e Parâmetro Discreto
Modelagem formal do sistema
Seja n o número de experimento que se realiza, enviar e receber
um pacote. Isto define o parâmetro temporal.
n = 0, 1, 2, 3,......,k
O espaço de estados está definido por todos os possíveis tempos
medidos em cada experimento.
S= [ m, M ]
A solução deste exemplo esta descrita por, seja:
P(T(n)=i) = pi(n),
a probabilidade de que o tempo medido no n-ésimo experimento
seja i.
Pesquisa Operacional II
27
Espaço Contínuo e Parâmetro Discreto
Representação Gráfica do sistema modelado
P(t)
P(t)
Probabilidade
1
de que um
pacote
demore no
máximo i.
1
0
P(t)
0
m1
2
3
4
m
1
Distribuição de
probabilidade
para o
experimento N
0
n
N
m
i
M
Espaço
Amostral 1
M
Espaço
Amostral 2
M
Espaço
Amostral n
Pesquisa Operacional II
28
Tipos de Processos Estocásticos
Espaço Discreto y
Parâmetro Discreto
Espaço
Contínuo
y
Parâmetro Discreto
Descrição Geral
Descrição de um sistema
Espaço Discreto y
Parâmetro Contínuo
Pesquisa Operacional II
Modelagem do sistema
Representação gráfica
29
Espaço Discreto e Parâmetro Contínuo
Descrição Geral
1-
X s t 
• Neste tipo de processos o parâmetro
toma valores dentro de um intervalo
contínuo, pelo que se associa
geralmente ao tempo.
• No caso do espaço discreto, os
resultados associados a cada estado
são totalmente distinguíveis dentro do
espaço.
• A informação que se obtém a partir
deste tipo de processos é a
probabilidade de estar em um estado
determinado logo de um intervalo de
tempo.
Pesquisa Operacional II
30
Espaço Discreto e Parâmetro Contínuo
Exemplo
O sistema que se descreve a continuação pode ser modelado como
um processo estocástico de espaço discreto e parâmetro contínuo.
• Com um sistema digital se registra em forma
contínua a utilização de um canal de dados.
• O parâmetro temporal é contínuo pelo tipo de
medição, porém o espaço é discreto porque o
canal pode ter utilizado um número determinado
de bits em cada unidade de tempo.
Pesquisa Operacional II
Central
Telefônica
31
Espaço Discreto e Parâmetro Contínuo
Modelagem formal do sistema
Seja t o parâmetro temporal que define o tempo transcorrido em
uma medição.
t = [0, [
O espaço de estados está definido pela quantidade de bits por
unidade de tempo.
S= { 0, 1, 2, 3, 4, 5, …, C }
A solução deste exemplo esta descrita por, seja:
P(T(t)=i) = pi(t),
a probabilidade de que ao ter transcorrido t segundos tenham
transitado i bits pelo canal de dados.
Pesquisa Operacional II
32
Espaço Discreto e Parâmetro Contínuo
Representação Gráfica do sistema modelado
P(t)
1
1
0
2
Probabilidade de que
depois de t segundos
tenham transitado 1 bit.
t
Medição do
trafego de bits.
Espaço
Amostral
Pesquisa Operacional II
33
Tipos de Processos Estocásticos
Espaço Discreto y
Parâmetro Discreto
Espaço
Contínuo
y
Parâmetro Discreto
Descrição Geral
Descrição de um sistema
Modelagem do sistema
Espaço Discreto y
Parâmetro Contínuo
Espaço
Contínuo
y
Parâmetro Contínuo
Pesquisa Operacional II
34
Espaço Contínuo e Parâmetro Contínuo
Descrição Geral
1-
X s t 
• Neste tipo de processos o parâmetro
toma valores dentro de um intervalo
contínuo, pelo que se associa
geralmente ao tempo.
• No caso do espaço contínuo,
resultados
estão
associados
intervalos de espaço.
os
a
• A informação que se obtém a partir
deste tipo de processos é a
probabilidade de acumular certa
quantidade logo de um intervalo de
tempo.
Pesquisa Operacional II
35
Espaço Contínuo e Parâmetro Contínuo
Exemplo
O sistema que se descreve a continuação pode ser modelado como
um processo estocástico de espaço contínuo e parâmetro contínuo.
• Um exemplo de isto é o Movimento Browniano que
descreve o movimento de uma partícula em um meio
aquoso.
• Seja X(t) a posição X da partícula no instante de
tempo t. Logo de um intervalo de tempo a partícula
se encontrará em alguma posição aleatória. O
problema é encontrar a probabilidade de que a
partícula se encontre em qualquer posição X para
qualquer instante de tempo t.
Pesquisa Operacional II
36
Espaço Contínuo e Parâmetro Contínuo
Modelagem formal do sistema
Seja t o parâmetro temporal:
t = [0, [
O espaço de estados está definido por todas as possíveis posições
da partícula no meio aquoso.
X= ] -, + [
A solução deste exemplo esta descrita por, seja:
P(X(t)=i) = pi(t),
a probabilidade de encontrar a partícula na posição i no instante t.
Pesquisa Operacional II
37
Características Estatísticas das Variáveis Aleatórias
 Um processo estocástico diz-se estacionário se o seu comportamento
estocástico for independente do tempo, ou seja, se a função distribuição
da(s) v.a. que o define(m) não variar no tempo.
 Um processo estocástico diz-se Markoviano ou de Markov se for
estacionário e gozar da propriedade de Markov ou da “perda de memória”,
isto é, se o seu comportamento futuro apenas for condicionado pelo
estado presente, independentemente do seu histórico ou dos estados
visitados no passado. A única distribuição contínua que apresenta esta
propriedade é a distribuição exponencial.
Para um processo de Markov é completamente
irrelevante qualquer informação sobre estados
passados ou sobre o tempo de permanência no
estado presente.
Pesquisa Operacional II
38
Características Estatísticas das Variáveis Aleatórias
 Num processo estocástico as transições entre estados são causadas pela
ocorrência de acontecimentos ou eventos, pelo que a variável aleatória
(diretamente restringida pela propriedade de ausência de memória) é o
tempo entre acontecimentos sucessivos.
 Um processo estocástico de Semi-Markov é uma generalização de um
processo de Markov, já que, para aquele, a informação sobre o tempo de
permanência no estado atual deixa de ser irrelevante; contudo, continua a
ser irrelevante para o comportamento futuro qualquer informação sobre
os estados visitados no passado.
 A conseqüência é que os tempos entre acontecimentos sucessivos deixam
de estar “restringidos” à distribuição exponencial, podendo seguir
qualquer distribuição de probabilidade.
Pesquisa Operacional II
39
Características Estatísticas das Variáveis Aleatórias
Apesar da propriedade de Markov nem
sempre ter aderência à realidade, os
processos de Markov são, de longe, os
processos estocásticos mais utilizados graças
à sua facilidade de tratamento.
Pesquisa Operacional II
40