Slide 1 - Moodle

Distribuições Contínuas
de Probabilidade
Objetivos

Apresentar a Distribuição de Probabilidade
Normal

Resolver problemas de probabilidade que
envolvem a Distribuição Normal

Interpretar o gráfico da Distribuição Normal
Variáveis Aleatórias
Variável
Discreta
Numérica
Categórica
(Quantitativa)
(Qualitativa)
Contínua
Variável Aleatória Contínua

Número inteiro ou fracionário

Obtido por meio de medição

Números infinitos ou valores em intervalos
Variável Aleatória Contínua Exemplos
Experimento
Variável
Aleatória
Possíveis
Valores
Peso de 100 Pessoas Peso
45.1, 78, ...
Horas trabalhadas por dia
Horas
8, 6.5, 7.1,...
Despesa com alimentação
Despesa
54, 42, ...
Medir o tempo entre a Tempo
0, 1.3, 2.78, ...
chegada dos carros
em minutos
Variável Aleatória Contínua Exemplos
Experimento
Operar um banco
Encher uma garrafa de 1 litro
Trabalhar em um projeto
Variável
Aleatória
Possíveis
Valores
Tempo
X≥0
Nº de ml
0≤x≤1
% do término 0 ≤ x ≤ 100%
Função de Densidade de
Probabilidade

Fórmula Matemática

Mostra todos os valores, X,
e as Freqüências, f(X)


f(X) Não é Probabilidade
Freqüência
(Valor, Freqüência)
f(X)
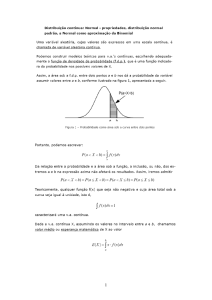
Propriedades
∫ f ( X )dx = 1
(área sob a curva)
f (X )  0 a  X  b
a
b
Valor
X
Probabilidade de uma V.A.
Contínua
Probabilidade é a
área sob a curva!
P (c  X  d ) =
∫c f ( X ) dx
d
f(X)
a
© 1984-1994 T/Maker Co.
c
d
b
X
Modelos de Distribuição
Contínua
Distribuição
Contínua de
Probabilidade
Normal
Outras
Desafio…
O valor sacado diariamente de
um caixa eletrônico tem
distribuição Normal com média
de R$50.000 e desvio-padrão de
R$10.000).
Quanto em dinheiro o caixa
deverá ter, por dia, para que a
probabilidade de faltar dinheiro
seja menor do que 5%?
Importância da Distribuição
Normal

Descrição de vários processos e fenômenos

Pode ser usada para aproximar algumas
distribuições discretas

É a base da Inferência Estatística
Distribuição Normal

Forma de ‘Sino’ –
Simétrica

Média = Moda =
Mediana
f(X)
X
Média
Moda
Mediana
Distribuição Normal

Média ()

Desvio-Padrão ()

- 


+
X
Distribuição Normal
Função de Densidade
f (X ) =
f(X)
p
 x
X
x
=
=
=
=
=
-
1
2 p x
2
e
1 X - x 2
[
2
x
]
função de densidade da Normal
3.14159; e = 2.71828
desvio-padrão populacional
valor da variável aleatória (- < X < )
média populacional
Efeito da Variação dos
Parâmetros (x & x)
f(X)
B
A
C
X
Probabilidade
Distribuição Normal
Probabilidade é
a área sob a
curva!
∫c f ( X ) dx ?
P (c  X  d ) =
f(X)
c
d
X
d
Tabela de Distibuição Normal
As Distribuições diferem na
média e no desvio-padrão.
Seria necessário uma tabela
para cada distribuição.
f(X)
X
Infinitas Tabelas!
Distribuição Normal Padronizada
Z=
Distribuição
Normal
X
X - x
x
Distribuição Normal
Padronizada
z = 1
X
X
Z = 0
Uma Tabela!
Z
Padronização de dados

Cálculo da probabilidade: usa-se a distribuição
padronizada, com média zero e desvio padrão 1.

Padronizando valores:
 Deslocar o valor da média para zero.
 Mudar a escala, dividindo os valores pelo desvio
padrão, que passa a ser 1.
x

Z=

onde X é N( ; ) e Z é N(0;1)
Exemplo de Padronização
Z=
Distribuição
Normal
X - x
x
X = 10
X= 5 6.2 X
=
6.2 - 5
10
= .12
Distribuição Normal
Padronizada
Z = 1
Z= 0 .12
Z
Encontrando uma Probabilidade
Tabela de Probabilidade
Normal Padronizada
Z
.00
.01
Z = 1
.02
0.0 .0000 .0040 .0080
.0478
0.1 .0398 .0438 .0478
0.2 .0793 .0832 .0871
Z= 0 .12
0.3 .1179 .1217 .1255
Probabilidades
Z
Exemplo
P(3.8  X  5)
Z=
X - x
x
Distribuição
Normal
=
3.8 - 5
10
= -.12
Distribuição Normal
Padronizada
X = 10
Z = 1
.0478
3.8 X= 5
X
-.12 Z= 0
Z
Exemplo
P(2.9  X  7.1)
Distribuição
Normal
X -  x 2.9 - 5
Z=
=
= -.21
10
x
X -  x 7.1 - 5
Z=
=
= .21
10
x
X = 10
Distribuição
Normal
Padronizada
Z = 1
.1664
.0832 .0832
2.9 5 7.1 X
-.21 0 .21
Z
Exemplo
P(X  8)
Z=
X - x
x
Distribuição
Normal
=
8-5
10
= .30
Distribuição Normal
Padronizada
X = 10
Z = 1
.5000
.3821
.1179
X= 5
8
X
Z= 0 .30 Z
Exemplo
P(7.1  X  8)
Distribuição
Normal
X -  x 7.1 - 5
Z=
=
= .21
10
x
X - x 8 - 5
Z=
=
= .30
10
x
X = 10
Distribuição
Normal
Padronizada
Z = 1
.1179
.0347
.0832
x = 5
7.1 8
X
z = 0
.21 .30 Z
Desafio…
Você trabalha no setor de Controle
de Qualidade da GE. A vida útil de
uma lâmpada tem Distribuição
Normal com mx= 2000 horas &
sx=200 horas. Qual é a
probabilidade de uma lâmpada durar:


entre 2000 & 2400
horas?
Menos de 1470 horas?
Consultando a Tabela da Normal
Tabela da distribuição Normal
Padronizada
Qual é o Z dado
P(Z) = .1217?
.1217
Z = 1
Z
.00
.01
0.2
0.0 .0000 .0040 .0080
0.1 .0398 .0438 .0478
Z= 0 .31
Z
0.2 .0793 .0832 .0871
0.3 .1179 .1217 .1255
Achando um Valor X para uma
Probabilidade Conhecida
Distribuição Normal
Padronizada
Distribuição Normal
X = 10
Z = 1
.1217
X= 5
?
X
.1217
Z= 0 .31
X =  x + Z   x = 5 + .31 10 = 8.1
Z
Áreas sob a curva para a
distribuição Normal
x-3
-2
-1x
 +1
68,26%
95,44%
???
+3
+2
`X