cgslide7

Curvas e Superfícies
Alex F. V. Machado
[email protected]
Importância das Curvas
•
•
•
na engenharia, projeto e manufatura de uma ampla
gama de produtos, como automóveis, cascos de navios,
fuselagem e asas de aviões, lâminas de propulsão,
sapatos, garrafas, edificações, etc.
na descrição e interpretação de fenômenos físicos em
áreas como geologia, física e medicina.
Em sistemas CAD que incorpora modelos matemáticos e
computacionais desenvolvidos para apoiar os processos
de engenharia, projeto e manufatura.
Superfícies
• Frequentemente, superfícies são descritas por uma
malha de curvas definidas em planos ortogonais.
• As curvas podem ser obtidas através da digitalização de
um modelo físico ou desenho, e posterior ajuste de uma
curva matemática aos pontos digitalizados.
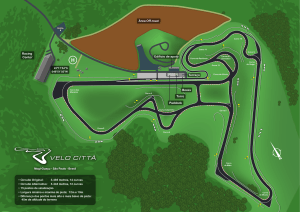
Interpolação e Aproximação
Uma curva baseada em
interpolação intercepta os
pontos de controle.
Uma curva baseada em
aproximação sempre
intercepta os pontos finais.
Os pontos de controle servem
para modelar a curva.
• Interpolação: Hermite, Catmull-Rom spline
• Aproximação: Bézier, curvas B-spline
Curvas de Hermite
• Formada por 2 pontos e 2 vetores tomados
como tangentes à curva nos pontos
• Passa pelos 2 pontos especificados
Curvas de Bézier
• A curva de Bézier é definida pela equação:
• Onde P é o ponto de controle e B é a função
de blending
Curvas de Bézier
• Curva de Bézier Linear
Curvas de Bézier
• Curva de Bézier Quadrática
Curvas de Bézier
• Curva de Bézier Cúbica
Curvas de Bézier
• Construindo curvas de Bézier
The t in the function for a linear Bézier curve can be thought of as
describing how far B(t) is from P0 to P1. For example when t=0.25,
B(t) is one quarter of the way from point P0 to P1. As t varies from
0 to 1, B(t) describes a curved line from P0 to P1.
Curvas de Bézier
• Construindo curvas de Bézier
For higher-order curves one needs correspondingly more
intermediate points. For cubic curves one can construct
intermediate points Q0, Q1 & Q2 that describe linear Bézier
curves, and points R0 & R1 that describe quadratic Bézier curves.
B-Splines
• Na síntese de imagens uma curva pode possuir formas
muito complexas para serem representadas por simples
curvas cúbicas de Bézier.
• Aumentando o grau da curva de Bézier será aumentado
proporcionalmente a flexibilidade da forma projetada.
• Este fato no entanto aumenta consideravelmente o
processamento e o gasto de memória.
• Por essas razões é divido a curva em “sub-curvas” que
podem ser representadas por equações de menores
graus.
• Uma curva que é constituída de diversas “sub-curvas”
de Bézier, quer dizer, uma composição de curvas de
Bézier, é chamada de B-Splines.
B-Splines
NURBS
(Non-uniform rational B-spline)
• É um modelo matemático usado regularmente em programas
gráficos para gerar e representar curvas e superficies.
• É baseado na B-Spline
NURBS
(Non-uniform rational B-spline)