Velocidade média no intervalo (t0, t1) - MTM

A integral definida
Prof. Méricles Thadeu Moretti
MTM/CFM/UFSC.
4 - INTEGRAL DEFINIDA - CÁLCULO DE ÁREA
Já vimos como calcular a área de um tipo bem específico de região para algumas
funções no intervalo [0, t]. O Segundo Teorema Fundamental do Cálculo estabelece
uma relação que nos permitirá calcular a área em um intervalo qualquer.
Resultado_5: Segundo Teorema Fundamental do Cálculo
Seja f é contínua em um intervalo fechado I. Se P é derivável no intervalo aberto I e
P´(x) = f(x), então para cada a, b em I:
b
 f (x)dx  P(x)
b
a
 P(b)  P(a)
a
a é o limite inferior de integração e b o superior, f(x) é o integrando. Esta integral é
chamada Integral de Newton [4, p.255].
1
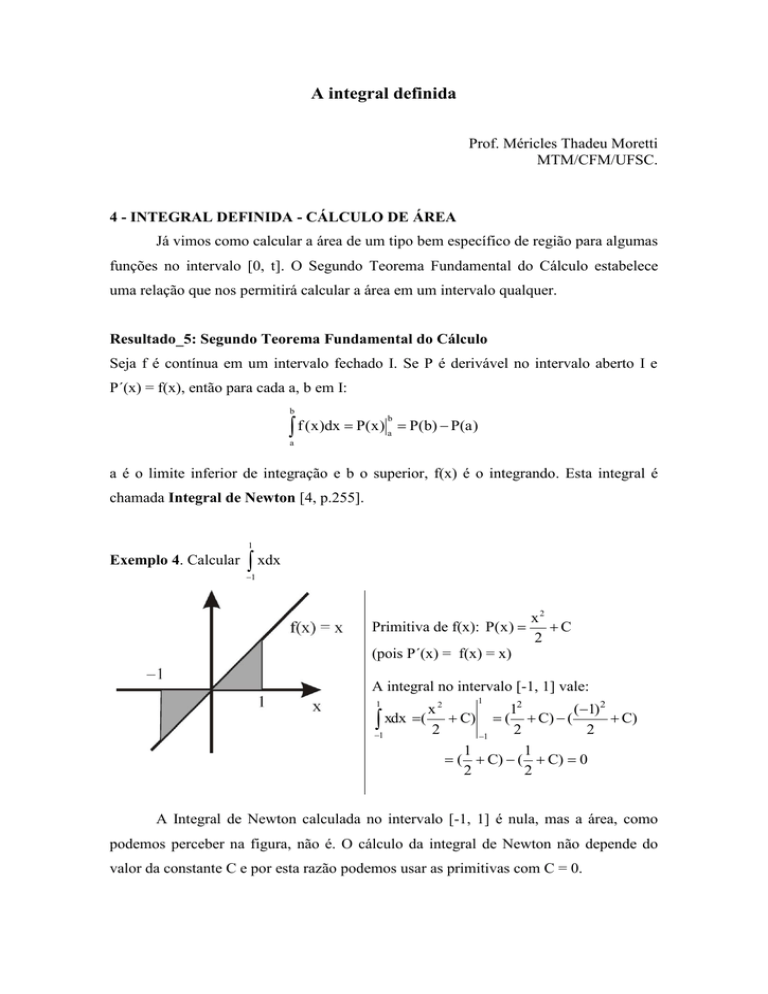
Exemplo 4. Calcular
 xdx
1
Primitiva de f(x): P(x) 
x2
C
2
(pois P´(x) = f(x) = x)
A integral no intervalo [-1, 1] vale:
1
x2
12
(1)2
 xdx ( 2  C)  ( 2  C)  ( 2  C)
1
1
1
1
1
 (  C)  (  C)  0
2
2
A Integral de Newton calculada no intervalo [-1, 1] é nula, mas a área, como
podemos perceber na figura, não é. O cálculo da integral de Newton não depende do
valor da constante C e por esta razão podemos usar as primitivas com C = 0.
4.1 – Propriedades da Integral de Newton
As integrais de Newton gozam das seguintes propriedades
P1.
P.2
P.3
b
b
b
a
a
a
 [f (x)  g(x)]dx   f (x)dx   g(x)dx
b
b
a
a
 kf (x)dx  k  f (x)dx, k constante.
c
b
c
a
a
b
 f (x)dx   f (x)dx   f (x)dx, a  b  c .
4.2 - Cálculo de área
Indicamos a seguir como calcular a área de uma região mostrada na figura a
seguir.
Sejam f e g integráveis no intervalo [a, b]. A área
entre as curvas f e g neste intervalo vale (em
unidades de área):
b
A(a, b) =  [(g(x)  f (x)]dx
a
Observamos que A(a, b) ≥ 0 e A(a, a) = 0, estas são características importantes
que devem ter a primitiva para o cálculo da área. É preciso ter cuidado com os limites
de integração e com o sinal da função no integrando que deve ser sempre positiva no
intervalo de integração considerado.
Para o Exemplo 4, a área da região hachurada (entre f(x) = x e y = 0 no intervalo
[-1, 1]) pode ser calculada da seguinte maneira (em unidades de área):
0
1
0
1
x2
x2
1 1
Área =  (0  x)dx   (x  0)dx  (  C1 )  (  C2 )    1 .
2
2
2 2
1
0
1
0
EXEMPLOS 4.2
4.2.1) Calcular a área da região limitada pelas curvas y = x2 e y = 4.
Pontos de encontro entre y = x2 e y = 4:
x2 = 4
 x2 - 4 = 0
 (x - 2)(x + 2) = 0
 x = 2 ou x = -2
Cálculo em unidades de área:
2
2
x3
A(-2, 2) =  [4  x ]dx  (4x  )
3 2
2
2
8
8
32
 (8  )  (8 
)
3
3
3
4.2.2) Usando a idéia de elementos de área, calcular a área da região limitada pelas
curvas
y = x2 e y = 4.
Resolução
O elemento de área dA é a área de
um retângulo de dimensões (4 - x2) e
dx:
dA = (4 - x2)dx
Integrando de [-2, 2], tem-se:
2
2
2
2
2
 dA   (4  x )dx
2
A(2, 2)   (4  x 2 )dx
2
Já calculada anteriormente e vale:
A(2, 2) 
32
unid. de área
3
4.2.3) Calcular a área limitada pela parábola y2 = 4x e a reta y = 2x - 4.
a) Resolução com elemento de área vertical
Os pontos de encontro entre y2 = 4x e y = 2x - 4 (já assinalados no gráfico) são:
4x = (2x - 4)2  x2 - 5x + 4 = 0  x = 1 ou x = 4. Os pontos são (1, -2) e (4, 4).
Cálculo da área (em unidades de área):
1
4
Área =  [(2 x  (2 x )]dx   [(2 x  (2x  4)]dx
0
1
1
4
Área =  4 x dx   (2 x  2x  4)dx
0
8
Área  x
3
1
3 1
2
0
3
4
4
 ( x 2  x 2  4x )
3
1
8 19
Área  
9
3 3
b) Resolução com elemento de área horizontal
Observar que y2 = 4x 
1 2
1
y  x e que y = 2x - 4  y  2  x
4
2
Cálculo da área (em unidades de área):
4
4
1
1
y2
y3
Área   ( y  2  y 2 )dy  (  2 y  )  9
2
4
4
12 2
2
Na resolução em (a) foram necessários elementos de área distintos enquanto que
na resolução em (b) apenas um e tal resolução mostrou-se ser mais simples.
mm´
(, m e m´ constantes positivas) e as retas
r2
verticais r = a e r = b (b > a > 0 constantes reais).
4.2.4) Calcular a área limitada por F  
Resolução.
Considere o desenho a seguir.
Tem-se, em unidades de área:
b
b
a
a
b
dr
mm´

2
r
r
 dA   
 A  mm´ 
a
mm´
.dr
r2
b
a
1 1
 mm´(  )
a b
Se considerarmos que F representa a força gravitacional que atrai dois corpos de
massas m e m´,  uma constante de proporcionalidade que depende das unidades
utilizadas nas outras grandezas e r a distância que separa esses corpos, o que acabamos
de calcular é o trabalho exigido para que uma das massas passe da posição r = a para a
posição r = b.
4.2.5) Encontrar a área da região limitada pelas curvas y = x + 6, y = x3 e y = -x/2.
Resolução.
 Ponto de encontro entre y = x + 6 e y = x3:
x3 = x + 6  x3 - x - 6 = 0. Possibilidades de raízes: {1, 2, 3, 6}
Substituindo esses valores na equação x3 - x - 6 = 0, verificamos que x = 2 é raiz
(verifique que x = 2 é a única raiz real). Essas curvas se cruzam no ponto (2, 8).
 Ponto de encontro entre y = -x/2 e y = x3:
x3 = -x/2 + 6  2x3 + x = 0  x(2x2 + 1) = 0  x = 0 ou 2x2 + 1 = 0.
x = 0 é a única raiz real. Essas curvas se cruzam no ponto (0, 0)
 Ponto de encontro entre y = x + 6 e y = -x/2
x + 6 = -x/2  x = -4. Essas curvas se cruzam no ponto (-4, 2).
Gráfico das curvas
O cálculo da área em unidades de área vale:
0
2
x
A   [(6  x )  ( )].dx   [(6  x )  x 3 ].dx
2
4
0
0
A   (6 
4
2
3x
).dx   (6  x  x 3 ).dx
2
0
0
2
3x 2
x2 x4
A  (6 x 
)  (6 x 
 )
4 4
2
4 0
A = 12 + 10 = 22
Exercícios: a) Calcular esta mesma área usando elementos de área verticais.
b) Calcular a área da região limitada por y = -x/2, y = x3 e x = 2. (Resp. 5 unid. de área).
4.2.6) Encontrar a área da região limitada pelas curvas y = 2x, y = 2-x e y = 4.
Resolução.
Ponto de encontro entre y = 2x e y = 4: x = 2;
Ponto de encontro entre y = 2-x e y = 4: x = -2;
Ponto de encontro entre y = 2x e y = 2-x: x = 0.
Gráfico das curvas
O cálculo de área em unidade de área vale:
0
2
2
0
A   (4  2  x ).dx   (4  2 x ).dx
0
2
2x
2x
A(
 4x )  (4x 
)
ln 2
ln 2 0
2
A  (8 
3
3
)  (8 
)
ln 2
ln 2
A  2(8 
3
)  7,34
ln 2
Exercícios. a) Resolver este mesmo problema usando elemento de área vertical.
b) Calcular a área entre as curvas y = 2x e y = 2-x no intervalo [-2, 0].
(Resp.
9
Unid. de área)
4 ln 2
Bibliografia
[1] ANTAR NETO, A. et Alli. Introdução à Análise Matemática. São Paulo: Editora
Moderna, 1985.
[2] FLEMMING, D. M. & GONÇALVES, M. B. Cálculo "A". Florianópolis: Editora da
UFSC, 1992.
[3] GUIDORIZZI, H. L. Um Curso de Cálculo. (Volume 1, 2ª Edição). Rio de Janeiro:
LCT, 1985.
[4] KITCHEN JR., Joseph W. Calculus of one variable. Massachusetts: AddinsonWesley, 1968.
[5] KUELKAMP, Nilo; Cálculo I, Florianópolis: Editora da UFSC.